Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học Ôn tập chương III – Phương pháp tọa độ trong mặt phẳng

Bài 10 trang 119 SGK Hình học 10 nâng cao


Tìm tọa độ các tiêu điểm của (E) và (H)

Lựa chọn câu để xem lời giải nhanh hơn

Cho \((E):{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1\) và hypebol \((H):{{{x^2}} \over 5} - {{{y^2}} \over 4} = 1.\)

LG a

Tìm tọa độ các tiêu điểm của (E) và (H).

Lời giải chi tiết:

Với \((E):{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1\) ta có:

\({a^2} = 5,{b^2} = 4\) \(\Rightarrow a = \sqrt 5 ,b = 2\)

\(\Rightarrow \,c = \sqrt {{a^2} - {b^2}}  = 1\)

Tọa độ các tiêu điểm của (E) là \({F_1}( - 1\,;\,0)\,,\,\,{F_2}(1\,;\,0)\)

Với (H) : \({{{x^2}} \over 5} - {{{y^2}} \over 4} = 1\) , ta có:

\({a^2} = 5,{b^2} = 4\) \(\Rightarrow a = \sqrt 5 ,b = 2\)

\(\Rightarrow \,c = \sqrt {{a^2} + {b^2}}  = 3\)

Tọa độ các tiêu điểm của (H) là \({F_1'}( - 3\,;\,0)\,,\,\,{F_2'}(3\,;\,0)\)

LG b

Vẽ phác elip (E) và hypebol (H) trong cùng một hệ trục tọa độ.

Lời giải chi tiết:

Vẽ (E) và (H).

 

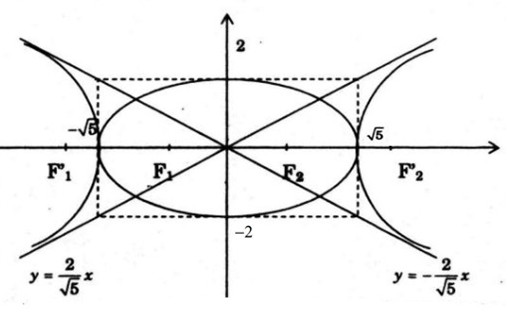
(E ) nhận Ox, Oy làm hai trục đối xứng

\({F_1}( - 1\,;\,0)\,,\,\,{F_2}(1\,;\,0)\) làm tiêu điểm

Cắt Ox tại \(\left( { - \sqrt 5 ;0} \right),\left( {\sqrt 5 ;0} \right)\) và cắt Oy tại \(\left( {0; - 2} \right),\left( {0;2} \right)\)

(H) nhận \({F_1'}( - 3\,;\,0)\,,\,\,{F_2'}(3\,;\,0)\) làm tiêu điểm, trục Ox, Oy là trục đối xứng

Các đường thẳng \(y =  \pm \frac{2}{{\sqrt 5 }}x\) là tiệm cận.

LG c

Tìm tọa độ các giao điểm của (E) và (H).

Lời giải chi tiết:

Tọa độ giao điểm của (E) và (H) là nghiệm của hệ phương trình

\(\left\{ \matrix{
{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1 \hfill \cr 
{{{x^2}} \over 5} - {{{y^2}} \over 4} = 1 \hfill \cr} \right.\) \(\Leftrightarrow \,\,\,\left\{ \matrix{
{x^2} = 5 \hfill \cr 
{y^2} = 0 \hfill \cr} \right.\) \( \Leftrightarrow \,\,\,\left\{ \matrix{
x = \pm \sqrt 5 \hfill \cr 
y = 0 \hfill \cr} \right.\) 

Vậy tọa đô giao điểm của (E) và (H) là \(\left( {\sqrt 5 \,;\,0} \right)\) và \(\left( -{\sqrt 5 \,;\,0} \right)\) .

Loigiaihay.com


Bình chọn:
3.5 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến Lớp 10 tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua