Lý thuyết Mẫu nguyên tử BO
Mẫu nguyên tử Bo bao gồm mô hình hành tinh nguyên tử và hai tiên đề của Bo.
I. NỘI DUNG
1. Mẫu nguyên tử Bo
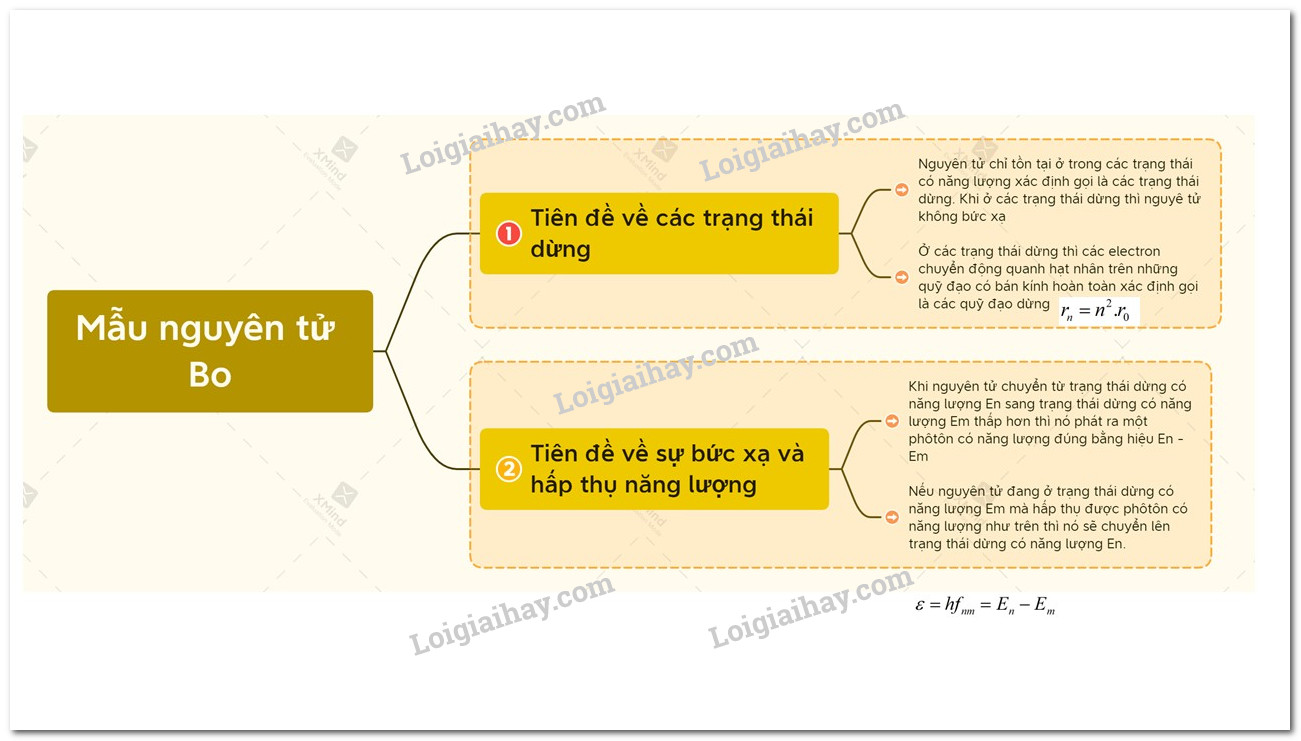
a. Tiên đề về trạng thái dừng
- Nguyên tử chỉ tồn tại trong những trạng thái có năng lượng xác định \({E_n}\) gọi là trạng thái dừng. Khi ở trạng thái dừng năng lượng không bức xạ.
- Bán kính quỹ dạo dừng: \({r_n} = {n^2}{r_0}\)
Trong đó:
- \({r_0}\) - bán kính nguyên tử ở trạng thái cơ bản \(\left( {{r_0} = {\rm{ }}{{5,3.10}^{ - 11}}} \right)\)
- \(n{\rm{ }} = {\rm{ }}1,{\rm{ }}2,{\rm{ }}3{\rm{ }}...\)

- Năng lượng electron trong nguyên tử hiđro: \({E_n} = - \dfrac{{13,6}}{{{n^2}}}eV\) với \(n \in N*\)
b. Tiên đề về sự bức xạ và hấp thụ
- Khi nguyên tử chuyển từ trạng thái dừng có năng lượng \({E_n}\) sang trạng thái có năng lượng \({E_m} < {\rm{ }}{E_n}\) thì nó phát ra một photon có năng lượng \(\varepsilon = {E_n} - {E_m}\).
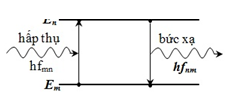
- Ngược lại, nếu nguyên tử ở trạng thái dừng có năng lượng \({E_m}\) mà hấp thụ được một phôtôn có năng lượng hf đúng bằng hiệu \({E_n}--{\rm{ }}{E_m}\) thì nó chuyển sang trạng thái dừng có năng lượng \({E_n}\) lớn hơn.
- Sự chuyển từ trạng thái dừng \({E_m}\) sang trạng thái dừng \({E_n}\) ứng với sự nhảy của electron từ quỹ đạo dừng có bán kính \({r_m}\) sang quỹ đạo dừng có bán kính \({r_n}\) và ngược lại.
2. Quang phổ vạch của nguyên tử Hidrro
- Bình thường electron (e) chỉ chuyển động trên quỹ đạo K (trạng thái cơ bản)
- Khi bị kích thích, e nhảy lên quỹ đạo có năng lượng lớn hơn L, M, N, ... Thời gian ở trạng thái kích thích rất ngắn (10-8s) sau đó e chuyển về các quỹ đạo bên trong và phát ra photon có năng lượng đúng bằng hiệu \(\varepsilon = {E_{cao}} - {E_{thap}}\)
- Mỗi photon tần số f ứng với vạch sáng có bước sóng \(\lambda = \dfrac{c}{f}\) cho 1 vạch quang phổ.
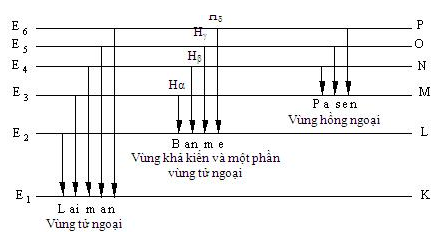
- Quang phổ vạch phát xạ của Hiđro nằm trong 3 dãy (hình trên)
- Dãy Laiman: e chuyển từ trạng thái kích thích \( \to \) quỹ đạo K
- Dãy Banme: e chuyển từ trạng thái kích thích \( \to \) quỹ đạo L
- Dãy Pasen: e chuyển từ trạng thái kích thích \( \to \) quỹ đạo M
Trong dãy Banme, nguyên tử Hiđro có 4 vạch: \({H_\alpha }\) (đỏ), \({H_\beta }\) (lam), \({H_\gamma }\) (chàm), \({H_\delta }\) (tím)
Ở trạng thái cơ bản \({E_1} = {\rm{ }} - 13,6eV,{E_n} = \dfrac{{{E_1}}}{{{n^2}}}\)
II - CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
1. Dạng 1: xác định vận tốc, tần số \(f\) , tốc độ góc \(\omega \) năng lượng của e ở trạng thái dừng thứ n.
Khi e chuyển động trên quỹ đạo n, lực hút tĩnh điện đóng vai trò là lực hướng tâm:
\(\left\{ \begin{array}{l}{F_{ht}} = {F_{CL}} \leftrightarrow \dfrac{{mv_n^2}}{{{r_n}}} = \dfrac{{k{q_1}{q_2}}}{{{r^2}}} = \dfrac{{k{e^2}}}{{{r_n}^2}}\\{r_n} = {n^2}{r_0}\end{array} \right. \to {v_n} = e\sqrt {\dfrac{k}{{{r_n}m}}} = \dfrac{e}{n}\sqrt {\dfrac{k}{{{r_0}m}}} \) với \(k{\rm{ }} = {\rm{ }}{9.10^9}\)
Tần số: \(f = \dfrac{\omega }{{2\pi }} = \dfrac{{{v_n}}}{{2\pi {r_n}}}\)
Năng lượng ở trạng thái dừng bao gồm: thế năng tương tác và động năng của electron:
\(\begin{array}{l}{E_n} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}} = - \dfrac{{k{e^2}}}{{{r_n}}} + \dfrac{{mv_n^2}}{2} = - mv_n^2 + \dfrac{{mv_n^2}}{2} = - \dfrac{{mv_n^2}}{2}\\ \to {v_n} = \sqrt { - \dfrac{{2{E_n}}}{m}} \end{array}\)
Khi e quay trên quỹ dạo dừng thì nó tạo ra dòng điện có cường độ: \(I = \dfrac{q}{t} = \dfrac{{\left| e \right|}}{T}\)
2. Dạng 2: tính bước sóng, tần số của photon hấp thụ hoặc bức xạ và số vạch quang phổ phát ra
\(\varepsilon = hf = \dfrac{{hc}}{\lambda } = {\rm{ }}{E_{cao}} - {\rm{ }}{E_{thap}}\)
Dựa vào sơ đồ mức năng lượng, ta có: \({E_3} - {\rm{ }}{E_1} = {\rm{ }}{E_3} - {\rm{ }}{E_2} + {\rm{ }}{E_2} - {\rm{ }}{E_1}\)
\({f_{31}} = {f_{32}} + {f_{21}} \to \dfrac{1}{{{\lambda _{31}}}} = \dfrac{1}{{{\lambda _{32}}}} + \dfrac{1}{{{\lambda _{21}}}}\)
\({f_{41}} = {f_{43}} + {f_{32}} + {f_{21}} \to \dfrac{1}{{{\lambda _{43}}}} + \dfrac{1}{{{\lambda _{32}}}} + \dfrac{1}{{{\lambda _{21}}}}\)
Số vạch quang phổ phát ra tối đa của một khối khí: \(\dfrac{{n(n - 1)}}{2}\)
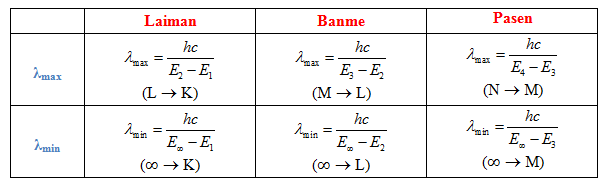
3. Dạng 3: tính \({\lambda _{{\bf{max}}}},{\lambda _{{\bf{min}}}}\) trong các dãy.
\(\dfrac{{hc}}{\lambda } = {\rm{ }}{E_n} - {\rm{ }}{E_m} \to \lambda = \dfrac{{hc}}{{{E_n} - {\rm{ }}{E_m}}}\); \({E_\infty } = {\rm{ }}0\)
Các bài khác cùng chuyên mục
- Phương pháp giải bài tập phân hạch - nhiệt hạch
- Phương pháp giải bài tập về phóng xạ
- Phương pháp giải bài tâp phản ứng hạt nhân
- Phương pháp giải bài tập của chuyển động electron quang điện trong điện trường đều và từ trường đều
- Phương pháp giải bài tập về cường độ dòng quang điện bão hòa và hiệu suất lượng tử
- Phương pháp giải bài tập phân hạch - nhiệt hạch
- Phương pháp giải bài tập về phóng xạ
- Phương pháp giải bài tâp phản ứng hạt nhân
- Phương pháp giải bài tập của chuyển động electron quang điện trong điện trường đều và từ trường đều
- Phương pháp giải bài tập về cường độ dòng quang điện bão hòa và hiệu suất lượng tử













Danh sách bình luận