Bài 8. Đường tròn

Bài 33 trang 115 Vở bài tập toán 6 tập 2

Giải bài 33 trang 115, 116 VBT toán 6 tập 2. Trên hình 27, ta có hai đường tròn (A; 3cm) và (B ; 2cm) cắt nhau tại C, D. AB = 4cm. Đường tròn tâm A, B lần lượt cắt đoạn thẳng AB tại K, I...

Đề bài

Trên hình 27, ta có hai đường tròn \((A;3cm)\) và \((B;2cm)\) cắt nhau tại \(C, D.\) \(AB = 4cm.\) Đường tròn tâm \(A,B\) lần lượt cắt đoạn thẳn \(AB\) tại \(K, I.\)

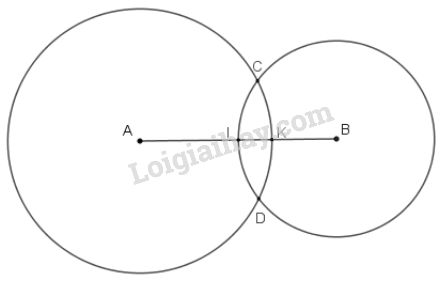
a) Tính \(CA, CB, DA,DB.\)

b) \(I\) có phải là trung điểm của đoạn thẳng \(AB\) không?

c) Tính \(IK.\)

Phương pháp giải - Xem chi tiết

Đường tròn tâm \(O,\) bán kính \(R\) là hình gồm các điểm cách \(O\) một khoảng bằng \(R,\) kí hiệu \((O;R).\)

Sử dụng công thức cộng đoạn thẳng: Nếu \(M\) nằm giữa hai điểm \(A,B\) thì \(AM+MB=AB\)

Sử dụng: Nếu \(M\) là trung điểm của đoạn thẳng \(AB\) thì \(MA=MB=\dfrac{AB}{2}\)

Lời giải chi tiết

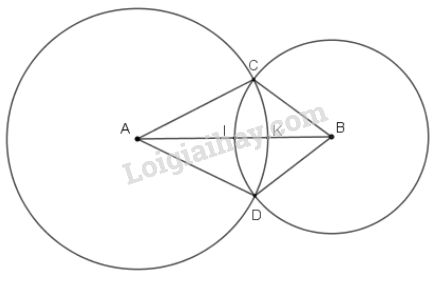
a) Vì hai đường tròn (A; 3cm) và (B; 2cm) cắt nhau tại C; D nên:

Hai điểm \(C\) và \(D\) nằm trên đường tròn \((A; 3cm)\) nên \(CA = DA = 3cm\)

Hai điểm \(C\) và \(D\) nằm trên đường tròn \((B; 2cm)\) nên \(CB = DB = 2cm\)

b) Đường tròn (B; 2cm) cắt đoạn AB tại I nên I nằm trên đường tròn (B; 2cm), suy ra BI = 2cm.

Trên tia \(BA\) có: \(BI = 2cm, AB = 4cm\)

Suy ra \(BI<BA\) \((2cm < 4cm)\) nên điểm \(I\) nằm giữa \(A\) và \(B\) (1).

Suy ra \(AI + IB = AB\)

\(\Rightarrow AI = AB - IB = 4 - 2 = 2cm\)

Do đó: \(AI = BI \,(=2cm)\) (2)

Từ (1) và (2) suy ra \(I\) là trung điểm của đoạn thẳng \(AB.\)

c) Đường tròn (A; 3cm) cắt đoạn AB tại K nên K thuộc đường tròn (A ; 3cm) , suy ra AK = 3cm.

Trên tia \(AB\) có \(AI = 2cm, AK = 3cm.\)

Vì \(AI < AK\) (\(2cm<3cm)\) nên điểm \(I\) nằm giữa hai điểm \(A\) và \(K.\)

Suy ra \(AI + IK = AK\)

\(\Rightarrow IK = AK - AI = 3 - 2 = 1cm\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.7 trên 10 phiếu

Bài tiếp theo

Bài 34 trang 116 Vở bài tập toán 6 tập 2
Giải bài 34 trang 116 VBT toán 6 tập 2. Với compa, hãy so sánh các đoạn thẳng trong hình 28 rồi đánh cùng một dấu cho các đoạn thẳng bằng nhau...
Bài 35 trang 117 Vở bài tập toán 6 tập 2
Giải bài 35 trang 117, 118 VBT toán 6 tập 2. Vẽ lại hình 29 (đúng kích thước như hình đã cho).
Bài 32 trang 114 Vở bài tập toán 6 tập 2
Giải bài 32 trang 114, 115 VBT toán 6 tập 2. Trên hình 26, ta có hai đường tròn (O ; 2cm) và (A; 2cm) cắt nhau tại C, D. Điểm A nằm trên đường tròn tâm O. a) Vẽ đường tròn tâm C, bán kính 2cm. b) Vì sao...
Bài 31 trang 114 Vở bài tập toán 6 tập 2
Giải bài 31 trang 114 VBT toán 6 tập 2. Vẽ đường tròn tâm O, bán kính 2cm. Vẽ đường kính AB và dây cung AC của đường tròn đó. Đường kính AB dài bao nhiêu ...
Phần câu hỏi bài 8 trang 114 Vở bài tập toán 6 tập 2
Giải phần câu hỏi bài 8 trang 114 VBT toán 6 tập 2. "Đường tròn" và "Hình tròn" khác nhau thế nào ?...