Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Ôn tập chương II - Tích vô hướng của hai vectơ và ứng d..
Bài 27 trang 66 SGK Hình học 10
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi R là bán kính đường tròn nội tiếp tam giác ABC.
Đề bài
Tam giác \(ABC\) vuông cân tại \(A\) và nội tiếp trong đường tròn tâm \(O\) bán kính \(R\). Gọi \(r\) là bán kính đường tròn nội tiếp tam giác \(ABC\). Khi đó tỉ số \({R \over r}\) là:
A. \(1 + \sqrt 2\)
B. \({{2 + \sqrt 2 } \over 2}\)
C. \({{\sqrt 2 - 1} \over 2}\)
D. \({{1 + \sqrt 2 } \over 2}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Tính bán kính R.
- Tính diện tích tam giác và nửa chu vi suy ra r.
- Tính tỉ số.
Lời giải chi tiết
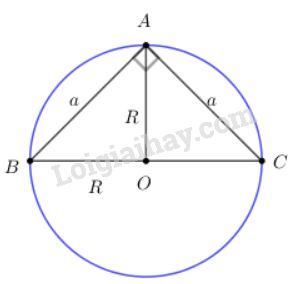
Đặt AB=AC=a.
+) Tam giác ABC vuông tại A nên theo Pitago ta có: \(BC =AB^2+AC^2\) \(= \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\(\Rightarrow R =\frac{1}{2}BC= \frac{{a\sqrt 2 }}{2}.\)
+) Nửa chu vi tam giác \(ABC\) là: \(p = \frac{{a + a + a\sqrt 2 }}{2}\) \(= \frac{{2a + a\sqrt 2 }}{2}\)
Ta có: \({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.a.a = \frac{{{a^2}}}{2}\)
Mà \({S_{ABC}} = pr\)
\(\Rightarrow r = \frac{{{S_{ABC}}}}{p} = \frac{{\frac{{{a^2}}}{2}}}{{\frac{{2a + a\sqrt 2 }}{2}}} \) \(= \frac{{{a^2}}}{2}:\frac{{2a + a\sqrt 2 }}{2} = \frac{{{a^2}}}{2}.\frac{2}{{2a + a\sqrt 2 }} = \frac{a}{{2 + \sqrt 2 }}\)
\(\Rightarrow \frac{R}{r}\) \( = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{a}{{2 + \sqrt 2 }}}}\)
\(= \frac{{a\sqrt 2 }}{2}:\frac{a}{{2 + \sqrt 2 }} = \frac{{a\sqrt 2 }}{2}.\frac{{2 + \sqrt 2 }}{a}\) \( = \frac{{\sqrt 2 \left( {2 + \sqrt 2 } \right)}}{2} = \sqrt 2 + 1\)
Vậy chọn A.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 28 trang 66 SGK Hình học 10
- Bài 29 trang 67 SGK Hình học 10
- Bài 30 trang 67 SGK Hình học 10
- Bài 26 trang 66 SGK Hình học 10
- Bài 25 trang 66 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
