Bài 91 trang 118 SBT Hình học 10 Nâng cao

Giải bài tập Bài 91 trang 118 SBT Hình học 10 Nâng cao

Đề bài

Cho parabol \((P): {y^2} = x\) và hai điểm \(A(1 ; -1), B(9 ; 3)\) nằm trên \((P)\). Gọi \(M\) là điểm thuộc cung \(AB\) của \((P)\) (phần của \((P)\) bị chắn bởi dây \(AB\)). Xác định vị trí của \(M\) trên cung \(AB\) sao cho tam giác \(MAB\) có diện tích lớn nhất.

Lời giải chi tiết

(h.123).

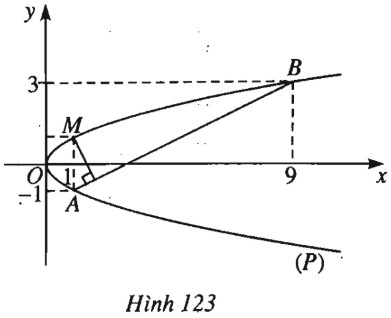
Phương trình đường thẳng \(AB: x-2y-3=0.\)

Vì \(M(x ; y)\) nằm trên cung \(AB\) của \((P)\) nên \( - 1 \le y \le 3\).Ta có: \(\begin{array}{l}{S_{MAB}} = \dfrac{1}{2}AB.d(M ; AB)\\ = \dfrac{1}{2}.\sqrt {{{(9 - 1)}^2} + {{(3 + 1)}^2}} . \dfrac{{|x - 2y - 3|}}{{\sqrt {{1^2} + {2^2}} }}\\ = 2.|x - 2y - 3| = 2|{y^2} - 2y - 3|\end{array}\)

Ta có \(f(y) = {y^2} - 2y - 3 \)

\(= {(y - 1)^2} - 4 \ge - 4\).

Suy ra \(f(y)\) nhỏ nhất bằng \(-4\) khi và chỉ khi \(y=1\). Mặt khác, \(f(-1)=f(3)=0\). Do đó trên đoạn \([-1 ; 3],\) hàm số \(|{y^2} - 2y - 3|\) lớn nhất bằng \(4\) khi và chỉ khi \(y=1\). Vậy \(S_MAB\) lớn nhất bằng \(8\) khi và chỉ khi \(M=(1 ; 1).\)

Loigiaihay.com