Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học Bài 6. Hàm số lũy thừa

Bài 61 sách giải tích 12 nâng cao trang 118


Vẽ đồ thị hàm số

Lựa chọn câu để xem lời giải nhanh hơn

Vẽ đồ thị hàm số y=log0,5x. Dựa vào đồ thị hãy giải các bất phương trình sau:

a) log0,5x > 0     b) -3 ≤ log0,5x < -1

LG a

Vẽ đồ thị hàm số \(y = {\log _{0,5}}x\) và giải bất phương trình \( {\log _{0,5}}x > 0\)

Lời giải chi tiết:

* Vẽ đồ thị hàm số \(y = {\log _{0,5}}x\)

TXĐ: \(D = \left( {0; + \infty } \right)\)

a = 0,5 < 1. Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).

Bảng giá trị: 

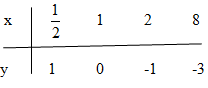
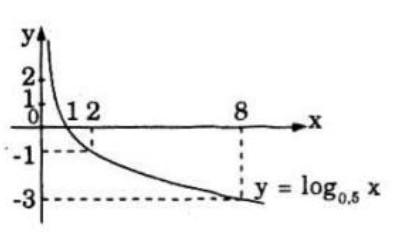
* Giải bất phương trình \( {\log _{0,5}}x > 0\)

Từ đồ thị ta thấy:

\({\log _{0,5}}x > 0 \Leftrightarrow 0 < x < 1\) (ứng với phần đồ thị ở phía trên trục hoành).

LG b

\( - 3 \le {\log _{0,5}}x \le  - 1\)

Lời giải chi tiết:

\( - 3 < {\log _{0,5}}x <  - 1 \Leftrightarrow 2 < x \le 8\) (ứng với những điểm trên đồ thị có tung độ thuộc nửa khoảng \(\left[ { - 3;1} \right)\)).

Loigiaihay.com


Bình chọn:
3.5 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi TN THPT & ĐH năm 2022 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua