Bài 57 sách giải tích 12 nâng cao trang 117

Trên hình bên cho hai đường cong (C1) (đường nét liền) và (C2) (đường nét đứt) được vẽ trên cùng một mặt phẳng tọa độ. Biết rằng mỗi đường cong ấy là đồ thị của ột trong hai hàm số lũy thừa và . Chỉ dựa vào tính chất của lũy thừa, có thể nhận biết đường cong nào là đồ thị của hàm số nào được không? Hãy nêu rõ lập luận.

Đề bài

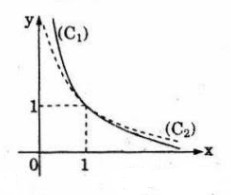
Trên hình bên cho hai đường cong ( ${C_1}$ ) (đường nét liền) và ( ${C_2}$ ) (đường nét đứt) được vẽ trên cùng một mặt phẳng tọa độ. Biết rằng mỗi đường cong ấy là đồ thị của một trong hai hàm số lũy thừa $y = {x^{ - 2}}$ và $y = {x^{ - {1 \over 2}}}\,\,\left( {x > 0} \right)$ . Chỉ dựa vào tính chất của lũy thừa, có thể nhận biết đường cong nào là đồ thị của hàm số nào được không? Hãy nêu rõ lập luận.

Phương pháp giải - Xem chi tiết

So sánh giá trị của 2 hàm số $y = {x^{ - 2}}$ và $y = {x^{ - {1 \over 2}}}\,\,\left( {x > 0} \right)$ tại x trên từng khoảng và đối chiếu đồ thị rồi kết luận.

Lời giải chi tiết

Với $x > 1$ ta có:

$- 2 < - \frac{1}{2} \Rightarrow {x^{ - 2}} < {x^{ - \frac{1}{2}}}$ (ví dụ ${2^{ - 2}} < {2^{ - \frac{1}{2}}}$ ) nên đồ thị hàm số $y = {x^{ - 2}}$ nằm dưới đồ thị hàm số $y = {x^{ - \frac{1}{2}}}$

Với $0 < x < 1$ ta có:

$- 2 < - \frac{1}{2} \Rightarrow {x^{ - 2}} > {x^{ - \frac{1}{2}}}$ nên đồ thị hàm số $y = {x^{ - 2}}$ nằm trên đồ thị hàm số $y = {x^{ - \frac{1}{2}}}$

Đối chiếu hai đường cong trong hình ta thấy,

+ Trong khoảng $\left( {1; + \infty } \right)$ thì $\left( {{C_1}} \right)$ nằm dưới $\left( {{C_2}} \right)$

+ Trong khoảng $\left( {0;1} \right)$ thì $\left( {{C_1}} \right)$ nằm trên $\left( {{C_2}} \right)$

Vậy $\left( {{C_1}} \right)$ là đồ thị hàm số $y = {x^{ - 2}}$

$\left( {{C_2}} \right)$ là đồ thị hàm số $y = {x^{ - \frac{1}{2}}}$

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 4 phiếu

Bài tiếp theo

Bài 58 sách giải tích 12 nâng cao trang 117
Tìm đạo hàm của các hàm số sau:
Bài 59 sách giải tích 12 nâng cao trang 117
Tính giá trị gần đúng đạo hàm của mỗi hàm số sau tại điểm đã cho (chính xác đến hàng phần trăm):
Bài 60 sách giải tích 12 nâng cao trang 117
a) Chứng minh rằng đồ thị của hai hàm số đối xứng với nhau qua trục tung. b) Chứng minh rằng đồ thị của hai hàm số đối xứng với nhau qua trục hoành.
Bài 61 sách giải tích 12 nâng cao trang 118
Vẽ đồ thị hàm số
Bài 62 sách giải tích 12 nâng cao trang 118
Vẽ đồ thị của hàm số . Dựa vào đồ thị, hãy giải thích các bất phương trình sau:

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.