 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Bài 7. Khảo sát sự biến thiên và vẽ đồ thị hàm số của m..
Bài 7. Khảo sát sự biến thiên và vẽ đồ thị hàm số của m..
Bài 55 trang 50 SGK giải tích 12 nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số b) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho biết rằng tiếp tuyến đó đi qua điểm (3;3).
LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = x - {2 \over {x - 1}}\)
Lời giải chi tiết:
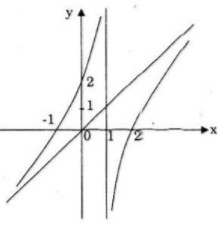
Tập xác định: \(D = R\backslash \left\{ 1 \right\}\)
\(y' = 1 + {2 \over {{{\left( {x - 1} \right)}^2}}} > 0,\forall x \in D\)
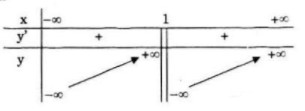
Vậy hàm số đồng biến trên khoảng \(( - \infty ;1)\) và \((1; + \infty )\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to {1^ - }} y = + \infty \cr
& \mathop {\lim }\limits_{x \to {1^ + }} y = - \infty \cr} \)
Do đó \(x=1\) là tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to \pm \infty } (y - x) = \mathop {\lim }\limits_{x \to \pm \infty } \left( { - {2 \over {x - 1}}} \right) = 0\)
Vậy \(y=x\) là tiệm cận xiên.
Bảng biến thiên:
Đồ thị giao \(Ox\) tại \((-1;0),(2;0)\)
Đồ thị giao \(Oy\) tại \((0;2)\)
LG b
Viết phương trình tiếp tuyến của đồ thị hàm số đã cho biết rằng tiếp tuyến đó đi qua điểm \((3;3)\).
Lời giải chi tiết:
Ta có: \(y' = 1 + {2 \over {{{\left( {x - 1} \right)}^2}}}\)
Phương trình tiếp tuyến với đồ thị hàm số đã cho tại điểm \(M\left( {{x_o};{{x_o} - {2 \over {{x_o} - 1}}}} \right) \in \left( C \right)\) là:
\(\left( d \right):\,y - {x_o} + {2 \over {{x_o} - 1}} \) \(= \left[ {1 + {2 \over {{{\left( {{x_o} - 1} \right)}^2}}}} \right]\left( {x - {x_o}} \right)\,\left( {x_o \ne 1} \right)\)
Vì \(\left( {3;3} \right) \in d\) nên \(3 - {x_o} + {2 \over {{x_o} - 1}} = {{{{\left( {{x_o} - 1} \right)}^2} + 2} \over {{{\left( {{x_o} - 1} \right)}^2}}}\left( {3 - {x_o}} \right)\)
\(\eqalign{
& \Leftrightarrow \left( {3 - {x_o}} \right){\left( {{x_o} - 1} \right)^2} + 2\left( {{x_o} - 1} \right) \cr&= \left( {{x_o^2} - 2{x_o} + 3} \right)\left( {3 - {x_o}} \right) \cr} \)
\(\begin{array}{l}
\Leftrightarrow \left( {3 - {x_o}} \right)\left( {x_o^2 - 2{x_o} + 1} \right) + 2{x_o} - 2\\
= 3x_o^2 - 6{x_o} + 9 - x_o^3 + 2x_o^2 - 3{x_o}\\
\Leftrightarrow 3x_o^2 - x_o^3 - 6{x_o} + 2x_o^2 + 3 - {x_o} + 2{x_o} - 2\\
= 3x_o^2 - 6{x_o} + 9 - x_o^3 + 2x_o^2 - 3{x_o}\\
\Leftrightarrow 4{x_o} - 8 = 0\\
\Leftrightarrow {x_o} = 2\\
\Rightarrow {y_o} = 2 - \frac{2}{{2 - 1}} = 0
\end{array}\)
\( \Rightarrow M\left( {2;0} \right)\)
Vậy phương trình tiếp tuyến cần tìm là: \(y = 3\left( {x - 2} \right)\) hay \(y = 3x - 6.\)
Cách khác:
Gọi phương trình đường thẳng (d) có hệ số góc k đi qua A(3; 3) có dạng
y-3=k(x-3) <=> y=k(x-3)+3
(d) là tiếp tuyến của đồ thị hàm số khi và chỉ khi hệ phương trình sau có nghiệm

Thế (2) vào (1) ta được:
\(\begin{array}{l}
\frac{{{x^2} - x - 2}}{{x - 1}} = \left( {1 + \frac{2}{{{{\left( {x - 1} \right)}^2}}}} \right)\left( {x - 3} \right) + 3\\
\Leftrightarrow \frac{{{x^2} - x - 2}}{{x - 1}} = \frac{{{{\left( {x - 1} \right)}^2} + 2}}{{{{\left( {x - 1} \right)}^2}}}\left( {x - 3} \right) + 3\\
\Leftrightarrow \frac{{{x^2} - x - 2}}{{x - 1}} = \frac{{\left( {{x^2} - 2x + 3} \right)\left( {x - 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} + 3\\
\Leftrightarrow \frac{{\left( {{x^2} - x - 2} \right)\left( {x - 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}\\
= \frac{{\left( {{x^2} - 2x + 3} \right)\left( {x - 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} + \frac{{3{{\left( {x - 1} \right)}^2}}}{{{{\left( {x - 1} \right)}^2}}}\\
\Rightarrow \left( {{x^2} - x - 2} \right)\left( {x - 1} \right)\\
= \left( {{x^2} - 2x + 3} \right)\left( {x - 3} \right) + 3\left( {{x^2} - 2x + 1} \right)\\
\Leftrightarrow {x^3} - {x^2} - 2x - {x^2} + x + 2\\
= {x^3} - 2{x^2} + 3x - 3{x^2} + 6x - 9 + 3{x^2} - 6x + 3\\
\Leftrightarrow - 4x + 8 = 0\\
\Leftrightarrow x = 2
\end{array}\)
* Với x = 2 thay vào (2) ta được k = 3.
Vậy phương trình tiếp tuyến là
y = 3(x- 3) + 3 hay y = 3x – 6
Loigiaihay.com












Danh sách bình luận