Bài 54 trang 50 SGK giải tích 12 nâng cao

a) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số b) Từ đồ thị (H) suy ra cách vẽ đồ thị của hàm số

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

LG a

Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số \(y = 1 - {1 \over {x + 1}}\)

Lời giải chi tiết:

\(y =f(x)= {x \over {x + 1}}\)
TXĐ: \(D = R\backslash \left\{ { - 1} \right\}\)
Tiệm cận đứng \(x = -1\) vì

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{x}{{x + 1}} = + \infty \\
\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{x}{{x + 1}} = - \infty
\end{array}\)

Tiệm cận ngang \(y = 1\) vì:

\(\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{x}{{x + 1}} = 1\)

\(y' = {1 \over {{{\left( {x + 1} \right)}^2}}} > 0\) với mọi \(x \ne - 1\) nên hàm số đồng biến trên các khoảng \(\left( { - \infty ;-1} \right)\) và \(\left( {-1; + \infty } \right)\)

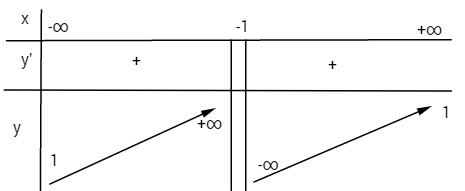
Điểm đặc biệt

\(\eqalign{
& x = 0 \Rightarrow y = 0 \cr
& x = 1 \Rightarrow y = {1 \over 2} \cr} \)

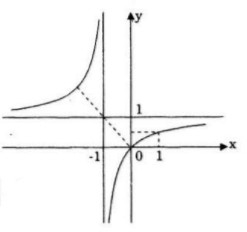
Đồ thị nhận \(I(-1;1)\) làm tâm đối xứng.

LG b

Từ đồ thị \((H)\) suy ra cách vẽ đồ thị của hàm số \(y = -1 + {1 \over {x + 1}}\)

Lời giải chi tiết:

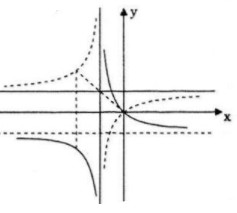
Ta có \(y = - 1 + {1 \over {x + 1}} = {{ - x} \over {x + 1}}=-f(x)\)

Do đó đồ thị của hàm số \(y = - 1 + {1 \over {x + 1}}\) là hình đối xứng của \((H)\) qua trục hoành.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.4 trên 5 phiếu

Bài tiếp theo

Bài 55 trang 50 SGK giải tích 12 nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số b) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho biết rằng tiếp tuyến đó đi qua điểm (3;3).
Bài 56 trang 50 SGK giải tích 12 nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số b) Từ đồ thị (C) suy ra cách vẽ đồ thị của hàm số
Bài 53 trang 50 SGK giải tích 12 nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số b) Viết phương trình tiếp tuyến của đồ thị hám số đã cho tại giao điểm A của đồ thị với trục tung. c) Viết phương trinh tiếp tuyến của đồ thị song song với tiếp tuyến tại điểm A.
Bài 52 trang 50 SGK giải tích 12 nâng cao
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
Bài 51 trang 49 SGK giải tích 12 nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: b) Chứng minh rằng giao điểm I của đường tiệm cận của đồ thị là tâm đối xứng của đồ thị. c) Tùy theo các giá trị của m, hãy biện luận số nghiệm của phương trình:
Bài 50 trang 49 SGK giải tích 12 nâng cao
Khảo sát sự biến thiên và vẽ đồ thị hàm số sau:
Bài 49 trang 49 SGK giải tích 12 nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số : b) Chứng minh rằng giao điểm I của hai đường tiệm cận của đồ thị là tâm đối xứng của đồ thị.