Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học Bài 7: Bất phương trình bậc hai

Bài 53 trang 145 SGK Đại số 10 nâng cao


Giải các bất phương trình:

Lựa chọn câu để xem lời giải nhanh hơn

Giải các bất phương trình

LG a

-5x2 + 4x + 12 < 0

Phương pháp giải:

Xét dấu vế trái, từ đó suy ra tập nghiệm của bpt.

Lời giải chi tiết:

Ta có:

\( - 5{x^2} + 4x + 12 = 0 \Leftrightarrow \left[ \matrix{
x = - {6 \over 5} \hfill \cr 
x = 2 \hfill \cr} \right.\)

Có a = -5 < 0 nên:

Bảng xét dấu:

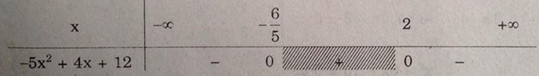Do đó, -5x2 + 4x + 12 < 0 khi

\(\left[ \begin{array}{l}
x < - \frac{6}{5}\\
x > 2
\end{array} \right.\)

Tập nghiệm của bất phương trình \(S = ( - \infty , - {6 \over 5}) \cup (2, + \infty )\)

LG b

16x2 + 40x +25 < 0

Lời giải chi tiết:

Ta có: \(16{x^2} + 40x + 25 = 0 \) \(\Leftrightarrow x =  - {5 \over 4}\) (nghiệm kép)

\(\eqalign{
& a = 16 > 0 \cr 
& \Delta ' = 200 - 16.25 = 0 \cr 
& \Rightarrow 16{x^2} + 40x + 25 \ge 0\,\,\forall x \in R \cr} \)

Nên không có giá trị nào của x để 16x2 + 40x +25 < 0.

Vậy S = Ø.

Cách khác:

\(16{x^2} + 40x + 25\) \( = {\left( {4x} \right)^2} + 2.\left( {4x} \right).5 + {5^2} \) \( = {\left( {4x + 5} \right)^2} \ge 0,\forall x\)

Nên không có giá trị nào của x để 16x2 + 40x +25 < 0.

Vậy S = Ø.

LG c

3x2 - 4x + 4 ≥ 0

Lời giải chi tiết:

Ta có:

a = 3

Δ’ = 4 – 12 = -8 < 0

⇒ 3x2 - 4x + 4 > 0 ∀x ∈ R

Nên với mọi x ta đều có 3x2 - 4x + 4 ≥ 0.

Vậy S = R

LG d

 x2 - x - 6 ≤ 0

Lời giải chi tiết:

Ta có:

\({x^2} - x - 6 = 0 \) \(\Leftrightarrow \left[ \matrix{
x = 3 \hfill \cr 
x = - 2 \hfill \cr} \right.\)

Có a = 1 > 0 nên bảng xét dấu:

Do đó, \({x^2} - x - 6 \le 0 \Leftrightarrow  - 2 \le x \le 3\) nên tập nghiệm S = [-2, 3]

Loigiaihay.com


Bình chọn:
4.5 trên 10 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store