 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Ôn tập chương IV - Số phức
Ôn tập chương IV - Số phức
Bài 42 trang 209 SGK giải tích 12 nâng cao
Bằng cách biển diễn hình học các số phức 2 + i, 5+ i và 8 + i, hãy chứng minh rằng
LG a
Bằng cách biểu diễn hình học các số phức 2 + i và 3 + i, hãy chứng minh rằng nếu \(\tan a = {1 \over 2},\,\tan b = {1 \over 3}\)với \(a,b \in \left( {0;{\pi \over 2}} \right)\) thì \(a + b = {\pi \over 4}\).
Phương pháp giải:
Tính acgumen của zz' bằng hai cách rồi suy ra đpcm.
Lời giải chi tiết:
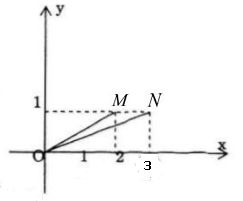
Biểu diễn hình học \(2 + i, 3 + i\) theo thứ tự bới M và N trong mặt phẳng phức
Ta có: \(\tan \left( {Ox,\,OM} \right) = {1 \over 2} = \tan a\)
\(\tan \left( {Ox,\,ON} \right) = {1 \over 3} = \tan b\)
Xét \(z.z' = (2 + i).(3 + i) = 5(1 + i) \)
\(= 5\sqrt 2 \left( {\cos {\pi \over 4} + i\sin {\pi \over 4}} \right)\)
Số \(zz'\) có acgumen là \({{\pi \over 4}}\).
Mà zz' cũng có acgumen là a+b.
Suy ra \(a + b = {\pi \over 4}\)
LG b
Bằng cách biển diễn hình học các số phức 2 + i, 5+ i và 8 + i, hãy chứng minh rằng nếu \(\tan a = {1 \over 2},\,\tan b = {1 \over 5},\,\tan c = {1 \over 8}\) với \(a,b,c \in \left( {0;{\pi \over 2}} \right)\) thì \(a + b + c = {\pi \over 4}\).
Lời giải chi tiết:
\({z_1} = 2 + i\) có một acgumen là a với \(\tan a = {1 \over 2}\)
\({z_2} = 5 + i\) có một acgumen là b với \(\tan b = {1 \over 5}\)
\({z_3} = 8 + i\) có một acgumen là c với \(\tan c = {1 \over 8}\)
Xét \(z = {z_1}{z_2}{z_3} = \left( {2 + i} \right)\left( {5 + i} \right)\left( {8 + i} \right) \) \(= 65\left( {1 + i} \right)\)
\(= 65\sqrt 2 \left( {{{\sqrt 2 } \over 2} + i{{\sqrt 2 } \over 2}} \right) \) \(= 65\sqrt 2 \left( {\cos {\pi \over 4} + i\sin {\pi \over 4}} \right)\)
\(z\) có acgumen là \({\pi \over 4}\), suy ra \(a + b + c = {\pi \over 4}\)
Loigiaihay.com












Danh sách bình luận