 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Ôn tập chương IV - Số phức
Ôn tập chương IV - Số phức
Bài 38 trang 209 SGK giải tích 12 nâng cao
Chứng minh rằng
Đề bài
Chứng minh rằng \(\left| z \right| = \left| {\rm{w}} \right| = 1\) thì số \({{z + {\rm{w}}} \over {1 + z{\rm{w}}}}\) là số thực (giả sử \(1 + z{\rm{w}} \ne 0\)).
Phương pháp giải - Xem chi tiết
Sử dụng tính chất:
Số phức z=a+bi là số thực nếu \(\overline z = z\)
Lời giải chi tiết
Ta có \(z.\overline z = {\left| z \right|^2} = 1 \Rightarrow \overline z = {1 \over z}\). Tương tự \(\overline {\rm{w}} = {1 \over {\rm{w}}}\)
Do đó \(\overline {\left( {{{z + {\rm{w}}} \over {1 + z{\rm{w}}}}} \right)} = {{\overline z + \overline {\rm{w}} } \over {1 + \overline z .\overline {\rm{w}} }} = {{{1 \over z} + {1 \over {\rm{w}}}} \over {1 + {1 \over z}.{1 \over {\rm{w}}}}} = {{z + {\rm{w}}} \over {1 + z{\rm{w}}}}\).
Suy ra \({{z + {\rm{w}}} \over {1 + z{\rm{w}}}}\) là số thực.
Cách khác:
Giả sử z=a+bi,w=a'+b'i với a2+b2=a'2+b'2=1 và 1+zw ≠ 0
Vì |z| = 1 nên z.z−=1
Khi đó, ta có:
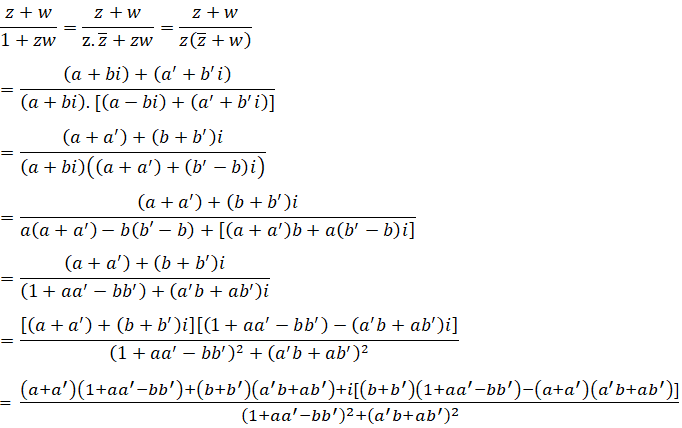
Xét phần ảo ở trên tử số ta có: (b+b' )(1+aa'-bb' )-(a+a' )(a' b+ab' )
=b+baa'-b2b'+b'+b' aa'-bb'2-aa' b-a2 b'-a'2 b-a'ab'
=b+b'-b' (a2+b2 )-b(b'2+a'2 )=b+b'-b'-b=0
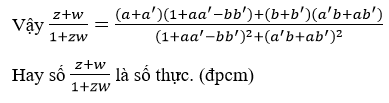
Loigiaihay.com












Danh sách bình luận