 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 Bài 4: Dấu của nhị thức bậc nhất
Bài 4: Dấu của nhị thức bậc nhất
Bài 40 trang 127 SGK Đại số 10 nâng cao
Giải bất phương trình và bất phương trình
Giải bất phương trình và bất phương trình
LG a
|x + 1| + |x – 1| = 4 (1)
Phương pháp giải:
Xét dấu các biểu thức dưới dấu giá trị tuyệt đối, từ đó phá dấu giá trị tuyệt đối giải phương trình thu được.
Lời giải chi tiết:
Ta có bảng:

ii) Với \(-1 ≤ x ≤ 1\), ta có: (1) \(⇔ x + 1 – x + 1 = 4 ⇔ 2 = 4\) (vô nghiệm)
iii) Với \(x > 1\), ta có (1) \(⇔ x + 1 + x – 1 = 4 \) \(\Leftrightarrow 2x = 4 \Leftrightarrow x = 2\) (nhận)
Vậy S = {-2, 2}
LG b
\({{|2x - 1|} \over {(x + 1)(x - 2)}} > {1 \over 2}\)
Phương pháp giải:
Phá dấu giá trị tuyệt đối, giải bất phương trình bằng cách lập bảng xét dấu.
Lời giải chi tiết:
Ta có:
i) Nếu \(x \le {1 \over 2}\) thì bất phương trình trở thành:
\(\eqalign{
& {{ - 2x + 1} \over {(x + 1)(x - 2)}} > {1 \over 2}\cr& \Leftrightarrow {{2( - 2x + 1) - (x + 1)(x - 2)} \over {2(x + 1)(x - 2)}} > 0 \cr
& \Leftrightarrow {{ - {x^2} - 3x + 4} \over {2(x + 1)(x - 2)}} > 0\cr & \Leftrightarrow {{(x - 1)(x + 4)} \over {2(x + 1)(x - 2)}} < 0 \cr} \)
Lập bảng xét dấu:
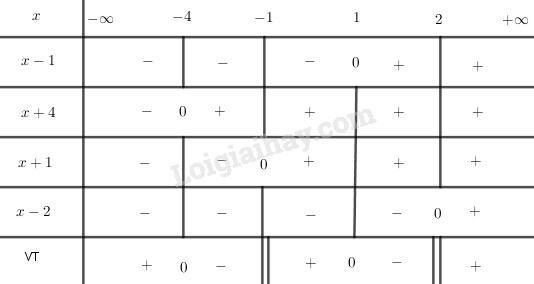
Từ bảng xét dấu ta thấy
\(\left[ \begin{array}{l}
- 4 < x < - 1\\
1 < x < 2
\end{array} \right.\)
Kết hợp \(x \le {1 \over 2}\) ta có: \(-4 < x < -1\).
ii) Nếu \(x > {1 \over 2}\) thì bất phương trình đã cho trở thành: \({{2x - 1} \over {(x + 1)(x - 2)}} > {1 \over 2}\)
Ta có:
\(\eqalign{
& {{2x - 1} \over {(x + 1)(x - 2)}} > {1 \over 2} \cr&\Leftrightarrow {{2(2x - 1) - (x + 1)(x - 2)} \over {2(x + 1)(x - 2)}} > 0 \cr
& \Leftrightarrow {{x(x - 5)} \over {2(x + 1)(x - 2)}} < 0 \cr} \)
Lập bảng xét dấu trên nửa khoảng \(({1 \over 2}, + \infty )\)
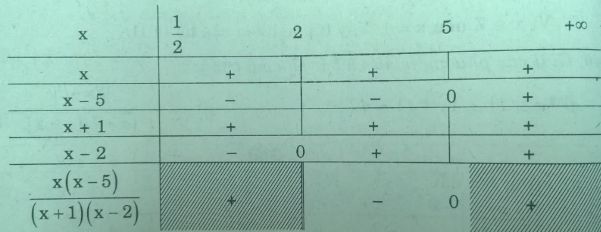
Trong trường hợp này ta có: \(2 < x < 5\)
Vậy \(S = (-4, -1) ∪ (2, 5)\)
Loigiaihay.com












Danh sách bình luận