 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 Bài 4: Dấu của nhị thức bậc nhất
Bài 4: Dấu của nhị thức bậc nhất
Bài 35 trang 126 SGK Đại số 10 nâng cao
Giải các hệ bất phương trình
Giải các hệ bất phương trình
LG a
\(\left\{ \matrix{
(x - 3)(\sqrt 2 - x) > 0 \hfill \cr
{{4x - 3} \over 2} < x + 3 \hfill \cr} \right.\)
Phương pháp giải:
Giải từng bất phương trình có trong hệ, kết hợp nghiệm và kết luận.
Lời giải chi tiết:
Ta có bảng xét dấu:
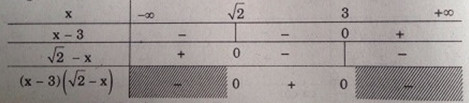
Ta có:
\(\eqalign{
& (x - 3)(\sqrt 2 - x) > 0 \cr &\Leftrightarrow \sqrt 2 < x < 3\,\,(1) \cr
& {{4x - 3} \over 2} < x + 3 \cr &\Leftrightarrow 2x < 9 \Leftrightarrow x < {9 \over 2}\,\,\,(2) \cr} \)
Từ (1) và (2) ta có: \(\sqrt 2 < x < 3\)
Vậy \(S = (\sqrt 2 ,3)\)
LG b
\(\left\{ \matrix{
{2 \over {2x - 1}} \le {1 \over {3 - x}} \hfill \cr
|x| < 1 \hfill \cr} \right.\)
Lời giải chi tiết:
Ta có:
\(\eqalign{
& {2 \over {2x - 1}} \le {1 \over {3 - x}} \cr &\Leftrightarrow {2 \over {2x - 1}} - {1 \over {3 - x}} \le 0 \cr
& \Leftrightarrow {{6 - 2x - 2x + 1} \over {(2x - 1)(3 - x)}} \le 0 \cr &\Leftrightarrow {{ - 4x + 7} \over {(2x - 1)(3 - x)}} \le 0 \cr} \)
Bảng xét dấu:
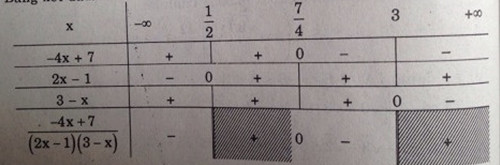
Ta có:
\({{ - 4x + 7} \over {(2x - 1)(3 - x)}} \le 0 \Leftrightarrow \left[ \matrix{
x < {1 \over 2} \hfill \cr
{7 \over 4} \le x < 3 \hfill \cr} \right.\)
Hệ đã cho tương đương với:
\(\left\{ \matrix{
\left[ \matrix{
x < {1 \over 2} \hfill \cr
{7 \over 4} \le x < 3 \hfill \cr} \right. \hfill \cr
- 1 < x < 1 \hfill \cr} \right. \Leftrightarrow - 1 < x < {1 \over 2}\)
Vậy \(S = ( - 1;{1 \over 2})\)
Loigiaihay.com












Danh sách bình luận