Bài 33 trang 126 SGK Đại số 10 nâng cao

Phân tích các đa thức sau thành nhân tử bậc nhất rồi xét dấu:

Lựa chọn câu để xem lời giải nhanh hơn

LG a.
LG b.

Phân tích các đa thức sau thành nhân tử bậc nhất rồi xét dấu:

LG a.

\(–x^2+ x + 6\)

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}
- {x^2} + x + 6\\
= - {x^2} + 3x - 2x + 6\\
= - x\left( {x - 3} \right) - 2\left( {x - 3} \right)\\
= \left( {x - 3} \right)\left( { - x - 2} \right)
\end{array}\)

Và \(x - 3 = 0 \Leftrightarrow x = 3; \) \(- x - 2 = 0 \Leftrightarrow x = - 2\)

Ta có bảng xét dấu:

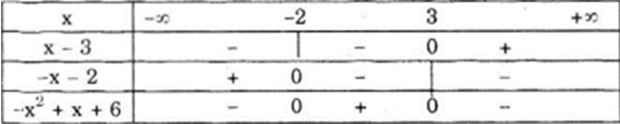
Chú ý:

Có thể dùng chú ý dưới đây để phân tích đa thức thành nhân tử:

Nếu đa thức \(f\left( x \right) = a{x^2} + bx + c\) có nghiệm \(x=x_1\) và \(x=x_2\) thì f(x) có thể được viết lại là:

\(f\left( x \right) = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\)

Cụ thể:

Ta thấy \(f\left( x \right) = - {x^2} + x + 6\) có \(a=-1\) và hai nghiệm \(x_1=-2,x_2=3\) nên \(f\left( x \right) = - \left( {x + 2} \right)\left( {x - 3} \right) \) \(= \left( { - x - 2} \right)\left( {x - 3} \right)\)

LG b.

\(2{x^2} - (2 + \sqrt 3 )x + \sqrt 3 \)

Phương pháp giải:

Có thể dùng chú ý dưới đây để phân tích đa thức thành nhân tử:

Nếu đa thức \(f\left( x \right) = a{x^2} + bx + c\) có nghiệm \(x=x_1\) và \(x=x_2\) thì f(x) có thể được viết lại là:

\(f\left( x \right) = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\)

Lời giải chi tiết:

Phương trình \(2{x^2} - (2 + \sqrt 3 )x + \sqrt 3 =0\) có hai nghiệm là x₁ = 1 và \({x_2} = {{\sqrt 3 } \over 2}\)

Do đó:

\(2{x^2} - (2 + \sqrt 3 )x + \sqrt 3 \) \(= 2(x - 1)(x - {{\sqrt 3 } \over 2}) \)

\(= (x - 1)(2x - \sqrt 3 )\)

Ta có bảng xét dấu sau:

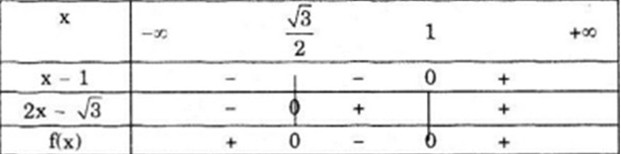
Chú ý:

Có thể phân tích đa thức đã cho thành nhân tử như sau:

\(\begin{array}{l}
2{x^2} - \left( {2 + \sqrt 3 } \right)x + \sqrt 3 \\
= 2{x^2} - 2x - \sqrt 3 x + \sqrt 3 \\
= 2x\left( {x - 1} \right) - \sqrt 3 \left( {x - 1} \right)\\
= \left( {x - 1} \right)\left( {2x - \sqrt 3 } \right)
\end{array}\)

Loigiaihay.com