Bài 16 trang 28 SKG Hình học 12 Nâng cao

Hãy chia một khối tứ diện thành hai khối tứ diện sao cho tỉ số thể tích của hai khối tứ diện này bằng một số k > 0 cho trước.

Đề bài

Hãy chia một khối tứ diện thành hai khối tứ diện sao cho tỉ số thể tích của hai khối tứ diện này bằng một số \(k>0\) cho trước.

Lời giải chi tiết

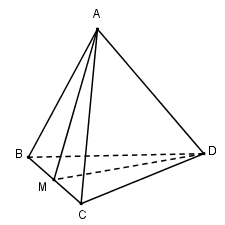
Cho khối tứ diện \(ABCD\).

Trên cạnh \(BC\) lấy một điểm \(M\).

Ta thấy \(d\left( {A,\left( {BMD} \right)} \right) = d\left( {A,\left( {CMD} \right)} \right)\)

Khi đó,

\(\begin{array}{l}
\frac{{{V_{A.BMD}}}}{{{V_{A.CMD}}}} = \frac{{\frac{1}{3}{S_{BMD}}.d\left( {A,\left( {BMD} \right)} \right)}}{{\frac{1}{3}{S_{CMD}}.d\left( {A,\left( {CMD} \right)} \right)}}\\
= \frac{{{S_{BMD}}}}{{{S_{CMD}}}} = \frac{{BM}}{{CM}}
\end{array}\)

Do đó \(\frac{{{V_{A.BMD}}}}{{{V_{A.CMD}}}} = k \Leftrightarrow \frac{{BM}}{{CM}} = k\)

Vậy lấy điểm M sao cho BM=kCM ta được mặt phẳng \((AMD)\) chia khối tứ diện \(ABCD\) thành hai khối tứ diện có tỉ số thể tích bằng \(k\).

Chú ý:

Ngoài cạnh BC thì có thể chọn các cạnh khác của tứ diện để lấy điểm M, chẳng hạn CM=kMD hay AM=kMD ta đều chia được thỏa mãn bài toán.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 4 phiếu

Bài tiếp theo

Bài 17 trang 28 Hình học 12 Nâng cao
Tính thể tích của khối hộp ABCD.A'B'C'D', biết rằng AA'B'D' là khối tứ diện đều cạnh a.
Bài 18 trang 28 SGK Hình học 12 Nâng cao
Tính thể tích của khối lăng trụ n-giác đều có tất cả các cạnh đều bằng a.
Bài 19 trang 28 SGK Hình học 12 Nâng cao
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông tại A, AC = b. . Đường thẳng BC’ tạo với mp(AA’C’C) một góc . a) Tính độ dài đoạn thẳng AC. b) Tính thể tích khối lăng trụ đã cho.
Bài 20 trang 28 SGK Hình học 12 Nâng cao
Cho khối lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh a, điểm A' cách đều ba điểm A, B, c, cạnh bên AA' tạo với mặt phẳng đáy một góc 60°. a) Tính thể tích của khối lăng trụ đó. b) Chứng minh rằng mặt bên BCCB' là một hình chữ nhật. c) Tính tổng diện tích các mặt bên của hình lăng trụ ABC.A'B'C (tổng đó gọi là diện tích xung quanh của hình (hoặc khối) lăng trụ đã cho).
Bài 21 trang 28 SGK Hình học 12 Nâng cao
Cho điểm M nằm trong hình tứ diện đều ABCD. Chứng minh rằng tổng các khoảng cách từ M tới bốn mặt của hình tứ diện là một số không phụ thuộc vào vị trí của điểm M. Tổng đó bằng bao nhiêu nếu cạnh của tứ diện đều bằng a ?
Bài 22 trang 28 SGK Hình học 12 Nâng cao
Cho khối lăng trụ tam giác đều ABC.A'B’C. Gọi M là trung điểm của AA’. Mặt phẳng đi qua M, B’, C chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó.
Bài 23 trang 29 SGK Hình học 12 Nâng cao
Cho khối chóp tam giác S.ABC. Trên ba đường thẳng SA, SB,SC lần lượt lấy ba điểm A’, B’, C' khác với S. Gọi V và V’ lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C'. Chứng minh rằng:
Bài 24 trang 29 SKG Hình học 12 Nâng cao
Khối chóp S.ABCD có đáy là hình bình hành, M là trung điểm của cạnh SC. Mặt phẳng (P) đi qua AM, song song với BD chia khối chóp thành hai phần. Tính tỉ số thể tích cùa hai phần đó.
Bài 25 trang 29 SGK Hình học 12 Nâng cao
Chứng minh rằng nếu có phép vị tự tỉ số k biến tứ diện ABCD thành tứ diện A’B’C’D’ thì
Bài 15 trang 28 Hình học 12 Nâng cao
Cho tam giác ABC cố định và một điểm S thay đổi. Thể tích của khối chóp S.ABC có thay đổi hay không nếu: a) Đỉnh S di chuyển trên một mặt phẳng song song với mặt phẳng (ABC) ; b) Đỉnh S di chuyển trên một mặt phẳng song song với chỉ một cạnh đáy ; c) Đỉnh S di chuyển trên một đường thẳng song song với một cạnh đáy ?