Giải SBT toán hình học và đại số 10 nâng cao Bài tập Ôn tập chương III - Phương pháp tọa độ trong mặ..

Bài 109 trang 123 SBT Hình học 10 Nâng cao


Giải bài tập Bài 109 trang 123 SBT Hình học 10 Nâng cao

Lựa chọn câu để xem lời giải nhanh hơn

Cho parabol \((P):\,{y^2} = 2px\,\,(p > 0)\).

 

LG a

Tìm độ dài của dây cung vuông góc với trục đối xứng của \((P)\) tại tiêu điểm \(F\) của \((P)\).

 

Lời giải chi tiết:

(h.134).

 

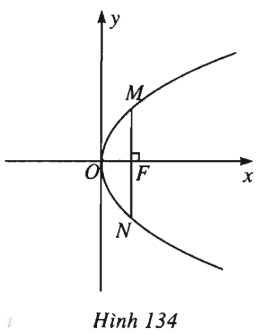
Gọi \(M , N\) là các giao điểm của \((P)\) và đường thẳng vuông góc với \(Ox\) tại \(F\). Khi đó, toạ độ của \(M, N\) là nghiệm của hệ \(\left\{ \begin{array}{l}x =  \dfrac{p}{2}\\{y^2} = 2px\end{array} \right.\)

Hệ có hai nghiệm là \(\left( { \dfrac{p}{2} ; p} \right) , \left( { \dfrac{p}{2} ;  - p} \right)\).

Vậy \(MN = |{y_M}| + |{y_N}| = 2p\).

 

LG b

\(A\) là một điểm cố định trên \((P)\). Một góc vuông \(uAt\) quay quanh đỉnh \(A\) có các cạnh cắt \((P)\) tại \(B\) và \(C\). Chứng minh rằng đường thẳng \(BC\) luôn đi qua một điểm cố định.

 

Lời giải chi tiết:

(h.135).

 

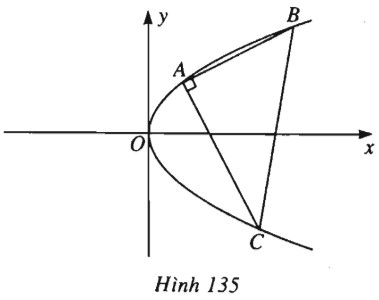
Giả sử \(A = \left( { \dfrac{{{a^2}}}{{2p}} ; a} \right) ,\) \(  B = \left( { \dfrac{{{b^2}}}{{2p}} ; b} \right) , \) \( C = \left( { \dfrac{{{c^2}}}{{2p}} ; c} \right)\).

Phương trình đường thẳng \(BC\) là:

\(\begin{array}{l}2px - (b + c)y + bc = 0.             (1)\\\overrightarrow {AB}  = \left( { \dfrac{{{b^2} - {a^2}}}{{2p}} ; b - a} \right) ,\\\overrightarrow {AC}  = \left( { \dfrac{{{c^2} - {a^2}}}{{2p}} ; c - a} \right).\\\overrightarrow {AB}  \bot \overrightarrow {AC}    \Leftrightarrow   \overrightarrow {AC} .\overrightarrow {AC}  = 0 \\   \Leftrightarrow   ({b^2} - {a^2})({c^2} - {a^2})\\ + 4{p^2}(b - a)(c - a) = 0\\ \Leftrightarrow   (b + a)(c + a) + 4{p^2} = 0\\ \Leftrightarrow   bc + a(b + c) + {a^2} + 4{p^2} = 0.       (2)\end{array}\)

Rút \(bc\) từ (2) thay vào (1), ta được phương trình của \(BC\) là

\(2px - {a^2} - 4{p^2} - (b + c)(y + a) = 0\)                 (3)

Dễ thấy đường thẳng \(BC\) có dạng (3) luôn đi qua điểm cố định \(M = \left( { \dfrac{{{a^2}}}{{2p}} + 2p ;  - a} \right)\).

Loigiaihay.com

 

Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

2k8 Tham gia ngay group chia sẻ, trao đổi tài liệu học tập miễn phí

>> Học trực tuyến Lớp 10 tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua