Trắc nghiệm Bài 20. Bài tập mạch dao động LC - Các đại lượng đặc trưng - Vật Lí 12
Đề bài
Mạch dao động điện từ điều hoà có cấu tạo gồm
-
A.
Nguồn điện một chiều và tụ điện mắc thành mạch kín.
-
B.
Nguồn điện một chiều và cuộn cảm mắc thành mạch kín.
-
C.
Nguồn điện một chiều và điện trở mắc thành mạch kín.
-
D.
Tụ điện và cuộn cảm mắc thành mạch kín.
Dao động điện từ tự do trong mạch dao động LC được hình thành là do hiện tượng nào sau đây?
-
A.
Hiện tượng cảm ứng điện từ.
-
B.
Hiện tượng cộng hưởng điện.
-
C.
Hiện tượng tự cảm.
-
D.
Hiện tượng từ hóa.
Mạch dao động điện từ gồm tụ điện C và cuộn cảm L, dao động tự do với tần số góc
-
A.
\(\omega = 2\pi \sqrt {LC} \)
-
B.
\(\omega = \frac{{2\pi }}{{\sqrt {LC} }}\)
-
C.
\(\omega = \sqrt {LC} \)
-
D.
\(\omega = \frac{1}{{\sqrt {LC} }}\)
Mạch dao động điện từ điều hoà LC có chu kỳ
-
A.
Phụ thuộc vào L, không phụ thuộc vào C.
-
B.
Phụ thuộc vào C, không phụ thuộc vào L.
-
C.
Phụ thuộc vào cả L và C.
-
D.
Không phụ thuộc vào L và C.
Mạch dao động điện từ điều hoà gồm cuộn cảm L và tụ điện C, khi tăng điện dung của tụ điện lên 4 lần thì chu kỳ dao động của mạch
-
A.
Tăng lên 4 lần.
-
B.
Tăng lên 2 lần.
-
C.
Giảm đi 4 lần.
-
D.
Giảm đi 2 lần.
Mạch dao động điện từ điều hoà gồm cuộn cảm L và tụ điện C. Khi tăng độ tự cảm của cuộn cảm lên 2 lần và giảm điện dung của tụ điện đi 2 lần thì tần số dao động của mạch
-
A.
Không đổi.
-
B.
Tăng 2 lần.
-
C.
Giảm 2 lần.
-
D.
Tăng 4 lần.
Cường độ dòng điện tức thời trong mạch dao động LC có dạng i = 0,05sin2000t(A). Tần số góc dao động của mạch là
-
A.
318,5 rad/s.
-
B.
318,5 H.
-
C.
2000 rad/s.
-
D.
2000 Hz.
Mạch dao động LC gồm cuộn cảm có độ tự cảm L = 2mH và tụ điện có điện dung C = 2pF, (lấy π2 = 10). Tần số dao động của mạch là:
-
A.
f = 2,5Hz.
-
B.
f = 2,5MHz
-
C.
f = 1Hz.
-
D.
f = 1MHz.
Mạch dao động điện từ gồm tụ điện C = 16nF và cuộn cảm L = 25mH. Tần số góc dao động của mạch là:
-
A.
ω = 200Hz.
-
B.
ω = 200rad/s.
-
C.
ω = 5.10-5
-
D.
ω = 5.104rad/s.
Cường độ dòng điện tức thời trong mạch dao động LC có dạng $i= 0,02cos2000t(A)$. Tụ điện trong mạch có điện dung $5μF$. Độ tự cảm của cuộn cảm là:
-
A.
L = 50mH
-
B.
L = 50H
-
C.
L = 5.10-6H
-
D.
L = 5.10-8H
Mạch dao động LC có điện tích trong mạch biến thiên điều hoà theo phương trình \(q = 4cos(2π.10^4t)μC\) . Tần số dao động của mạch là:
-
A.
f = 10(Hz).
-
B.
f = 10(kHz).
-
C.
f = 2π(Hz).
-
D.
f = 2π(kHz).
Trong mạch dao động điện từ tự do LC, so với dòng điện trong mạch thì điện áp giữa hai bản tụ điện luôn:
-
A.
Cùng pha.
-
B.
Trễ pha hơn một góc π/2.
-
C.
Sớm pha hơn một góc π/4.
-
D.
Sớm pha hơn một góc π/2.
Mạch dao động điện từ dao động tự do với tần số góc ω. Biết điện tích cực đại trên tụ điện là q0. Cường độ dòng điện đi qua cuộn dây thuần cảm có giá trị cực đại là:
-
A.
I0 = ω q0.
-
B.
I0 = ω2 q0
-
C.
I0 = 2ω q0.
-
D.
I0 = ω.q02.
Gọi U0 là điện áp cực đại giữa hai đầu bản tụ điện, I0 là cường độ dòng điện cực đại đi qua cuộn cảm. Biểu thức liên hệ giữa U0 và I0 của mạch dao động LC là:
-
A.
\({I_0} = {\text{ }}{U_0}\sqrt {\dfrac{C}{L}} \)
-
B.
\({U_0} = {\text{ }}{I_0}\sqrt {\dfrac{C}{L}} \)
-
C.
\({U_0} = {\text{ }}{I_0}\sqrt {LC} \)
-
D.
\({I_0} = {\text{ }}{U_0}\sqrt {LC} \)
Một mạch dao động gồm cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C. Nếu gọi I0 là cường độ dòng điện cực đại trong mạch, thì hệ thức liên hệ điện tích cực đại trên bản tụ điện q0 và I0 là:
-
A.
\({q_0} = \sqrt {\frac{{CL}}{\pi }} {I_0}\)
-
B.
\({q_0} = {I_0}\sqrt {LC}\)
-
C.
\({q_0} = \sqrt {\frac{C}{{\pi L}}} {I_0}\)
-
D.
\({q_0} = \sqrt {\frac{1}{{CL}}} {I_0}\)
Mạch dao động điện từ điều hoà LC gồm tụ điện C = 30nF và cuộn cảm L =25mH. Nạp điện cho tụ điện đến hiệu điện thế 4,8V rồi cho tụ phóng điện qua cuộn cảm, cường độ dòng điện hiệu dụng trong mạch là:
-
A.
I = 3,72mA.
-
B.
I = 4,28mA.
-
C.
I = 5,20mA.
-
D.
I = 6,34mA.
Một mạch dao động gồm một tụ điện có điện dung C = 18 nF và một cuộn dây thuần cảm có độ tự cảm L = 6 μH. Điện áp cực đại ở hai đầu tụ điện là 4V, cường độ dòng điện cực đại trong mạch là:
-
A.
87,2 mA.
-
B.
219 mA.
-
C.
12 mA.
-
D.
21,9 mA
Nhận xét nào sau đây về đặc điểm của mạch dao động điện từ điều hoà LC là không đúng?
-
A.
Điện tích trong mạch biến thiên điều hoà.
-
B.
Năng lượng điện trường tập trung chủ yếu ở tụ điện.
-
C.
Năng lượng từ trường tập trung chủ yếu ở cuộn cảm.
-
D.
Tần số dao động của mạch phụ thuộc vào điện tích của tụ điện.
Khi mắc tụ điện có điện dung C1 với cuộn cảm L thì tần số dao động của mạch là f1, khi mắc tụ điện có điện dung C2 với cuộn cảm L thì tần số dao động của mạch là f2. Khi mắc song song C1 với C2 và mắc với cuộn cảm L thì tần số dao động của mạch là:
-
A.
$\dfrac{1}{{f_{//}^2}} = \dfrac{1}{{f_1^2}} + \dfrac{1}{{f_2^2}}$
-
B.
$f_{//}^2 = f_1^2 + f_2^2{\text{ }}$
-
C.
$\dfrac{1}{{f_{//}^2}} = \dfrac{1}{{f_1^2}} - \dfrac{1}{{f_2^2}}$
-
D.
$f_{//}^2 = f_1^2 - f_2^2$
Khi mắc tụ điện có điện dung C1 với cuộn cảm L thì tần số dao động của mạch là f1, khi mắc tụ điện có điện dung C2 với cuộn cảm L thì tần số dao động của mạch là f2. Khi mắc C1 nối tiếp với C2 và mắc với cuộn cảm L thì tần số dao động của mạch là:
-
A.
$\frac{1}{{f_{nt}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}}$
-
B.
$f_{nt}^2 = f_1^2 + f_2^2{\text{ }}$
-
C.
$\frac{1}{{f_{nt}^2}} = \frac{1}{{f_1^2}} - \frac{1}{{f_2^2}}$
-
D.
$f_{nt}^2 = f_1^2 - f_2^2$
Khi mắc tụ điện có điện dung C1 với cuộn cảm có độ tự cảm L thì tần số dao động của mạch là f1 = 6kHz; khi mắc tụ điện có điện dung C2 với cuộn cảm có độ tự cảm L thì tần số dao động của mạch là f2 = 8kHz. Khi mắc C1 song song C2 với cuộn cảm có độ tự cảm L thì tần số dao động của mạch là bao nhiêu?
-
A.
f = 4,8kHz.
-
B.
f = 7kHz.
-
C.
f = 10kHz.
-
D.
f = 14kHz.
Khi mắc tụ điện có điện dung C1 với cuộn cảm L thì chu kì dao động của mạch là T1 = 2 ms; khi mắc tụ điện có điện dung C2 với cuộn L thì chu kì dao động của mạch là T2 = 1,5 ms. Khi mắc nối tiếp C1 và C2 với cuộn L thì chu kì dao động của mạch là bao nhiêu?
-
A.
T = 0,694 ms
-
B.
T= 0,857 ms.
-
C.
T = 1,2 ms.
-
D.
T = 1,44 ms.
Khi mắc cuộn cảm có độ tự cảm L1 với tụ điện có điện dung C thì tần số dao động của mạch là f1, khi mắc cuộn cảm có độ tự cảm L2 với tụ điện có điện dung C thì tần số dao động của mạch là f2. Nhận định nào sau đây là đúng:
-
A.
Khi mắc L1 nối tiếp L2: $f_{nt}^2 = f_1^2 + f_2^2{\text{ }}$
-
B.
Khi mắc L1 song song L2: $T_{//}^2 = T_1^2 + T_2^2{\text{ }}$
-
C.
Khi mắc L1 nối tiếp L2: $T_{nt}^2 = T_1^2 + T_2^2$
-
D.
Khi mắc L1 song song L2: $\frac{1}{{f_{//}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}}$
Khi mắc cuộn cảm có độ tự cảm L1 với tụ điện có điện dung C thì tần số dao động của mạch là f1 = 3 kHz, khi mắc cuộn cảm có độ tự cảm L2 với tụ điện có điện dung C thì tần số dao động của mạch là f2= 4 kHz. Tần số dao động của mạch khi mắc L1 nối tiếp với L2 và tần số dao động của mạch khi mắc L1 song song L2 là:
-
A.
fnt = 2,4 kHz và f// = 5 kHz
-
B.
fnt = 5,76 kHz và f// = 25 kHz
-
C.
fnt = 5 kHz và f// = 2,4 kHz
-
D.
fnt = 25 kHz và f// = 5,76 kHz
Một tụ điện có điện dung C được nạp điện tới điện tích q. Khi nối tụ với cuộn cảm thuần có độ tự cảm L1 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực đại bằng 70mA. Khi nối tụ với cuộn cảm thuần có độ tự cảm L2 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực dại bằng 35mA. Nếu nối tụ với cuộn cảm thuần có độ tự cảm ${L_3} = 13{L_1} + 9{L_2}$ thì trong mạch có cường độ dòng điện cực đại bằng
-
A.
10mA
-
B.
15mA
-
C.
13mA
-
D.
12mA
Gọi A và vM lần lượt là biên độ và vận tốc cực đại của một chất điểm dao động điều hòa; Q0 và I0 lần lượt là điện tích cực đại trên một bản tụ điện và cường độ dòng điện cực đại trong mạch dao động LC đang hoạt động. Biểu thức \(\frac{{{v_M}}}{A}\) có cùng đơn vị với biểu thức
-
A.
\(\dfrac{{{I_0}}}{{{Q_0}}}\)
-
B.
\({Q_0}I_0^2\)
-
C.
\(\dfrac{{{Q_0}}}{{{I_0}}}\)
-
D.
\({I_0}Q_0^2\)
Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần và tụ điện có điện dung thay đổi được. Khi điện dung của tụ điện có giá trị \(20 pF\) thì chu kì dao động riêng của mạch dao động là \(2,0 µs\). Khi điện dung của tụ điện có giá trị \(80 pF\) thì chu kì dao động riêng của mạch dao động là
-
A.
\(1,0 µs\).
-
B.
\(8,0 µs\).
-
C.
\(4,0 µs\).
-
D.
\(0,5 µs\).
Hai mạch dao động điện từ lí tưởng đang có dao động điện từ tự do với cùng cường độ dòng điện cực đại I0. Chu kì dao động riêng của mạch thứ nhất là T1, của mạch thứ hai là T2 = 2T1. Khi cường độ dòng điện trong hai mạch có cùng độ lớn và nhỏ hơn I0 thì độ lớn điện tích trên một bản tụ điện của mạch dao động thứ nhất là q1 và của mạch dao động thứ hai là q2. Tỉ số \(\dfrac{{{q_1}}}{{{q_2}}}\) là
-
A.
2
-
B.
1,5
-
C.
0,5
-
D.
3
Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Mạch dao động tự do với tần số là
-
A.
\(f = \frac{1}{{2\pi \sqrt {LC} }}\)
-
B.
\(f = \frac{1}{{\sqrt {LC} }}\)
-
C.
\(f = 2\pi \sqrt {LC} \)
-
D.
\(f = \sqrt {LC} \)
Đề thi thử THPT chuyên Lam Sơn - 2021
Một mạch dao động lí tưởng gồm cuộn dây thuần cảm có độ tự cảm L không đổi và tụ điện có điện dung C thay đổi được. Khi điện dung của tụ là \({C_1}\) thì chu kì dao động của mạch là \({3.10^{ - 8}}s\). Từ giá trị \({C_1}\) nếu điều chỉnh tăng thêm điện dung của tụ một lượng \(\Delta C\) thì chu kì dao động riêng của mạch là \({6.10^{ - 8}}s\). Từ giá trị \({C_1}\) nếu điều chỉnh tăng thêm điện dung của tụ một lượng \(9\Delta {C_1}\) thì chu kì dao động riêng của mạch là
-
A.
\(9,{3.10^{ - 8}}s.\)
-
B.
\(15,{9.10^{ - 8}}s.\)
-
C.
\(\dfrac{{40}}{3}{.10^{ - 8}}s.\)
-
D.
\(\dfrac{2}{3}{.10^{ - 8}}s.\)
Một mạch dao động điện từ LC gồm cuộn dây thuần cảm có độ tự cảm L không đổi và tụ điện có C thay đổi được.Biết điện trở của dây dẫn là không đáng kể và trong mạch có dao động điện từ riêng. Khi điện dung có giá trị C1 thì tần số dao động riêng của mạch là f1. Khi điện dung có giá trị \({C_2} = 4{C_1}\) thì tần số dao động điện từ riêng trong mạch là
-
A.
\({f_2} = 2{f_1}\)
-
B.
\({f_2} = \dfrac{{{f_1}}}{2}\)
-
C.
\({f_2} = \dfrac{{{f_1}}}{4}\)
-
D.
\({f_2} = 4{f_1}\)
Lời giải và đáp án
Mạch dao động điện từ điều hoà có cấu tạo gồm
-
A.
Nguồn điện một chiều và tụ điện mắc thành mạch kín.
-
B.
Nguồn điện một chiều và cuộn cảm mắc thành mạch kín.
-
C.
Nguồn điện một chiều và điện trở mắc thành mạch kín.
-
D.
Tụ điện và cuộn cảm mắc thành mạch kín.
Đáp án : D
Mạch dao động LC bao gồm một tụ điện có điện dung C và cuộn cảm có độ tự cảm L tạo thành mạch kín, gọi là mạch dao động hay khung dao động.
Dao động điện từ tự do trong mạch dao động LC được hình thành là do hiện tượng nào sau đây?
-
A.
Hiện tượng cảm ứng điện từ.
-
B.
Hiện tượng cộng hưởng điện.
-
C.
Hiện tượng tự cảm.
-
D.
Hiện tượng từ hóa.
Đáp án : C
Xem lí thuyết mục 1- phần I - Bài Mạch dao động LC
Dao động điện từ tự do trong mạch dao động LC được hình thành là do hiện tượng tự cảm
Mạch dao động điện từ gồm tụ điện C và cuộn cảm L, dao động tự do với tần số góc
-
A.
\(\omega = 2\pi \sqrt {LC} \)
-
B.
\(\omega = \frac{{2\pi }}{{\sqrt {LC} }}\)
-
C.
\(\omega = \sqrt {LC} \)
-
D.
\(\omega = \frac{1}{{\sqrt {LC} }}\)
Đáp án : D
Xem lí thuyết mục 1- phần I - Bài Mạch dao động LC
Tần số góc của dao động điện từ tự do được xác định bằng biểu thức: \(\omega = \frac{1}{{\sqrt {LC} }}\)
Mạch dao động điện từ điều hoà LC có chu kỳ
-
A.
Phụ thuộc vào L, không phụ thuộc vào C.
-
B.
Phụ thuộc vào C, không phụ thuộc vào L.
-
C.
Phụ thuộc vào cả L và C.
-
D.
Không phụ thuộc vào L và C.
Đáp án : C
Vận dụng biểu thức xác định chu kì dao động của mạch dao động điện từ LC: $T = 2\pi \sqrt {LC} $
Ta có, chu kì dao động của mạch LC dao động tự do: $T = 2\pi \sqrt {LC} $
=> Chu kì T phụ thuộc vào L và C
Mạch dao động điện từ điều hoà gồm cuộn cảm L và tụ điện C, khi tăng điện dung của tụ điện lên 4 lần thì chu kỳ dao động của mạch
-
A.
Tăng lên 4 lần.
-
B.
Tăng lên 2 lần.
-
C.
Giảm đi 4 lần.
-
D.
Giảm đi 2 lần.
Đáp án : B
Vận dụng biểu thức xác định chu kì dao động của mạch dao động điện từ LC: $T = 2\pi \sqrt {LC} $
Ta có, chu kì dao động của mạch LC dao động tự do: $T = 2\pi \sqrt {LC} $
=> Khi tăng C lên 4 lần thì chu kì dao động sẽ tăng lên 2 lần
Mạch dao động điện từ điều hoà gồm cuộn cảm L và tụ điện C. Khi tăng độ tự cảm của cuộn cảm lên 2 lần và giảm điện dung của tụ điện đi 2 lần thì tần số dao động của mạch
-
A.
Không đổi.
-
B.
Tăng 2 lần.
-
C.
Giảm 2 lần.
-
D.
Tăng 4 lần.
Đáp án : A
Vận dụng biểu thức xác định tần số dao động của mạch dao động điện từ LC: $f = \frac{1}{{2\pi \sqrt {LC} }}$
Ta có, tần số dao động của mạch LC dao động tự do: $f = \frac{1}{{2\pi \sqrt {LC} }}$
=> Khi tăng L lên 2 lần, điện dung C giảm 2 lần => thì tần số của dao động không đổi
Cường độ dòng điện tức thời trong mạch dao động LC có dạng i = 0,05sin2000t(A). Tần số góc dao động của mạch là
-
A.
318,5 rad/s.
-
B.
318,5 H.
-
C.
2000 rad/s.
-
D.
2000 Hz.
Đáp án : C
Đọc phương trình cường độ dòng điện trong mạch dao động LC
Từ phương trình cường độ dòng điện trong mạch dao động LC i = 0,05sin2000t(A).
Ta có, ω = 2000 (rad/s)
Mạch dao động LC gồm cuộn cảm có độ tự cảm L = 2mH và tụ điện có điện dung C = 2pF, (lấy π2 = 10). Tần số dao động của mạch là:
-
A.
f = 2,5Hz.
-
B.
f = 2,5MHz
-
C.
f = 1Hz.
-
D.
f = 1MHz.
Đáp án : B
Áp dụng biểu thức xác định tần số dao động của mạch dao động điện từ LC: $f = \frac{1}{{2\pi \sqrt {LC} }}$
Ta có, tần số dao động của mạch LC dao động tự do: $f = \frac{1}{{2\pi \sqrt {LC} }} = \frac{1}{{2\pi \sqrt {{{2.10}^{ - 3}}{{.2.10}^{ - 12}}} }} = {2,5.10^6}H{\rm{z}}$
Mạch dao động điện từ gồm tụ điện C = 16nF và cuộn cảm L = 25mH. Tần số góc dao động của mạch là:
-
A.
ω = 200Hz.
-
B.
ω = 200rad/s.
-
C.
ω = 5.10-5
-
D.
ω = 5.104rad/s.
Đáp án : D
Áp dụng biểu thức xác định tần số góc của mạch dao động điện từ LC: $\omega = \frac{1}{{\sqrt {LC} }}$
Ta có, tần số góc của mạch LC dao động tự do: $\omega = \frac{1}{{\sqrt {LC} }} = \frac{1}{{\sqrt {{{25.10}^{ - 3}}{{.16.10}^{ - 9}}} }} = {5.10^4}(ra{\rm{d}}/s)$
Cường độ dòng điện tức thời trong mạch dao động LC có dạng $i= 0,02cos2000t(A)$. Tụ điện trong mạch có điện dung $5μF$. Độ tự cảm của cuộn cảm là:
-
A.
L = 50mH
-
B.
L = 50H
-
C.
L = 5.10-6H
-
D.
L = 5.10-8H
Đáp án : A
+ Đọc phương trình cường độ dòng điện trong mạch LC
+ Áp dụng biểu thức xác định tần số góc của mạch dao động LC: $\omega = \frac{1}{{\sqrt {LC} }}$
Từ phương trình cường độ dòng điện $i = 0,02cos2000t(A)$
Ta có: $ω = 2000 (rad/s)$
Mặt khác, ta có: $\omega = \dfrac{1}{{\sqrt {LC} }} \to L = \dfrac{1}{{{\omega ^2}C}} = \dfrac{1}{{{{2000}^2}{{.5.10}^{ - 6}}}} = 0,05H$
Mạch dao động LC có điện tích trong mạch biến thiên điều hoà theo phương trình \(q = 4cos(2π.10^4t)μC\) . Tần số dao động của mạch là:
-
A.
f = 10(Hz).
-
B.
f = 10(kHz).
-
C.
f = 2π(Hz).
-
D.
f = 2π(kHz).
Đáp án : B
Áp dụng biểu thức xác định tần số dao động của mạch dao động điện từ LC: $f = \frac{1}{{2\pi \sqrt {LC} }}$
Từ phương trình điện tích: q = 4cos(2π.104t)μC
=> ω = 2π.104
Mặt khác, ta có: $\omega = 2\pi f \to f = \frac{\omega }{{2\pi }} = \frac{{2\pi {{.10}^4}}}{{2\pi }} = {10^4}(H{\text{z}})$
Trong mạch dao động điện từ tự do LC, so với dòng điện trong mạch thì điện áp giữa hai bản tụ điện luôn:
-
A.
Cùng pha.
-
B.
Trễ pha hơn một góc π/2.
-
C.
Sớm pha hơn một góc π/4.
-
D.
Sớm pha hơn một góc π/2.
Đáp án : B
Trong mạch dao động điện từ tự do LC, điện áp giữa hai bản tụ điện luôn trễ pha hơn dòng điện trong mạch một góc π/2
Mạch dao động điện từ dao động tự do với tần số góc ω. Biết điện tích cực đại trên tụ điện là q0. Cường độ dòng điện đi qua cuộn dây thuần cảm có giá trị cực đại là:
-
A.
I0 = ω q0.
-
B.
I0 = ω2 q0
-
C.
I0 = 2ω q0.
-
D.
I0 = ω.q02.
Đáp án : A
Xem lí thuyết mục 1
Cường độ dòng điện cực đại trong mạch: I0 = ωq0
Gọi U0 là điện áp cực đại giữa hai đầu bản tụ điện, I0 là cường độ dòng điện cực đại đi qua cuộn cảm. Biểu thức liên hệ giữa U0 và I0 của mạch dao động LC là:
-
A.
\({I_0} = {\text{ }}{U_0}\sqrt {\dfrac{C}{L}} \)
-
B.
\({U_0} = {\text{ }}{I_0}\sqrt {\dfrac{C}{L}} \)
-
C.
\({U_0} = {\text{ }}{I_0}\sqrt {LC} \)
-
D.
\({I_0} = {\text{ }}{U_0}\sqrt {LC} \)
Đáp án : A
Cường độ dòng điện cực đại trong mạch: \({I_0} = \omega {q_0} = \dfrac{{{q_0}}}{{\sqrt {LC} }} = \dfrac{{{U_0}C}}{{\sqrt {LC} }} = {U_0}\sqrt {\dfrac{C}{L}} \)
Một mạch dao động gồm cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C. Nếu gọi I0 là cường độ dòng điện cực đại trong mạch, thì hệ thức liên hệ điện tích cực đại trên bản tụ điện q0 và I0 là:
-
A.
\({q_0} = \sqrt {\frac{{CL}}{\pi }} {I_0}\)
-
B.
\({q_0} = {I_0}\sqrt {LC}\)
-
C.
\({q_0} = \sqrt {\frac{C}{{\pi L}}} {I_0}\)
-
D.
\({q_0} = \sqrt {\frac{1}{{CL}}} {I_0}\)
Đáp án : B
Xem lí thuyết mục 1
Cường độ dòng điện cực đại trong mạch: \({I_0} = \omega {q_0} \to {q_0} = \dfrac{{{I_0}}}{\omega } = \frac{{{I_0}}}{{\dfrac{1}{{\sqrt {LC} }}}} = {I_0}\sqrt {LC} \)
Mạch dao động điện từ điều hoà LC gồm tụ điện C = 30nF và cuộn cảm L =25mH. Nạp điện cho tụ điện đến hiệu điện thế 4,8V rồi cho tụ phóng điện qua cuộn cảm, cường độ dòng điện hiệu dụng trong mạch là:
-
A.
I = 3,72mA.
-
B.
I = 4,28mA.
-
C.
I = 5,20mA.
-
D.
I = 6,34mA.
Đáp án : A
Áp dụng biểu thức mối liên hệ giữa cường độ dòng điện cực đại và hiệu điện thế cực đại trong mạch dao động LC: \({I_0} = {U_0}\sqrt {\frac{C}{L}} \)
Ta có:
Cường độ dòng điện cực đại trong mạch: \({I_0} = \omega {q_0} = \frac{{{q_0}}}{{\sqrt {LC} }} = \frac{{{U_0}C}}{{\sqrt {LC} }} = {U_0}\sqrt {\frac{C}{L}} \)
=> Cường độ dòng điện hiệu dụng trong mạch: \(I = U\sqrt {\frac{C}{L}} = \frac{{{U_0}}}{{\sqrt 2 }}\sqrt {\frac{C}{L}} = \frac{{4,8}}{{\sqrt 2 }}\sqrt {\frac{{{{30.10}^{ - 9}}}}{{{{25.10}^{ - 3}}}}} = 3,{72.10^{ - 3}}A = 3,72mA\)
Một mạch dao động gồm một tụ điện có điện dung C = 18 nF và một cuộn dây thuần cảm có độ tự cảm L = 6 μH. Điện áp cực đại ở hai đầu tụ điện là 4V, cường độ dòng điện cực đại trong mạch là:
-
A.
87,2 mA.
-
B.
219 mA.
-
C.
12 mA.
-
D.
21,9 mA
Đáp án : B
Áp dụng biểu thức mối liên hệ giữa cường độ dòng điện cực đại và hiệu điện thế cực đại trong mạch dao động LC: \({I_0} = {U_0}\sqrt {\frac{C}{L}} \)
Ta có:
Cường độ dòng điện cực đại trong mạch: \({I_0} = {U_0}\sqrt {\frac{C}{L}} = 4.\sqrt {\frac{{{{18.10}^{ - 9}}}}{{{{6.10}^{ - 6}}}}} = 0,219A = 219mA\)
Nhận xét nào sau đây về đặc điểm của mạch dao động điện từ điều hoà LC là không đúng?
-
A.
Điện tích trong mạch biến thiên điều hoà.
-
B.
Năng lượng điện trường tập trung chủ yếu ở tụ điện.
-
C.
Năng lượng từ trường tập trung chủ yếu ở cuộn cảm.
-
D.
Tần số dao động của mạch phụ thuộc vào điện tích của tụ điện.
Đáp án : D
Xem lí thuyết phần I - Nội dung lí thuyết
A, B, C - đúng
D - sai vì: tần số dao động của mạch: $f = \frac{1}{{2\pi \sqrt {LC} }}$
Khi mắc tụ điện có điện dung C1 với cuộn cảm L thì tần số dao động của mạch là f1, khi mắc tụ điện có điện dung C2 với cuộn cảm L thì tần số dao động của mạch là f2. Khi mắc song song C1 với C2 và mắc với cuộn cảm L thì tần số dao động của mạch là:
-
A.
$\dfrac{1}{{f_{//}^2}} = \dfrac{1}{{f_1^2}} + \dfrac{1}{{f_2^2}}$
-
B.
$f_{//}^2 = f_1^2 + f_2^2{\text{ }}$
-
C.
$\dfrac{1}{{f_{//}^2}} = \dfrac{1}{{f_1^2}} - \dfrac{1}{{f_2^2}}$
-
D.
$f_{//}^2 = f_1^2 - f_2^2$
Đáp án : A
- Khi mắc tụ điện có điện dung C1 thì tần số dao động của mạch là f1
- Khi mắc tụ điện có điện dung C2 thì tần số dao động của mạch là f2
- Khi mắc song song C1 và C2 thì tần số dao động của mạch là: $\dfrac{1}{{f_{//}^2}} = \dfrac{1}{{f_1^2}} + \dfrac{1}{{f_2^2}}$
Khi mắc tụ điện có điện dung C1 với cuộn cảm L thì tần số dao động của mạch là f1, khi mắc tụ điện có điện dung C2 với cuộn cảm L thì tần số dao động của mạch là f2. Khi mắc C1 nối tiếp với C2 và mắc với cuộn cảm L thì tần số dao động của mạch là:
-
A.
$\frac{1}{{f_{nt}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}}$
-
B.
$f_{nt}^2 = f_1^2 + f_2^2{\text{ }}$
-
C.
$\frac{1}{{f_{nt}^2}} = \frac{1}{{f_1^2}} - \frac{1}{{f_2^2}}$
-
D.
$f_{nt}^2 = f_1^2 - f_2^2$
Đáp án : B
Xem lí thuyết mục 1- phần II - Các dạng bài tập
- Khi mắc tụ điện có điện dung C1 thì tần số dao động của mạch là f1
- Khi mắc tụ điện có điện dung C2 thì tần số dao động của mạch là f2
- Khi mắc nối tiếp C1 và C2 thì tần số dao động của mạch là: $f_{nt}^2 = f_1^2 + f_2^2{\text{ }}$
Khi mắc tụ điện có điện dung C1 với cuộn cảm có độ tự cảm L thì tần số dao động của mạch là f1 = 6kHz; khi mắc tụ điện có điện dung C2 với cuộn cảm có độ tự cảm L thì tần số dao động của mạch là f2 = 8kHz. Khi mắc C1 song song C2 với cuộn cảm có độ tự cảm L thì tần số dao động của mạch là bao nhiêu?
-
A.
f = 4,8kHz.
-
B.
f = 7kHz.
-
C.
f = 10kHz.
-
D.
f = 14kHz.
Đáp án : A
Áp dụng biểu thức xác định tần số dao động của mạch khi ghép song song tụ C1 và C2: $\frac{1}{{f_{//}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}}$
Ta có:
- Khi mắc tụ điện có điện dung C1 thì tần số dao động của mạch là f1
- Khi mắc tụ điện có điện dung C2 thì tần số dao động của mạch là f2
- Khi mắc song song C1 và C2 thì tần số dao động của mạch là:
$\frac{1}{{f_{//}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}} = \frac{{f_1^2 + f_2^2}}{{f_1^2f_2^2}} \to {f_{//}} = \frac{{{f_1}{f_2}}}{{\sqrt {f_1^2 + f_2^2} }} = \frac{{{{6.10}^3}{{.8.10}^3}}}{{\sqrt {{{({{6.10}^3})}^2} + {{({{8.10}^3})}^2}} }} = 4,{8.10^3}H{\text{z}} = 4,8kH{\text{z}}$
Khi mắc tụ điện có điện dung C1 với cuộn cảm L thì chu kì dao động của mạch là T1 = 2 ms; khi mắc tụ điện có điện dung C2 với cuộn L thì chu kì dao động của mạch là T2 = 1,5 ms. Khi mắc nối tiếp C1 và C2 với cuộn L thì chu kì dao động của mạch là bao nhiêu?
-
A.
T = 0,694 ms
-
B.
T= 0,857 ms.
-
C.
T = 1,2 ms.
-
D.
T = 1,44 ms.
Đáp án : C
Áp dụng biểu thức xác định chu kì dao động của mạch khi ghép nối tiếp tụ C1 và C2: $\frac{1}{{T_{nt}^2}} = \frac{1}{{T_1^2}} + \frac{1}{{T_2^2}}$
Ta có:
- Khi mắc tụ điện có điện dung C1 thì chu kì dao động của mạch là T1
- Khi mắc tụ điện có điện dung C2 thì chu kì dao động của mạch là T2
- Khi mắc nối tiếp C1 và C2 thì chu kì dao động của mạch là:
$\frac{1}{{T_{nt}^2}} = \frac{1}{{T_1^2}} + \frac{1}{{T_2^2}} = \frac{{T_1^2 + T_2^2}}{{T_1^2T_2^2}} \to {T_{nt}} = \frac{{{T_1}{T_2}}}{{\sqrt {T_1^2 + T_2^2} }} = \frac{{({{2.10}^{ - 3}}).(1,{{5.10}^{ - 3}})}}{{\sqrt {{{({{2.10}^{ - 3}})}^2} + {{(1,{{5.10}^{ - 3}})}^2}} }} = 1,{2.10^{ - 3}}s = 1,2m{\text{s}}$
Khi mắc cuộn cảm có độ tự cảm L1 với tụ điện có điện dung C thì tần số dao động của mạch là f1, khi mắc cuộn cảm có độ tự cảm L2 với tụ điện có điện dung C thì tần số dao động của mạch là f2. Nhận định nào sau đây là đúng:
-
A.
Khi mắc L1 nối tiếp L2: $f_{nt}^2 = f_1^2 + f_2^2{\text{ }}$
-
B.
Khi mắc L1 song song L2: $T_{//}^2 = T_1^2 + T_2^2{\text{ }}$
-
C.
Khi mắc L1 nối tiếp L2: $T_{nt}^2 = T_1^2 + T_2^2$
-
D.
Khi mắc L1 song song L2: $\frac{1}{{f_{//}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}}$
Đáp án : C
Xem lí thuyết mục 1- phần II - Các dạng bài tập
Ta có:
Mạch gồm L1 và C có tần số f1 - Mạch gồm L2 và C có tần số f2
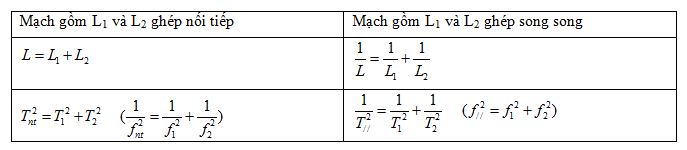
Khi mắc cuộn cảm có độ tự cảm L1 với tụ điện có điện dung C thì tần số dao động của mạch là f1 = 3 kHz, khi mắc cuộn cảm có độ tự cảm L2 với tụ điện có điện dung C thì tần số dao động của mạch là f2= 4 kHz. Tần số dao động của mạch khi mắc L1 nối tiếp với L2 và tần số dao động của mạch khi mắc L1 song song L2 là:
-
A.
fnt = 2,4 kHz và f// = 5 kHz
-
B.
fnt = 5,76 kHz và f// = 25 kHz
-
C.
fnt = 5 kHz và f// = 2,4 kHz
-
D.
fnt = 25 kHz và f// = 5,76 kHz
Đáp án : A
+ Áp dụng biểu thức xác định tần số dao động của mạch khi ghép nối tiếp cuộn cảm có độ tự cảm L1 và L2: $\frac{1}{{f_{nt}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}}$
+ Áp dụng biểu thức xác định tần số dao động của mạch khi ghép song song cuộn cảm có độ tự cảm L1 và L2: $f_{//}^2 = f_1^2 + f_2^2$
Ta có:
- Khi mắc cuộn cảm có độ tự cảm L1 thì tần số dao động của mạch là f1
- Khi mắc cuộn cảm có độ tự cảm L2 thì tần số dao động của mạch là f2
- Khi mắc nối tiếp L1 và L2 thì tần số dao động của mạch là:
$\frac{1}{{f_{nt}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}} = \frac{{f_1^2 + f_2^2}}{{f_1^2f_2^2}} \to {f_{nt}} = \frac{{{f_1}{f_2}}}{{\sqrt {f_1^2 + f_2^2} }} = \frac{{{{3.10}^3}{{.4.10}^3}}}{{\sqrt {{{({{3.10}^3})}^2} + {{({{4.10}^3})}^2}} }} = 2,{4.10^3}H{\text{z}} = 2,4kH{\text{z}}$
- Khi mắc song song L1 và L2 thì tần số dao động của mạch là:
$f_{//}^2 = f_1^2 + f_2^2 \to {f_{//}} = \sqrt {f_1^2 + f_2^2} = \sqrt {{{({{3.10}^3})}^2} + {{\left( {{{4.10}^3}} \right)}^2}} = {5.10^3}H{\text{z}} = 5kH{\text{z}}$
Một tụ điện có điện dung C được nạp điện tới điện tích q. Khi nối tụ với cuộn cảm thuần có độ tự cảm L1 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực đại bằng 70mA. Khi nối tụ với cuộn cảm thuần có độ tự cảm L2 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực dại bằng 35mA. Nếu nối tụ với cuộn cảm thuần có độ tự cảm ${L_3} = 13{L_1} + 9{L_2}$ thì trong mạch có cường độ dòng điện cực đại bằng
-
A.
10mA
-
B.
15mA
-
C.
13mA
-
D.
12mA
Đáp án : A
+ Áp dụng biểu thức tính cường độ dòng điện cực đại: I0 = ωq0
+ Áp dụng biểu thức xác định tần số góc của mạch dao động LC: $\omega = \frac{1}{{\sqrt {LC} }}$
Cách 1 :
Ta có:
\(\begin{array}{l}{I_1} = {\omega _1}q = \frac{q}{{\sqrt {{L_1}C} }} = > {L_1} = \frac{{{q^2}}}{{{I_1}^2C}}\\{I_2} = {\omega _2}q = \frac{q}{{\sqrt {{L_2}C} }} = > {L_2} = \frac{{{q^2}}}{{{I_2}^2C}}\end{array}\)
=> Khi sử dụng cuộn cảm có độ tự cảm \({L_3} = 13{L_1} + 9{L_2}\) thì cường độ dòng điện cực đại là :
\({I_3} = \frac{q}{{\sqrt {{L_3}C} }} = \frac{q}{{\sqrt {(13\frac{{{q^2}}}{{{I_1}^2C}} + 9\frac{{{q^2}}}{{{I_2}^2C}})C} }} = \frac{{{I_1}{I_2}}}{{\sqrt {13{I_2}^2 + 9{I_1}^2} }} = 10mA\)
Cách 2:
Ta có:
\(\begin{array}{l}{I_1} = {\omega _1}q = \frac{q}{{\sqrt {{L_1}C} }};{I_2} = {\omega _2}q = \frac{q}{{\sqrt {{L_2}C} }}\\ \to \frac{{{I_1}}}{{{I_2}}} = \sqrt {\frac{{{L_2}}}{{{L_1}}}} = \frac{{70}}{{35}} \to \frac{{{L_2}}}{{{L_1}}} = 4\\ \to {L_2} = 4{L_1}\end{array}\)
\(\begin{array}{l}{I_3} = \frac{q}{{\sqrt {{L_3}C} }} \to \frac{{{I_3}}}{{{I_1}}} = \sqrt {\frac{{{L_1}}}{{{L_3}}}} = \sqrt {\frac{{{L_1}}}{{13{L_1} + 9{L_2}}}} = \sqrt {\frac{{{L_1}}}{{13{L_1} + 9.4{L_1}}}} = \frac{1}{7}\\ \to {I_3} = \frac{{{I_1}}}{7} = \frac{{70}}{7} = 10mA\end{array}\)
Gọi A và vM lần lượt là biên độ và vận tốc cực đại của một chất điểm dao động điều hòa; Q0 và I0 lần lượt là điện tích cực đại trên một bản tụ điện và cường độ dòng điện cực đại trong mạch dao động LC đang hoạt động. Biểu thức \(\frac{{{v_M}}}{A}\) có cùng đơn vị với biểu thức
-
A.
\(\dfrac{{{I_0}}}{{{Q_0}}}\)
-
B.
\({Q_0}I_0^2\)
-
C.
\(\dfrac{{{Q_0}}}{{{I_0}}}\)
-
D.
\({I_0}Q_0^2\)
Đáp án : A
Vận dụng các đơn vị của các đại lượng và biểu thức liên hệ giữa chúng
Ta có: \(\left\{ \begin{array}{l}\dfrac{{{v_M}}}{A}\left[ {\dfrac{{m/s}}{m} = \dfrac{1}{s}} \right]\\\dfrac{{{I_0}}}{{{Q_0}}}\left[ {\dfrac{A}{{A.s}} = \dfrac{1}{s}} \right]\end{array} \right.\)
Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần và tụ điện có điện dung thay đổi được. Khi điện dung của tụ điện có giá trị \(20 pF\) thì chu kì dao động riêng của mạch dao động là \(2,0 µs\). Khi điện dung của tụ điện có giá trị \(80 pF\) thì chu kì dao động riêng của mạch dao động là
-
A.
\(1,0 µs\).
-
B.
\(8,0 µs\).
-
C.
\(4,0 µs\).
-
D.
\(0,5 µs\).
Đáp án : C
Chu kì của dao động mạch dao động điện từ LC:\(T = 2\pi \sqrt {LC} \)
Ta có chu kì của dao động mạch dao động điện từ LC:\(T = 2\pi \sqrt {LC} \)
\(\dfrac{{{T_1}}}{{{T_2}}} = \sqrt {\dfrac{{{C_1}}}{{{C_2}}}} \Leftrightarrow \dfrac{2}{{{T_2}}} = \sqrt {\dfrac{{20}}{{80}}} \)
\( \Leftrightarrow \dfrac{2}{{{T_2}}} = \dfrac{1}{2} \Leftrightarrow {T_2} = 4\mu s\)
Hai mạch dao động điện từ lí tưởng đang có dao động điện từ tự do với cùng cường độ dòng điện cực đại I0. Chu kì dao động riêng của mạch thứ nhất là T1, của mạch thứ hai là T2 = 2T1. Khi cường độ dòng điện trong hai mạch có cùng độ lớn và nhỏ hơn I0 thì độ lớn điện tích trên một bản tụ điện của mạch dao động thứ nhất là q1 và của mạch dao động thứ hai là q2. Tỉ số \(\dfrac{{{q_1}}}{{{q_2}}}\) là
-
A.
2
-
B.
1,5
-
C.
0,5
-
D.
3
Đáp án : C
Điện tích cực đại trên một bản tụ: \({Q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{{I_0}T}}{{2\pi }}\)
Công thức độc lập với thời gian: \(\dfrac{{{i^2}}}{{{I_0}^2}} + \dfrac{{{q^2}}}{{{Q_0}^2}} = 1\)
Theo đề bài ta có: \({T_2} = 2{T_1} \Rightarrow {Q_{02}} = 2{Q_{01}}\)
Áp dụng công thức độc lập với thời gian cho hai mạch, ta có:
\(\left\{ \begin{array}{l}\dfrac{{{i^2}}}{{{I_0}^2}} + \dfrac{{{q_1}^2}}{{{Q_{01}}^2}} = 1\\\dfrac{{{i^2}}}{{{I_0}^2}} + \dfrac{{{q_2}^2}}{{{Q_{02}}^2}} = 1\end{array} \right. \Rightarrow \dfrac{{{q_1}^2}}{{{Q_{01}}^2}} = \dfrac{{{q_2}^2}}{{{Q_{02}}^2}} \Rightarrow \dfrac{{{q_1}}}{{{q_2}}} = \dfrac{{{Q_{01}}}}{{{Q_{02}}}} = 0,5\)
Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Mạch dao động tự do với tần số là
-
A.
\(f = \frac{1}{{2\pi \sqrt {LC} }}\)
-
B.
\(f = \frac{1}{{\sqrt {LC} }}\)
-
C.
\(f = 2\pi \sqrt {LC} \)
-
D.
\(f = \sqrt {LC} \)
Đáp án : A
Sử dụng biểu thức tính tần số dao động mạch LC: \(f = \frac{1}{{2\pi \sqrt {LC} }}\)
Tần số dao động mạch LC: \(f = \frac{1}{{2\pi \sqrt {LC} }}\)
Đề thi thử THPT chuyên Lam Sơn - 2021
Một mạch dao động lí tưởng gồm cuộn dây thuần cảm có độ tự cảm L không đổi và tụ điện có điện dung C thay đổi được. Khi điện dung của tụ là \({C_1}\) thì chu kì dao động của mạch là \({3.10^{ - 8}}s\). Từ giá trị \({C_1}\) nếu điều chỉnh tăng thêm điện dung của tụ một lượng \(\Delta C\) thì chu kì dao động riêng của mạch là \({6.10^{ - 8}}s\). Từ giá trị \({C_1}\) nếu điều chỉnh tăng thêm điện dung của tụ một lượng \(9\Delta {C_1}\) thì chu kì dao động riêng của mạch là
-
A.
\(9,{3.10^{ - 8}}s.\)
-
B.
\(15,{9.10^{ - 8}}s.\)
-
C.
\(\dfrac{{40}}{3}{.10^{ - 8}}s.\)
-
D.
\(\dfrac{2}{3}{.10^{ - 8}}s.\)
Đáp án : B
Chu kì dao động của mạch dao động: \(T = 2\pi \sqrt {LC} \)
+ Khi \(C = {C_1}\) có: \({T_1} = 2\pi \sqrt {L{C_1}} = {3.10^{ - 8}}s\)
+ Khi \(C = {C_1} + \Delta C\)có: \({T_2} = 2\pi \sqrt {L\left( {{C_1} + \Delta C} \right)} = {6.10^{ - 8}}s\)
\( \Rightarrow \frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{{C_1}}}{{{C_1} + \Delta C}}} \Leftrightarrow \frac{3}{6} = \sqrt {\frac{{{C_1}}}{{{C_1} + \Delta C}}} \Rightarrow \Delta C = 3{C_1}\)
+ Khi \(C = {C_1} + 9\Delta C\)có: \(T = 2\pi \sqrt {L\left( {{C_1} + 9\Delta C} \right)} \)
\( \Rightarrow T = 2\pi \sqrt {L\left( {{C_1} + 9.3{C_1}} \right)} = 2\pi \sqrt {28L{C_1}} = 2\sqrt 7 {T_1} = 15,{87.10^{ - 3}}s\)
Một mạch dao động điện từ LC gồm cuộn dây thuần cảm có độ tự cảm L không đổi và tụ điện có C thay đổi được.Biết điện trở của dây dẫn là không đáng kể và trong mạch có dao động điện từ riêng. Khi điện dung có giá trị C1 thì tần số dao động riêng của mạch là f1. Khi điện dung có giá trị \({C_2} = 4{C_1}\) thì tần số dao động điện từ riêng trong mạch là
-
A.
\({f_2} = 2{f_1}\)
-
B.
\({f_2} = \dfrac{{{f_1}}}{2}\)
-
C.
\({f_2} = \dfrac{{{f_1}}}{4}\)
-
D.
\({f_2} = 4{f_1}\)
Đáp án : B
Sử dụng công thức: \(f = \dfrac{1}{{2\pi \sqrt {LC} }}\)
Ta có:
\(\left\{ \begin{array}{l}{f_1} = \frac{1}{{2\pi \sqrt {L{C_1}} }}\\{f_2} = \frac{1}{{2\pi \sqrt {L4{C_1}} }}\end{array} \right. \Leftrightarrow \frac{{{f_1}}}{{{f_2}}} = \frac{{2\pi \sqrt {L4{C_1}} }}{{2\pi \sqrt {L{C_1}} }} = 2\)
\( \Rightarrow {f_2} = \frac{{{f_1}}}{2}\)
Luyện tập và củng cố kiến thức Bài 20. Bài tập năng lượng của mạch dao dộng LC Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 20. Các loại dao động Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 20. Phương trình dao động mạch LC (q - u - i) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 21. Điện từ trường Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 22. Sóng điện từ Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 23. Nguyên tắc thông tin liên lạc bằng sóng vô tuyến Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập dao động và sóng điện từ (phần 1) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập năng lượng dao động điện từ (phần 2) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập chương 4 Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết










Danh sách bình luận