-
Chương 1. Dao động cơ
- Bài 1. Dao động điều hòa
- Bài 1. Dao động điều hòa - Các đại lượng đặc trưng
- Bài 1. Viết phương trình dao động điều hòa
- Bài 1. Ứng dụng vòng tròn lượng giác
- Bài 1. Bài tập quãng đường, tốc độ trung bình
- Bài 2. Con lắc lò xo - Bài tập chu kì, tần số, tần số góc của con lắc lò xo
- Bài 2. Năng lượng của con lắc lò xo
- Bài 2. Chiều dài con lắc lò xo
- Bài 2. Thời gian nén - giãn của con lắc lò xo
- Bài 2. Va chạm con lắc lò xo
- Bài 3. Con lắc đơn - Các đại lượng đặc trưng
- Bài 3. Năng lượng, vận tốc - lực của con lắc đơn
- Bài 4. Sự thay đổi chu kì con lắc đơn khi chịu thêm tác dụng của lực lạ
- Bài 4. Sự nhanh chậm của đồng hồ quả lắc
- Bài 4. Con lắc vướng đinh - sự trùng phùng của hai con lắc
- Tổng hợp bài tập các loại dao động
- Tổng hợp bài tập dao động điều hòa
- Tổng hợp bài tập dao động cơ (phần 1)
- Tổng hợp bài tập dao động cơ (phần 2)
- Tổng hợp bài tập dao động cơ (phần 3)
- Ôn tập chương 1
-
Chương 2. Sóng cơ và sóng âm
- Bài 7. Sóng cơ và sự truyền sóng cơ
- Bài 7. Các đại lượng đặc trưng cơ bản của sóng cơ
- Bài 7. Phương trình sóng cơ học
- Bài 7. Đồ thị sóng cơ học
- Bài 8. Giao thoa sóng
- Bài 8. Xác định cực đại - cực tiểu giao thoa sóng
- Bài 8. Phương trình sóng cơ tại một điểm trong trường giao thoa
- Bài 8. Pha dao động tại một điểm trong trường giao thoa
- Bài 9. Sóng dừng
- Bài 10. Sóng âm - Các đặc trưng vật lí và sinh lí của âm
- Tổng hợp bài tập sóng cơ - sóng âm (phần 1)
- Tổng hợp bài tập sóng cơ - sóng âm (phần 2)
- Ôn tập chương 2
-
Chương 3. Dòng điện xoay chiều
- Bài 12. Đại cương về dòng điện xoay chiều
- Bài 12. Bài tập đại cương dòng điện xoay chiều
- Bài 13. Các mạch điện xoay chiều
- Bài 14. Mạch R, L, C mắc nối tiếp
- Bài 14. Bài tập mạch xoay chiều R, L, C
- Bài 15. Công suất điện tiêu thụ của mạch điện xoay chiều - Hệ số công suất
- Tổng hợp bài tập mạch xoay chiều RLC - có R thay đổi
- Tổng hợp bài tập mạch xoay chiều RLC - có C thay đổi
- Tổng hợp bài tập mạch xoay chiều RLC - có L thay đổi
- Tổng hợp bài tập mạch xoay chiều RLC - có ω (hay f, T) thay đổi
- Tổng hợp bài tập mạch xoay chiều RLC - Phương pháp giản đồ
- Tổng hợp bài tập phương pháp Casio (số phức giải điện xoay chiều)
- Tổng hợp bài tập mạch xoay chiều RLC - Bài toán hộp đen
- Bài 16. Truyền tải điện năng - Máy biến áp
- Bài 17. Máy phát điện xoay chiều - Động cơ không đồng bộ ba pha
- Tổng hợp bài tập điện xoay chiều (phần 1)
- Tổng hợp bài tập điện xoay chiều (phần 2)
- Tổng hợp bài tập điện xoay chiều (Phần 3)
- Ôn tập chương 3
-
Chương 4. Dao động và sóng điện từ
- Bài 20. Bài tập mạch dao động LC - Các đại lượng đặc trưng
- Bài 20. Bài tập năng lượng của mạch dao dộng LC
- Bài 20. Các loại dao động
- Bài 20. Phương trình dao động mạch LC (q - u - i)
- Bài 21. Điện từ trường
- Bài 22. Sóng điện từ
- Bài 23. Nguyên tắc thông tin liên lạc bằng sóng vô tuyến
- Tổng hợp bài tập dao động và sóng điện từ (phần 1)
- Tổng hợp bài tập năng lượng dao động điện từ (phần 2)
- Ôn tập chương 4
-
Chương 5. Sóng ánh sáng
- Bài 24. Tán sắc ánh sáng
- Bài 25. Giao thoa ánh sáng
- Tổng hợp bài tập giao thoa ánh sáng đơn sắc
- Tổng hợp bài tập dịch nguồn - Đặt bản mỏng
- Tổng hợp bài tập giao thoa 2 ánh sáng - 3 ánh sáng
- Tổng hợp bài tập tập giao thoa ánh sáng trắng
- Bài 26. Các loại quang phổ
- Bài 27. Các loại tia: Tia hồng ngoại - Tia tử ngoại - Tia X
- Tổng hợp bài tập sóng ánh sáng (phần 1)
- Tổng hợp bài tập sóng ánh sáng (phần 2)
- Ôn tập chương 5
-
Chương 6. Lượng tử ánh sáng
- Bài 30. Hiện tượng quang điện - Thuyết lượng tử ánh sáng
- Tổng hợp bài tập về cường độ dòng quang điện bão hòa và hiệu suất lượng tử
- Bài 31. Hiện tượng quang điện trong
- Bài 32. Hiện tượng quang - phát quang
- Tổng hợp bài tập chuyển động của electron quang điện trong điện trường đều và từ trường đều
- Bài 33. Mẫu nguyên tử Bo
- Bài 34. Sơ lược về laze
- Tổng hợp bài tập lượng tử ánh sáng
- Ôn tập chương 6
-
Chương 7. Hạt nhân nguyên tử
- Bài 35. Tính chất và cấu tạo hạt nhân
- Bài 36. Năng lượng liên kết của hạt nhân
- Bài 36. Phản ứng hạt nhân
- Tổng hợp bài tập xác định động năng, vận tốc, góc của các hạt
- Bài 37. Phóng xạ
- Tổng hợp bài tập về phóng xạ
- Bài 38. Phản ứng phân hạch - nhiệt hạch
- Tổng hợp bài tập hạt nhân nguyên tử (phần 1)
- Tổng hợp bài tập hạt nhân nguyên tử (phần 2)
Trắc nghiệm Bài 1. Dao động điều hòa - Vật Lí 12
Đề bài
Dao động điều hòa là:
-
A.
Dao động trong đó li độ của vật là một hàm tan (hay cotan) của thời gian.
-
B.
Dao động mà vật chuyển động qua lại quanh một vị trí đặc biệt gọi là vị trí cân bằng.
-
C.
Dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.
-
D.
Dao động mà trạng thái của vật được lặp lại như cũ, theo hướng cũ sau những khoảng thời gian bằng nhau xác định.
Một chất điểm dao động điều hòa với phương trình $x = Ac{\rm{os(}}\omega {\rm{t + }}\varphi {\rm{)}}$, trong đó ω có giá trị dương. Đại lượng ω gọi là
-
A.
Biên độ dao động.
-
B.
Chu kì của dao động.
-
C.
Tần số góc của dao động.
-
D.
Pha ban đầu của dao động.
Một chất điểm dao động điều hòa với phương trình $x =Acos(ωt + φ)$; trong đó $A, ω$ là các hằng số dương. Pha của dao động ở thời điểm $t$ là
-
A.
$(\omega t + \varphi )$
-
B.
$ω$
-
C.
$φ$
-
D.
$ωt$
Trong dao động điều hòa của một vật thì tập hợp 2 đại lượng nào sau đây là không đổi theo thời gian?
-
A.
Biên độ, tần số.
-
B.
Biên độ, gia tốc.
-
C.
Vận tốc, tần số.
-
D.
Li độ, vận tốc.
Pha của dao động được dùng để xác định
-
A.
Biên độ dao động
-
B.
Trạng thái dao động
-
C.
Tần số dao động
-
D.
Chu kỳ dao động
Pha ban đầu của dao động điều hòa phụ thuộc
-
A.
Cách chọn gốc tọa độ và gốc thời gian
-
B.
Năng lượng truyền cho vật để vật dao động
-
C.
Đặc tính của hệ dao động
-
D.
Cách kích thích vật dao động
Biên độ dao động:
-
A.
Là quãng đường vật đi trong một chu kỳ dao động
-
B.
Là quãng đường vật đi được trong nửa chu kỳ dao động
-
C.
Là độ dời lớn nhất của vật trong quá trình dao động
-
D.
Là độ dài quỹ đạo chuyển động của vật
Một vật dao động điều hoà dọc theo trục Ox với phương trình: \(x{\text{ }} = {\text{ }}Acos(\pi t){\text{ }}cm\). Nếu chọn gốc toạ độ O tại vị trí cân bằng của vật thì gốc thời gian $t = 0$ là lúc vật:
-
A.
Ở vị trí li độ cực đại thuộc phần dương của trục Ox
-
B.
Qua vị trí cân bằng O ngược chiều dương của trục Ox
-
C.
Ở vị trí li độ cực đại thuộc phần âm của trục Ox
-
D.
Qua vị trí cân bằng O theo chiều dương của trục Ox
Một vật dao động điều hòa theo phương trình li độ $x = 5cosπt (cm)$. Tốc độ cực đại của vật bằng:
-
A.
$π (cm/s)$
-
B.
$5/π (cm/s)$
-
C.
$5π (cm/s)$
-
D.
$5 (cm/s)$
Vật dao động điều hòa với phương trình $x = 4cos(10πt + π/3) cm$. Vào lúc $t = 0,5s$ thì vật có li độ và vận tốc là:
-
A.
$x = - 2cm;{\text{ }}v = - 10\pi \sqrt 3 cm/s$
-
B.
$x{\text{ }} = {\text{ }}2cm;v = 20\pi \sqrt 3 cm/s$
-
C.
$x = 2cm;{\text{ }}v = - 20\pi \sqrt 3 cm/s$
-
D.
$x = - 2cm;{\text{ }}v = 20\pi \sqrt 3 cm/s$
Một chất điểm dao động điều hòa theo phương trình \(x = 5cos(2\pi t + \pi ){\text{ }}\left( {cm} \right)\). Quãng đường vật đi được sau $2s$ là
-
A.
20 cm
-
B.
10cm
-
C.
40 cm
-
D.
80cm
Một vật dao động điều hòa có phương trình: \(x = 5cos(2\pi t + \pi /6){\rm{ }}\left( {cm,{\rm{ }}s} \right)\) . Lấy \(\pi = 3,14\) . Tốc độ của vật khi có li độ \(x = 3cm\) là :
-
A.
$50,24(cm/s)$
-
B.
$2,512(cm/s)$
-
C.
$25,12(cm/s)$
-
D.
$12,56(cm/s)$
Đối với dao động điều hòa, số lần dao động được lặp lại trong một đơn vị thời gian gọi là:
-
A.
Tần số dao động
-
B.
Chu kỳ dao động
-
C.
Pha ban đầu
-
D.
Tần số góc
Trong dao động điều hòa
-
A.
Vận tốc biến đổi điều hoà cùng pha so với li độ
-
B.
Vận tốc biến đổi điều hoà ngược pha so với li độ
-
C.
Vận tốc biến đổi điều hoà sớm pha $π/2$ so với li độ
-
D.
Vận tốc biến đổi điều hoà chậm pha $π/2$ so với li độ
Trong dao động điều hoà
-
A.
Gia tốc biến đổi điều hoà cùng pha so với li độ.
-
B.
Gia tốc biến đổi điều hoà ngược pha so với li độ
-
C.
Gia tốc biến đổi điều hoà sớm pha $π/2$ so với li độ
-
D.
Gia tốc biến đổi điều hoà chậm pha $π/2$ so với li độ
Trong dao động điều hoà
-
A.
Gia tốc biến đổi điều hoà cùng pha so với vận tốc
-
B.
Gia tốc biến đổi điều hoà ngược pha so với vận tốc
-
C.
Gia tốc biến đổi điều hoà sớm pha $π/2$ so với vận tốc
-
D.
Gia tốc biến đổi điều hoà chậm pha $π/2$ so với vận tốc
Chọn câu đúng? Gia tốc trong dao động điều hòa
-
A.
Luôn hướng về vị trí biên.
-
B.
Luôn cùng pha với li độ
-
C.
Độ lớn giá trị nhỏ nhất khi li độ bằng 0
-
D.
Chậm pha \(\frac{\pi }{2}\) so với vận tốc
Một vật đang dao động điều hoà, khi vật chuyển động từ vị trí biên về vị trí cân bằng thì
-
A.
Vật chuyển động nhanh dần đều
-
B.
Vật chuyển động chậm dần đều
-
C.
Gia tốc cùng hướng với chuyển động
-
D.
Gia tốc có độ lớn tăng dần
Khi một vật dao động điều hòa, chuyển động của vật từ vị trí biên về vị trí cân bằng là chuyển động:
-
A.
Nhanh dần đều
-
B.
Chậm dần đều
-
C.
Nhanh dần
-
D.
Chậm dần
Khi nói về dao động điều hoà của một vật, phát biểu nào sau đây sai?
-
A.
Vecto vận tốc và vecto gia tốc của vật luôn ngược chiều nhau
-
B.
Chuyển động của vật từ vị trí cân bằng ra vị trí biên là chuyển động chậm dần
-
C.
Gia tốc luôn hướng về vị trí cân bằng
-
D.
Vecto gia tốc của vật luôn hướng về vị trí cân bằng và có độ lớn tỉ lệ với độ lớn của li độ
Tại thời điểm t thì tích của li độ và vận tốc của vật dao động điều hòa âm (x.v < 0), khi đó
-
A.
Vật đang chuyển động nhanh dần đều theo chiều dương
-
B.
Vật đang chuyển động nhanh dần về vị trí cân bằng
-
C.
Vật đang chuyển động chậm dần theo chiều âm
-
D.
Vật đang chuyển động chậm dần về biên
Đối với dao động cơ điều hòa, chu kì dao động là quãng thời gian ngắn nhất để một trạng thái của dao động lặp lại như cũ. Trạng thái cũ ở đây bao gồm những thông số nào?
-
A.
Vị trí cũ
-
B.
Vận tốc cũ và gia tốc cũ
-
C.
Gia tốc cũ và vị trí cũ
-
D.
Vị trí cũ và vận tốc cũ
Đồ thị biểu diễn mối quan hệ giữa li độ và thời gian là một:
-
A.
Đường thẳng dốc xuống
-
B.
Đường thẳng dốc lên
-
C.
Đường elip
-
D.
Đường hình sin
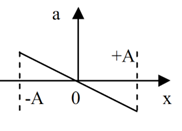
Đồ thị nào sau đây thể hiện đúng sự biến thiên của gia tốc a theo li độ x của một vật dao động điều hoà với biên độ (A)
-
A.
-
B.
-
C.
-
D.
Chọn phát biểu đúng nhất? Hình chiếu của một chuyển động tròn đều lên một đường kính:
-
A.
Là một dao động duy trì
-
B.
Được xem là một dao động điều hòa
-
C.
Là một dao động tuần hoàn
-
D.
Không được xem là một dao động điều hòa
Chọn phát biểu sai về quan hệ giữa chuyển động tròn đều và dao động điều hoà là hình chiếu của nó.
-
A.
Biên độ của dao động bằng bán kính quỹ đạo của chuyển động tròn đều
-
B.
Vận tốc của dao động bằng vận tốc dài của chuyển động tròn đều
-
C.
Tần số góc của dao động bằng tốc độ góc của chuyển động tròn đều
-
D.
Li độ của dao động bằng toạ độ hình chiếu của chuyển động tròn đều
Vật có đồ thị li độ dao động như hình vẽ. Biên độ và chu kì của vật là:
-
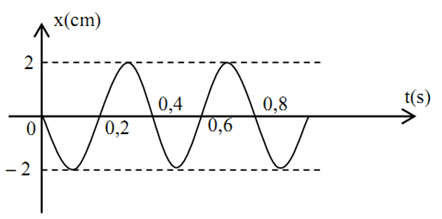
A.
$A=2cm, T=0,8s$
-
B.
$A=4cm, T=0,4s$
-
C.
$A=2cm, T=0,4s$
-
D.
$A=4cm, T=0,8s$
Vật có đồ thị dao động như hình vẽ. Vận tốc cực đại có giá trị
-
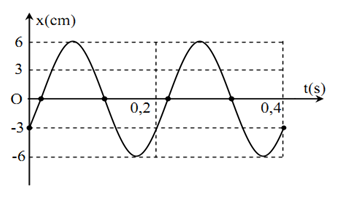
A.
${v_{{\text{max}}}} = 30\pi cm/s$
-
B.
${v_{{\text{max}}}} = 60\pi {\text{cm/s}}$
-
C.
${v_{{\text{max}}}} = 60{\text{cm/s}}$
-
D.
${v_{{\text{max}}}} = 30{\text{cm/s}}$
Vật dao động điều hòa có đồ thị vận tốc - thời gian như hình vẽ. Tần số góc và pha ban đầu của li độ của vật là:
-
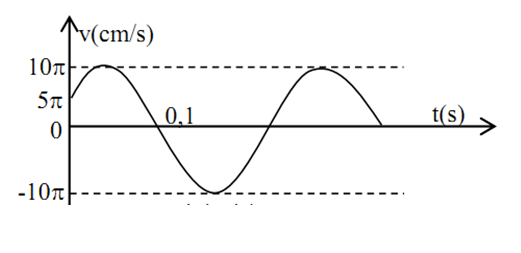
A.
\(\omega = \dfrac{{25\pi }}{3}{\text{,}}\varphi {\text{ = - }}\dfrac{{\pi }}{6}\)
-
B.
\(\omega = \dfrac{{25\pi }}{3}{\text{,}}\varphi {\text{ = }}\dfrac{7\pi }{6}\)
-
C.
\(\omega = \dfrac{{{\text{10}}\pi }}{3}{\text{,}}\varphi {\text{ = }}\dfrac{\pi }{3}\)
-
D.
\(\omega = \dfrac{{{\text{10}}\pi }}{3}{\text{,}}\varphi {\text{ = }}\dfrac{\pi }{2}\)
Vật dao động điều hòa hàm cosin có gia tốc biểu diễn như hình. Biên độ và pha ban đầu của vật là:
-
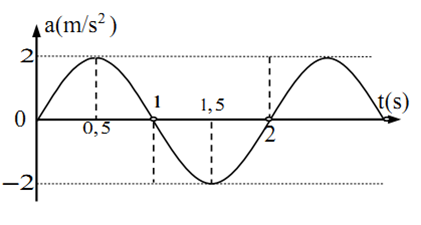
A.
$A = 10cm,\varphi = \frac{\pi }{3}$
-
B.
$A = 20cm,\varphi = {\text{ - }}\frac{\pi }{2}$
-
C.
$A = 20cm,\varphi = 0$
-
D.
$A = 20cm,\varphi = \frac{\pi }{2}$
Một vật dao động điều hòa với phương trình $x = Acos\left( {\omega t + \varphi } \right)$. \(\varphi \) được gọi là:
-
A.
Li độ dao động của vật
-
B.
Pha ban đầu của dao động
-
C.
Biên độ dao động của vật
-
D.
Pha dao động tại thời điểm t
Lời giải và đáp án
Dao động điều hòa là:
-
A.
Dao động trong đó li độ của vật là một hàm tan (hay cotan) của thời gian.
-
B.
Dao động mà vật chuyển động qua lại quanh một vị trí đặc biệt gọi là vị trí cân bằng.
-
C.
Dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.
-
D.
Dao động mà trạng thái của vật được lặp lại như cũ, theo hướng cũ sau những khoảng thời gian bằng nhau xác định.
Đáp án : C
Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.
Một chất điểm dao động điều hòa với phương trình $x = Ac{\rm{os(}}\omega {\rm{t + }}\varphi {\rm{)}}$, trong đó ω có giá trị dương. Đại lượng ω gọi là
-
A.
Biên độ dao động.
-
B.
Chu kì của dao động.
-
C.
Tần số góc của dao động.
-
D.
Pha ban đầu của dao động.
Đáp án : C
ω: tần số góc của dao động (đơn vị: rad/s)
Một chất điểm dao động điều hòa với phương trình $x =Acos(ωt + φ)$; trong đó $A, ω$ là các hằng số dương. Pha của dao động ở thời điểm $t$ là
-
A.
$(\omega t + \varphi )$
-
B.
$ω$
-
C.
$φ$
-
D.
$ωt$
Đáp án : A
$x = Ac{\text{os(}}\omega {\text{t + }}\varphi {\text{)}}$
$ωt+φ$: pha của dao động tại thời điểm $t$ (đơn vị: rad)
Trong dao động điều hòa của một vật thì tập hợp 2 đại lượng nào sau đây là không đổi theo thời gian?
-
A.
Biên độ, tần số.
-
B.
Biên độ, gia tốc.
-
C.
Vận tốc, tần số.
-
D.
Li độ, vận tốc.
Đáp án : A
$x = Ac{\text{os(}}\omega {\text{t + }}\varphi {\text{)}}$
$A$: biên độ dao động
Tần số $f$: Là số dao động toàn phần thực hiện được trong một giây.
Vận tốc: $v = x' = - \omega A\sin (\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \frac{\pi }{2})$
Gia tốc: $a = v' = - {\omega ^2}A\cos (\omega t + \varphi ) = - {\omega ^2}x = {\omega ^2}A\cos (\omega t + \varphi + \pi )$
Ta nhận thấy li độ $x$, vận tốc, gia tốc luôn biến đổi
$A, f$ không đổi
Pha của dao động được dùng để xác định
-
A.
Biên độ dao động
-
B.
Trạng thái dao động
-
C.
Tần số dao động
-
D.
Chu kỳ dao động
Đáp án : B
\(\left( {\omega t + \varphi } \right)\) - Pha của dao động cho biết trạng thái dao động (gồm li độ \(x\) và chiều chuyển động \(\overrightarrow v \) )
Pha ban đầu của dao động điều hòa phụ thuộc
-
A.
Cách chọn gốc tọa độ và gốc thời gian
-
B.
Năng lượng truyền cho vật để vật dao động
-
C.
Đặc tính của hệ dao động
-
D.
Cách kích thích vật dao động
Đáp án : A
Pha ban đầu là pha của dao động tại $t=0$
=> Pha ban đầu của dao động điều hòa phụ thuộc vào cách chọn gốc tọa độ và gốc thời gian
Biên độ dao động:
-
A.
Là quãng đường vật đi trong một chu kỳ dao động
-
B.
Là quãng đường vật đi được trong nửa chu kỳ dao động
-
C.
Là độ dời lớn nhất của vật trong quá trình dao động
-
D.
Là độ dài quỹ đạo chuyển động của vật
Đáp án : C
Ta có:
Quãng đường vật đi trong một chu kỳ dao động là $4A$
Quãng đường vật đi được trong nửa chu kỳ dao động là $2A$
Độ dời lớn nhất của vật trong quá trình dao động là $A$
Độ dài quỹ đạo chuyển động của vật là $2A$
Một vật dao động điều hoà dọc theo trục Ox với phương trình: \(x{\text{ }} = {\text{ }}Acos(\pi t){\text{ }}cm\). Nếu chọn gốc toạ độ O tại vị trí cân bằng của vật thì gốc thời gian $t = 0$ là lúc vật:
-
A.
Ở vị trí li độ cực đại thuộc phần dương của trục Ox
-
B.
Qua vị trí cân bằng O ngược chiều dương của trục Ox
-
C.
Ở vị trí li độ cực đại thuộc phần âm của trục Ox
-
D.
Qua vị trí cân bằng O theo chiều dương của trục Ox
Đáp án : A
Phương trình dao động của vật: \(x = Acos\left( {\pi t} \right)\)
Tại thời điểm ban đầu \(t = 0\), ta có: \(x = Acos\left( {\pi .0} \right) = Acos0 = A\)
=> Lúc \(t = 0\) vật ở vị trí li độ cực đại thuộc phần dương của trục Ox
Một vật dao động điều hòa theo phương trình li độ $x = 5cosπt (cm)$. Tốc độ cực đại của vật bằng:
-
A.
$π (cm/s)$
-
B.
$5/π (cm/s)$
-
C.
$5π (cm/s)$
-
D.
$5 (cm/s)$
Đáp án : C
Sử dụng công thức xác định vận tốc cực đại: ${v_{{\text{max}}}} = A\omega $
Ta có: ${v_{{\text{max}}}} = A\omega = 5.\pi = 5\pi {\text{ }}cm/s$
Vật dao động điều hòa với phương trình $x = 4cos(10πt + π/3) cm$. Vào lúc $t = 0,5s$ thì vật có li độ và vận tốc là:
-
A.
$x = - 2cm;{\text{ }}v = - 10\pi \sqrt 3 cm/s$
-
B.
$x{\text{ }} = {\text{ }}2cm;v = 20\pi \sqrt 3 cm/s$
-
C.
$x = 2cm;{\text{ }}v = - 20\pi \sqrt 3 cm/s$
-
D.
$x = - 2cm;{\text{ }}v = 20\pi \sqrt 3 cm/s$
Đáp án : D
Ta có:
$\begin{gathered}x = 4c{\text{os(10}}\pi {\text{t + }}\frac{\pi }{3}) \hfill \\v = - 40\pi \sin (10\pi t + \frac{\pi }{3}) \hfill \\\end{gathered} $
Tại $t=0,5s$ thay vào phương trình trên $ \to x = - 2cm,{\text{ v = 20}}\pi \sqrt 3 {\text{ cm/s}}$
Một chất điểm dao động điều hòa theo phương trình \(x = 5cos(2\pi t + \pi ){\text{ }}\left( {cm} \right)\). Quãng đường vật đi được sau $2s$ là
-
A.
20 cm
-
B.
10cm
-
C.
40 cm
-
D.
80cm
Đáp án : C
+ Áp dụng biểu thức tính chu kì: \(T = \dfrac{{2\pi }}{\omega }\)
+ Vận dụng công thức quãng đường đi được của vật trong 1 chu kì: \(S = 4A\)
Ta có:
+ Chu kì dao động của vật: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1{\rm{s}}\)
\(\Delta t = 2s = 2T\)
+ Trong 1 chu kì vật đi được quãng đường \(4A\)
=> Quãng đường vật đi được sau \(2s\) là: \(2.4A = 40{\rm{ }}cm\)
Một vật dao động điều hòa có phương trình: \(x = 5cos(2\pi t + \pi /6){\rm{ }}\left( {cm,{\rm{ }}s} \right)\) . Lấy \(\pi = 3,14\) . Tốc độ của vật khi có li độ \(x = 3cm\) là :
-
A.
$50,24(cm/s)$
-
B.
$2,512(cm/s)$
-
C.
$25,12(cm/s)$
-
D.
$12,56(cm/s)$
Đáp án : C
Vận dụng hệ thức độc lập theo thời gian x-v-A: ${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}$
Tại li độ $x=3cm$, ta có:
${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \leftrightarrow {5^2} = {3^2} + \dfrac{{{v^2}}}{{{{\left( {2\pi } \right)}^2}}} \to v = 8\pi = 25,12cm/s$
Đối với dao động điều hòa, số lần dao động được lặp lại trong một đơn vị thời gian gọi là:
-
A.
Tần số dao động
-
B.
Chu kỳ dao động
-
C.
Pha ban đầu
-
D.
Tần số góc
Đáp án : A
Chu kì T: Là khoảng thời gian để vật thực hiện được một dao động toàn phần.
Tần số: số dao động vật thực hiện được trong 1s
Trong dao động điều hòa
-
A.
Vận tốc biến đổi điều hoà cùng pha so với li độ
-
B.
Vận tốc biến đổi điều hoà ngược pha so với li độ
-
C.
Vận tốc biến đổi điều hoà sớm pha $π/2$ so với li độ
-
D.
Vận tốc biến đổi điều hoà chậm pha $π/2$ so với li độ
Đáp án : C
Ta có: .
$\begin{gathered}x = Acos(\omega t + \varphi ) \hfill \\v = x' = - \omega A\sin (\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \frac{\pi }{2}) \hfill \\\end{gathered} $
Trong dao động điều hoà
-
A.
Gia tốc biến đổi điều hoà cùng pha so với li độ.
-
B.
Gia tốc biến đổi điều hoà ngược pha so với li độ
-
C.
Gia tốc biến đổi điều hoà sớm pha $π/2$ so với li độ
-
D.
Gia tốc biến đổi điều hoà chậm pha $π/2$ so với li độ
Đáp án : B
Ta có:
$\begin{gathered}x = A\cos (\omega t + \varphi ) \hfill \\a = v' = - {\omega ^2}A\cos (\omega t + \varphi ) = - {\omega ^2}x ={\omega ^2}A\cos (\omega t + \varphi + \pi ) \hfill \\\end{gathered} $
Trong dao động điều hoà
-
A.
Gia tốc biến đổi điều hoà cùng pha so với vận tốc
-
B.
Gia tốc biến đổi điều hoà ngược pha so với vận tốc
-
C.
Gia tốc biến đổi điều hoà sớm pha $π/2$ so với vận tốc
-
D.
Gia tốc biến đổi điều hoà chậm pha $π/2$ so với vận tốc
Đáp án : C
$\begin{gathered}x = Acos(\omega t + \varphi ) \hfill \\v = x' = - \omega A\sin (\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \frac{\pi }{2}) \hfill \\a = v' = - {\omega ^2}A\cos (\omega t + \varphi ) = - {\omega ^2}x = {\omega ^2}A\cos (\omega t + \varphi + \pi ) \hfill \\\end{gathered} $
Chọn câu đúng? Gia tốc trong dao động điều hòa
-
A.
Luôn hướng về vị trí biên.
-
B.
Luôn cùng pha với li độ
-
C.
Độ lớn giá trị nhỏ nhất khi li độ bằng 0
-
D.
Chậm pha \(\frac{\pi }{2}\) so với vận tốc
Đáp án : C
Ta có:
$\begin{gathered}x = Acos(\omega t + \varphi ) \hfill \\v = x' = - \omega A\sin (\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \frac{\pi }{2}) \hfill \\a = v' = - {\omega ^2}A\cos (\omega t + \varphi ) = - {\omega ^2}x = {\omega ^2}A\cos (\omega t + \varphi + \pi ) \hfill \\\end{gathered} $
Mặt khác: gia tốc $a$ luôn hướng về vị trí cân bằng
Gia tốc: $a = - {\omega ^2}x$
$x=0=>a=0$
Một vật đang dao động điều hoà, khi vật chuyển động từ vị trí biên về vị trí cân bằng thì
-
A.
Vật chuyển động nhanh dần đều
-
B.
Vật chuyển động chậm dần đều
-
C.
Gia tốc cùng hướng với chuyển động
-
D.
Gia tốc có độ lớn tăng dần
Đáp án : C
Khi vật chuyển động từ vị trí biên về vị trí cân bằng, ta có:
+ vận tốc tăng
+ li độ giảm
=> Vật chuyển động nhanh dần, gia tốc có độ lớn giảm dần
Mặt khác: gia tốc luôn hướng về vị trí cân bằng
Khi một vật dao động điều hòa, chuyển động của vật từ vị trí biên về vị trí cân bằng là chuyển động:
-
A.
Nhanh dần đều
-
B.
Chậm dần đều
-
C.
Nhanh dần
-
D.
Chậm dần
Đáp án : C
Khi vật từ vị trí biên về vị trí cân bằng:
+ vận tốc tăng
+ li độ giảm
=> Vật chuyển động nhanh dần
Khi nói về dao động điều hoà của một vật, phát biểu nào sau đây sai?
-
A.
Vecto vận tốc và vecto gia tốc của vật luôn ngược chiều nhau
-
B.
Chuyển động của vật từ vị trí cân bằng ra vị trí biên là chuyển động chậm dần
-
C.
Gia tốc luôn hướng về vị trí cân bằng
-
D.
Vecto gia tốc của vật luôn hướng về vị trí cân bằng và có độ lớn tỉ lệ với độ lớn của li độ
Đáp án : A
Ta có: gia tốc a
+ Gia tốc luôn hướng về vị trí cân bằng
+ a=-ω2x
Vận tốc: trong 1 chu kì đổi chiều 2 lần
Tại thời điểm t thì tích của li độ và vận tốc của vật dao động điều hòa âm (x.v < 0), khi đó
-
A.
Vật đang chuyển động nhanh dần đều theo chiều dương
-
B.
Vật đang chuyển động nhanh dần về vị trí cân bằng
-
C.
Vật đang chuyển động chậm dần theo chiều âm
-
D.
Vật đang chuyển động chậm dần về biên
Đáp án : B
Ta có: x.v < 0, có thể xảy ra 2 TH
+ x > 0,v < 0 : Vật đi từ A => 0: Vật đang chuyển động danh dần theo chiều âm
+ x < 0, v > 0: Vật đi từ -A=> 0: Vật đang chuyển động nhanh dần theo chiều dương
=> x.v <0: Vật đang chuyển động nhanh dần về vị trí cân bằng
Đối với dao động cơ điều hòa, chu kì dao động là quãng thời gian ngắn nhất để một trạng thái của dao động lặp lại như cũ. Trạng thái cũ ở đây bao gồm những thông số nào?
-
A.
Vị trí cũ
-
B.
Vận tốc cũ và gia tốc cũ
-
C.
Gia tốc cũ và vị trí cũ
-
D.
Vị trí cũ và vận tốc cũ
Đáp án : D
Trạng thái của dao động bao gồm vị trí cũ và vận tốc cũ
Đồ thị biểu diễn mối quan hệ giữa li độ và thời gian là một:
-
A.
Đường thẳng dốc xuống
-
B.
Đường thẳng dốc lên
-
C.
Đường elip
-
D.
Đường hình sin
Đáp án : D
Đồ thị của dao động điều hòa là một đường hình sin
=> Chọn D
Đồ thị nào sau đây thể hiện đúng sự biến thiên của gia tốc a theo li độ x của một vật dao động điều hoà với biên độ (A)
-
A.
-
B.
-
C.
-
D.
Đáp án : D
Sử dụng phương trình gia tốc của vật dao động điều hòa: $a = - {\omega ^2}x$
Ta có: $a = - {\omega ^2}x$
=> (có dạng đồ thị của hàm số y=ax) Đồ thị (a-x) là đoạn thẳng đi qua gốc tọa độ.
Chọn phát biểu đúng nhất? Hình chiếu của một chuyển động tròn đều lên một đường kính:
-
A.
Là một dao động duy trì
-
B.
Được xem là một dao động điều hòa
-
C.
Là một dao động tuần hoàn
-
D.
Không được xem là một dao động điều hòa
Đáp án : B
Hình chiếu của một chuyển động tròn đều lên một đường kính được xem là một dao động điều hòa
Chọn phát biểu sai về quan hệ giữa chuyển động tròn đều và dao động điều hoà là hình chiếu của nó.
-
A.
Biên độ của dao động bằng bán kính quỹ đạo của chuyển động tròn đều
-
B.
Vận tốc của dao động bằng vận tốc dài của chuyển động tròn đều
-
C.
Tần số góc của dao động bằng tốc độ góc của chuyển động tròn đều
-
D.
Li độ của dao động bằng toạ độ hình chiếu của chuyển động tròn đều
Đáp án : B
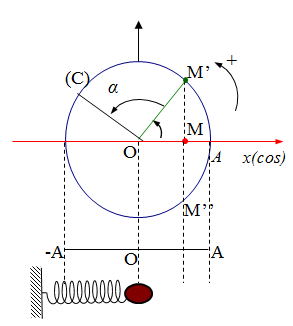
DĐĐH được xem là hình chiếu của một chất điểm chuyển động tròn đều lên một trục nằm trong mặt phẳng quỹ đạo. Với: \(A = R;\omega = \frac{v}{R}\)
Vật có đồ thị li độ dao động như hình vẽ. Biên độ và chu kì của vật là:
-
A.
$A=2cm, T=0,8s$
-
B.
$A=4cm, T=0,4s$
-
C.
$A=2cm, T=0,4s$
-
D.
$A=4cm, T=0,8s$
Đáp án : C
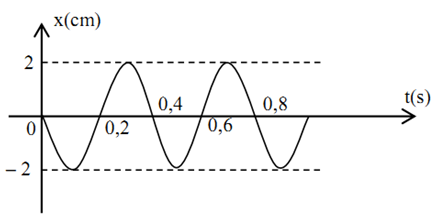
Từ đồ thị, ta có:
$\begin{gathered}A = 2cm \hfill \\T = 0,4{\text{s}} \hfill \\\end{gathered} $
Vật có đồ thị dao động như hình vẽ. Vận tốc cực đại có giá trị
-
A.
${v_{{\text{max}}}} = 30\pi cm/s$
-
B.
${v_{{\text{max}}}} = 60\pi {\text{cm/s}}$
-
C.
${v_{{\text{max}}}} = 60{\text{cm/s}}$
-
D.
${v_{{\text{max}}}} = 30{\text{cm/s}}$
Đáp án : B
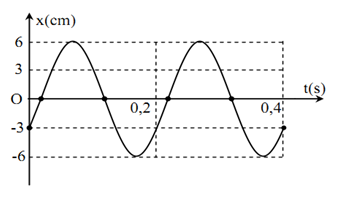
Ta có:
$\begin{gathered}A = 6cm \hfill \\2T = 0,4{\text{s}} \to T = 0,2{\text{s}} \to \omega {\text{ = }}\frac{{2\pi }}{T} = 10\pi ra{\text{d}}/s \hfill \\\end{gathered} $
$ \to {v_{{\text{max}}}} = A\omega = 60\pi cm/s$
Vật dao động điều hòa có đồ thị vận tốc - thời gian như hình vẽ. Tần số góc và pha ban đầu của li độ của vật là:
-
A.
\(\omega = \dfrac{{25\pi }}{3}{\text{,}}\varphi {\text{ = - }}\dfrac{{\pi }}{6}\)
-
B.
\(\omega = \dfrac{{25\pi }}{3}{\text{,}}\varphi {\text{ = }}\dfrac{7\pi }{6}\)
-
C.
\(\omega = \dfrac{{{\text{10}}\pi }}{3}{\text{,}}\varphi {\text{ = }}\dfrac{\pi }{3}\)
-
D.
\(\omega = \dfrac{{{\text{10}}\pi }}{3}{\text{,}}\varphi {\text{ = }}\dfrac{\pi }{2}\)
Đáp án : B
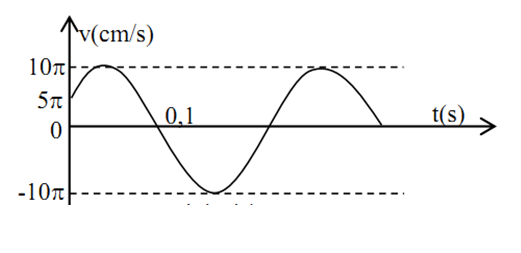
Ta có:
$\left\{ \begin{gathered}A\omega = 10\pi cm/s \hfill \\\dfrac{{5T}}{{12}} = 0,1{\text{s}} \to T = 0,24{\text{s}} \to \omega = \dfrac{{25\pi }}{3}ra{\text{d}}/s \hfill \\\end{gathered} \right.$
Tại \(t = 0\): \(\left\{ \begin{array}{l}v = 5\pi \\v > 0\end{array} \right. \leftrightarrow \left\{ \begin{array}{l} - A\omega \sin \varphi {\rm{ = 5}}\pi \\{\rm{sin}}\varphi < 0\end{array} \right. \leftrightarrow \left\{ \begin{array}{l}\sin \varphi {\rm{ = }}\dfrac{{{\rm{ - 5}}\pi }}{{10\pi }} = \dfrac{{{\rm{ - 1}}}}{2}\\{\rm{sin}}\varphi < 0\end{array} \right. \to \varphi = \left[ \begin{array}{l} - \dfrac{\pi }{6}\\\dfrac{{7\pi }}{6}\end{array} \right.\)
Mặt khác, vận tốc đang tăng => \(\varphi = \dfrac{{7\pi }}{6}\)
Vật dao động điều hòa hàm cosin có gia tốc biểu diễn như hình. Biên độ và pha ban đầu của vật là:
-
A.
$A = 10cm,\varphi = \frac{\pi }{3}$
-
B.
$A = 20cm,\varphi = {\text{ - }}\frac{\pi }{2}$
-
C.
$A = 20cm,\varphi = 0$
-
D.
$A = 20cm,\varphi = \frac{\pi }{2}$
Đáp án : D
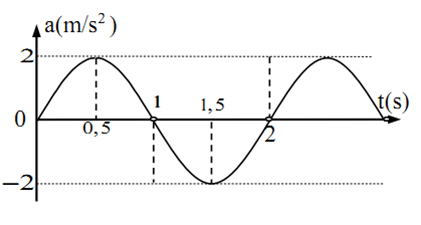
Ta có:
$\left\{ \begin{gathered}A{\omega ^2} = 2m/{s^2} \hfill \\T = 2{\text{s}} \to \omega = \pi ra{\text{d}}/s \hfill \\\end{gathered} \right. \to A = \frac{2}{{{\pi ^2}}} = 0,2m = 20cm$
Tại t=0: a=0 và đang đi lên => x=0 và đi theo chiều âm.
$\to \left\{ \begin{gathered}x = 0 \hfill \\v < 0 \hfill \\\end{gathered} \right. \leftrightarrow \left\{ \begin{gathered}Ac{\text{os}}\varphi {\text{ = 0}} \hfill \\{\text{sin}}\varphi > 0 \hfill \\\end{gathered} \right. \leftrightarrow \left\{ \begin{gathered}c{\text{os}}\varphi {\text{ = 0}} \hfill \\{\text{sin}}\varphi > 0 \hfill \\\end{gathered} \right. \to \varphi = \frac{\pi }{2}$
$ \to A = 20cm,\varphi = \frac{\pi }{2}$
Một vật dao động điều hòa với phương trình $x = Acos\left( {\omega t + \varphi } \right)$. \(\varphi \) được gọi là:
-
A.
Li độ dao động của vật
-
B.
Pha ban đầu của dao động
-
C.
Biên độ dao động của vật
-
D.
Pha dao động tại thời điểm t
Đáp án : B
Ta có: \(x = Acos\left( {\omega t + \varphi } \right)\)
+ \(x\): li độ dao động của vật
+ \(A\): Biên độ dao động của vật
+ \(\omega \): Tần số góc của dao động
+ \(\varphi \): Pha ban đầu của dao động
+ \(\omega t + \varphi \): Pha dao động tại thời điểm t
Luyện tập và củng cố kiến thức Bài 1. Dao động điều hòa - Các đại lượng đặc trưng Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1. Viết phương trình dao động điều hòa Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1. Ứng dụng vòng tròn lượng giác Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1. Bài tập quãng đường, tốc độ trung bình Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2. Con lắc lò xo - Bài tập chu kì, tần số, tần số góc của con lắc lò xo Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2. Năng lượng của con lắc lò xo Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2. Chiều dài con lắc lò xo Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2. Thời gian nén - giãn của con lắc lò xo Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2. Va chạm con lắc lò xo Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3. Con lắc đơn - Các đại lượng đặc trưng Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3. Năng lượng, vận tốc - lực của con lắc đơn Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4. Sự thay đổi chu kì con lắc đơn khi chịu thêm tác dụng của lực lạ Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4. Sự nhanh chậm của đồng hồ quả lắc Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4. Con lắc vướng đinh - sự trùng phùng của hai con lắc Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập các loại dao động Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập dao động điều hòa Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập dao động cơ (phần 1) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập dao động cơ (phần 2) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập dao động cơ (phần 3) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập chương 1 Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
