Trắc nghiệm Tổng hợp bài tập về phóng xạ - Vật Lí 12
Đề bài
Trong các biểu thức sau đây, biểu thức nào đúng với nội dung của định luật phóng xạ? (với m0 là khối lượng của chất phóng xạ ban đầu, m là khối lượng chất phóng xạ còn lại tại thời điểm t, $\lambda $ là hằng số phóng xạ).
-
A.
\(m{}_0 = m.{e^{ - \lambda t}}\)
-
B.
\(m = {m_0}.{e^{ - \lambda t}}\)
-
C.
\(m = m{._0}{e^{\lambda t}}\)
-
D.
\(m = \frac{1}{2}{m_0}.{e^{ - \lambda t}}\)
Biểu thức xác định số hạt nhân còn lại sau thời gian t là:
-
A.
\(N = {N_0}{.2^{{\kern 1pt} \frac{t}{T}}}\)
-
B.
\(N = \frac{{{N_0}}}{{{e^{ - \lambda .t}}}}\)
-
C.
\(N = \frac{{{N_0}}}{{{2^{\frac{t}{T}}}}}\)
-
D.
\(N = {N_0}.{e^{\lambda .t}}\)
Biểu thức xác định độ phóng xạ của một chất sau thời gian t là:
-
A.
\(H = {H_0}{.2^{\lambda t}}\)
-
B.
\(H = \frac{{{H_0}}}{{{e^{\lambda t}}}}\)
-
C.
\(H = {H_0}{.2^{ - \lambda t}}\)
-
D.
\(H = \frac{{{H_0}}}{{{2^{ - \frac{t}{T}}}}}\)
Chất Iốt phóng xạ \({}_{53}^{131}\)I dùng trong y tế có chu kỳ bán rã 8 ngày đêm. Nếu nhận được 100g chất này thì sau 8 tuần lễ còn bao nhiêu?
-
A.
0,87g
-
B.
0,78g
-
C.
7,8g
-
D.
8,7g
Một chất phóng xạ ban đầu có N0 hạt nhân. Sau 1 năm, còn lại một phần ba số hạt nhân ban đầu chưa phân rã. Sau 1 năm nữa, số hạt nhân còn lại chưa phân rã của chất phóng xạ đó là:
-
A.
N0/6
-
B.
N0 /16
-
C.
N0/9
-
D.
N0 /4
Một chất phóng xạ có chu kỳ bán rã là 3,8 ngày. Sau thời gian 11,4 ngày thì độ phóng xạ (hoạt độ phóng xạ) của lượng chất phóng xạ còn lại bằng bao nhiêu phần trăm so với độ phóng xạ của lượng chất phóng xạ ban đầu?
-
A.
25%
-
B.
75%
-
C.
12,5%
-
D.
87,5%
Biểu thức xác định khối lượng hạt nhân đã phân rã trong thời gian t là:
-
A.
\(\Delta m{\rm{ }} = {m_0}(1 - {2^{ - \frac{t}{T}}})\)
-
B.
\(\Delta m{\rm{ }} = {m_0}{2^{ - \frac{t}{T}}}\)
-
C.
\(\Delta m{\rm{ = }}{m_0}(1 - {e^{\lambda .t}})\)
-
D.
\(\Delta m{\rm{ }} = {m_0}{e^{\lambda .t}}\)
Số hạt nhân đã bị phân rã được xác định bằng biểu thức nào dưới đây?
-
A.
\(\Delta N = {N_0}(1 - {2^{ - \frac{t}{T}}})\)
-
B.
\(\Delta N{\rm{ }} = {N_0}{2^{ - \frac{t}{T}}}\)
-
C.
\(\Delta N{\rm{ }} = {N_0}(1 - {e^{\lambda .t}})\)
-
D.
\(\Delta N{\rm{ }} = {N_0}{e^{ - \lambda .t}}\)
\({}^{22}Na\) phân rã với chu kì T = 2,6 năm. Khối lượng ban đầu là m0. Sau 2 năm lượng \({}^{22}Na\) phân rã bao nhiêu %?
-
A.
41,3%
-
B.
50%
-
C.
25%
-
D.
67,7%
Tính số hạt nhân bị phân rã sau 1s trong 1g Rađi \({}^{226}\)Ra . Cho biết chu kỳ bán rã của \({}^{226}\)Ra là 1580 năm. Số Avôgađrô là NA = 6,02.1023 mol-1.
-
A.
3,55.1010 hạt
-
B.
3,40.1010 hạt
-
C.
3,75.1010 hạt
-
D.
3,70.1010 hạt
Pôlôni \(^{210}Po\) là một chất phóng xạ có chu kì bán rã \(140\) ngày đêm. Hạt nhân pôlôni phóng xạ sẽ biến thành hạt nhân chì (\(^{206}Pb\)) và kèm theo một hạt a. Ban đầu có \(42 mg\) chất phóng xạ pôlôni. Khối lượng chì sinh ra sau \(280\) ngày đêm là:
-
A.
30,9 mg
-
B.
10,35 mg
-
C.
31,96 mg
-
D.
10,65 mg
Đồng vị \({}_{11}^{24}\) Na là chất phóng xạ β- tạo thành hạt nhân magiê( \({}_{12}^{24}\)Mg). Ban đầu có 12gam Na và chu kì bán rã là 15 giờ. Sau 45 h thì khối lượng Mg tạo thành là :
-
A.
10,5 g
-
B.
5,16 g
-
C.
51,6 g
-
D.
0,516 g
Phương trình phóng xạ của Pôlôni có dạng:\({}_{84}^{210}Po\)\( \to {}_Z^APb + \alpha \).Cho chu kỳ bán rã của Pôlôni T=138 ngày. Khối lượng ban đầu m0=1g. Hỏi sau bao lâu khối lượng Pôlôni chỉ còn 0,707g?
-
A.
69 ngày
-
B.
138 ngày
-
C.
97,57 ngày
-
D.
195,19 ngày
Một lượng chất phóng xạ sau 12 năm thì còn lại 1/16 khối lượng ban đầu của nó. Chu kì bán rã của chất đó là
-
A.
3 năm
-
B.
4,5 năm
-
C.
9 năm
-
D.
48 năm
Một đồng vị phóng xạ có chu kì bán rã T. Cứ sau một khoảng thời gian bằng bao nhiêu thì số hạt nhân bị phân rã trong khoảng thời gian đó bằng ba lần số hạt nhân còn lại của đồng vị ấy
-
A.
2T
-
B.
3T
-
C.
0,5T
-
D.
T
\(_{11}^{24}Na\) là chất phóng xạ \({\beta ^ - }\) với chu kỳ bán rã 15 giờ. Ban đầu có một lượng \(_{11}^{24}Na\) thì sau một khoảng thời gian bao nhiêu lượng chất phóng xạ trên bị phân rã 75%?
-
A.
7h30'
-
B.
15h00'
-
C.
22h30'
-
D.
30h00'
Một lượng chất phóng xạ \({}_{86}^{222}Rn\) ban đầu có khối lượng 1mg. Sau 15,2 ngày độ phóng xạ giảm 93,75%. Chu kỳ bán rã của Rn là:
-
A.
4 ngày
-
B.
3,8 ngày
-
C.
3,5 ngày
-
D.
2,7 ngày
Hạt nhân A (có khối lượng mA) đứng yên phóng xạ thành hạt B (có khối lượng mB) và C (có khối lượng mC) theo phương trình \(A \to B + C\). Nếu phản ứng tỏa năng lượng ∆E thì động năng của B là:
-
A.
\(\frac{{{m_B}}}{{{m_C} + {m_B}}}\Delta E\)
-
B.
\(\frac{{{m_C}}}{{{m_C} + {m_B}}}\Delta E\)
-
C.
\(\frac{{\left( {{m_C} + {m_B}} \right)}}{{{m_C}}}\Delta E\)
-
D.
\(\frac{{{m_B}}}{{{m_C}}}\Delta E\)
Hạt nhân \(A\) đang đứng yên thì phân rã thành hạt nhân \(B\) có khối lượng \(m_B\) và hạt $\alpha $ có khối lượng \(m_{\alpha}\). Tỉ số giữa động năng của hạt $\alpha $ và động năng của hạt nhân \(B\) ngay sau phân rã bằng:
-
A.
\({\left( {\dfrac{{{m_\alpha }}}{{{m_B}}}} \right)^2}\)
-
B.
\(\dfrac{{{m_B}}}{{{m_\alpha }}}\)
-
C.
\(\dfrac{{{m_\alpha }}}{{{m_B}}}\)
-
D.
\({\left( {\dfrac{{{m_B}}}{{{m_\alpha }}}} \right)^2}\)
Chất phóng xạ \({}_{84}^{210}Po\) phát ra tia α và biến đổi thành \({}_{82}^{206}Pb\). Biết khối lượng các hạt là mPb = 205,9744u, mPo = 209,9828u, mα = 4,0026u. Giả sử hạt nhân mẹ ban đầu đứng yên và sự phân rã không phát ra tia γ thì động năng của hạt nhân con là
-
A.
0,1MeV
-
B.
0,02MeV
-
C.
0,01MeV
-
D.
0,2MeV
Một hạt nhân X, ban đầu đứng yên, phóng xạ α và biến thành hạt nhân Y. Biết hạt nhân X có số khối là A, hạt α phát ra tốc độ v. Lấy khối lượng của hạt nhân bằng số khối của nó tính theo đơn vị u. Tốc độ của hạt nhân Y bằng:
-
A.
\(\frac{{2v}}{{A - 4}}\)
-
B.
\(\frac{{4v}}{{A + 4}}\)
-
C.
\(\frac{{2v}}{{A + 4}}\)
-
D.
\(\frac{{4v}}{{A - 4}}\)
\(_{92}^{235}U + _0^1n \to _{42}^{95}Mo + _{57}^{139}La + 2_0^1n + 7{e^ - }\) là một phản ứng phân hạch của Urani 235. Biết khối lượng hạt nhân : \({m_U} = {\rm{ }}234,99{\rm{ }}u\) ; \({m_{Mo}} = {\rm{ }}94,88{\rm{ }}u\) ;\({m_{La}} = {\rm{ }}138,87{\rm{ }}u\) ;\({m_n} = {\rm{ }}1,0087{\rm{ }}u\). Cho năng suất toả nhiệt của xăng là \({46.10^6}J/kg\). Khối lượng xăng cần dùng để có thể toả năng lượng tương đương với 1 gam U phân hạch ? Lấy \(1u{c^2} = 931MeV\)
-
A.
1616 kg
-
B.
1717 kg
-
C.
1818 kg
-
D.
1919 kg
Hiện nay trong quặng thiên nhiên có chứa cả \(_{92}^{238}U\) và \(_{92}^{235}U\) theo tỉ lệ nguyên tử là 140 :1. Giả sử ở thời điểm tạo thành Trái Đất, tỷ lệ trên là 1:1. Hãy tính tuổi của Trái Đất. Biết chu kỳ bán rã của \(_{92}^{238}U\) là 4,5.109 năm, \(_{92}^{235}U\) có chu kỳ bán rã 7,13.108 năm.
-
A.
60,4.108năm
-
B.
64.108 năm
-
C.
51,65.108 năm
-
D.
65.108 năm
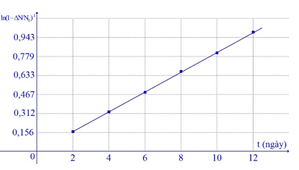
Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã \(T\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \({\rm{\Delta N}}\) và số hạt ban đầu \({{\rm{N}}_{\rm{0}}}{\rm{.}}\) Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này?
-
A.
\(5,6\) ngày
-
B.
\(8,9\) ngày
-
C.
\(3,8\) ngày
-
D.
\(138\) ngày
Hạt nhân Poloni \(\left( {_{84}^{210}Po} \right)\) đứng yên phát ra tia anpha và biến thành hạt nhân chì Pb. Cho \({m_{Po}} = 209,9828u\) , \({m_\alpha } = 4,0026u\), \({m_{Pb}} = 205,9744u\). Tốc độ của hạt nhân chì phóng ra bằng
-
A.
\(30,{6.10^5}m/s\)
-
B.
\({5.10^5}m/s\)
-
C.
\(3,{06.10^5}m/s\)
-
D.
\(3,{06.10^5}cm/s\)
Coban \({}_{27}^{60}Co\) là chất phóng xạ có chu kì bán rã T = 5,33 năm. Lúc đầu có 1000g Co thì sau 10,66 năm số nguyên tử coban còn tại là?
-
A.
\(N = 2,{51.10^{24}}\)
-
B.
\(N = 5,{42.10^{22}}\)
-
C.
\(N = 8,{18.10^{20}}\)
-
D.
\(N = 1,{25.10^{21}}\)
Chất phóng xạ pôlôni \({}_{84}^{210}Po\) có chu kì bán rã 138 ngày. Ban đầu có một mẫu gồm N0 hạt nhân pôlôni \({}_{84}^{210}Po\). Sau bao lâu (kể từ lúc ban đầu), số hạt nhân \({}_{84}^{210}Po\) bị phân rã là \(\dfrac{7}{8}{N_0}\)?
-
A.
276 ngày.
-
B.
414 ngày.
-
C.
552 ngày.
-
D.
690 ngày.
Một chất phóng xạ có chu kì bán rã là 3,8 ngày. Số hạt nhân sẽ bị phân rã hết 70% sau thời gian là
-
A.
6,6 ngày.
-
B.
7,6 ngày.
-
C.
4,8 ngày.
-
D.
8,8 ngày.
Trong điều trị bệnh ung thư, bệnh nhân được chiếu xạ với một liều xác định nào đó từ một nguồn phóng xạ. Biết nguồn có chu kỳ bán rã là 4 năm. Khi nguồn được sử dụng lần đầu thì thời gian cho 1 liều xạ là 10 phút. Hỏi sau hai năm thời gian cho 1 liều xạ là bao nhiêu phút:
-
A.
14
-
B.
10
-
C.
20
-
D.
7
Gọi \({N_0}\) là số hạt nhân phóng xạ ban đầu \(\left( {t = 0} \right)\) và \(\Delta N\) là số hạt nhân đã phóng xạ sau thời gian \(t\). Đồ thị nào sau đây biểu thị sự biến thiên của \(\Delta N\) theo thời gian?

-
A.
Hình A
-
B.
Hình B
-
C.
Hình C
-
D.
Hình D
Các tế bào ung thư dễ bị tổn thương dưới tác dụng của tia X hoặc tia gamma hơn các tế bào khỏe mạnh. Mặc dù ngày nay đã có các máy gia tốc tuyến tính thay thế, nhưng trước kia nguồn tiêu chuẩn để điều trị là phóng xạ \({}^{60}Co\). Đồng vị này phân rã \(\beta \) thành \({}^{60}Ni\) ở trạng thái kích thích, nhưng \({}^{60}Ni\) ngay sau đó trở về trạng thái cơ bản và phát ra hai photon gamma, mỗi photon có năng lượng xấp xỉ 1,2 MeV. Biết rằng chu kì bán rã của phân rã \(\beta \) là 5,27 năm. Xác định số hạt nhân \({}^{60}Co\) có mặt trong nguồn 6000 Ci thường được dùng trong các bệnh viện.
-
A.
\(5,{33.10^{22}}\) hạt.
-
B.
\(3,{2.10^{14}}\) hạt.
-
C.
\(9,{98.10^{11}}\) hạt.
-
D.
\(3,{69.10^{22}}\) hạt.
Lời giải và đáp án
Trong các biểu thức sau đây, biểu thức nào đúng với nội dung của định luật phóng xạ? (với m0 là khối lượng của chất phóng xạ ban đầu, m là khối lượng chất phóng xạ còn lại tại thời điểm t, $\lambda $ là hằng số phóng xạ).
-
A.
\(m{}_0 = m.{e^{ - \lambda t}}\)
-
B.
\(m = {m_0}.{e^{ - \lambda t}}\)
-
C.
\(m = m{._0}{e^{\lambda t}}\)
-
D.
\(m = \frac{1}{2}{m_0}.{e^{ - \lambda t}}\)
Đáp án : B
Xem lại lí thuyết dạng 1
Khối lượng chất phóng xạ còn lại: \(m = \frac{{{m_0}}}{{{2^{\frac{t}{T}}}}} = {m_0}{2^{ - \frac{t}{T}}} = {m_0}.{e^{ - \lambda t}}\)
Biểu thức xác định số hạt nhân còn lại sau thời gian t là:
-
A.
\(N = {N_0}{.2^{{\kern 1pt} \frac{t}{T}}}\)
-
B.
\(N = \frac{{{N_0}}}{{{e^{ - \lambda .t}}}}\)
-
C.
\(N = \frac{{{N_0}}}{{{2^{\frac{t}{T}}}}}\)
-
D.
\(N = {N_0}.{e^{\lambda .t}}\)
Đáp án : C
Số hạt nhân còn lại: \(N = \frac{{{N_0}}}{{{2^{\frac{t}{T}}}}} = {N_0}{2^{ - \frac{t}{T}}} = {N_0}.{e^{ - \lambda t}}\)
Biểu thức xác định độ phóng xạ của một chất sau thời gian t là:
-
A.
\(H = {H_0}{.2^{\lambda t}}\)
-
B.
\(H = \frac{{{H_0}}}{{{e^{\lambda t}}}}\)
-
C.
\(H = {H_0}{.2^{ - \lambda t}}\)
-
D.
\(H = \frac{{{H_0}}}{{{2^{ - \frac{t}{T}}}}}\)
Đáp án : B
Độ phóng xạ: \(H = \frac{{{H_0}}}{{{2^{\frac{t}{T}}}}} = {H_0}{2^{ - \frac{t}{T}}} = {H_0}.{e^{ - \lambda t}}\)
Chất Iốt phóng xạ \({}_{53}^{131}\)I dùng trong y tế có chu kỳ bán rã 8 ngày đêm. Nếu nhận được 100g chất này thì sau 8 tuần lễ còn bao nhiêu?
-
A.
0,87g
-
B.
0,78g
-
C.
7,8g
-
D.
8,7g
Đáp án : B
Sử dụng công thức xác định khối lượng chất phóng xạ còn lại còn lại: \(m = {m_0}{2^{ - \frac{t}{T}}}\)
t = 8 tuần = 56 ngày = 7.T .Suy ra sau thời gian t thì khối lượng chất phóng xạ \({}_{53}^{131}\)I còn lại là :
\(m = {m_0}{.2^{ - \frac{t}{T}}} = {100.2^{ - 7}}\)= 0,78 gam .
Một chất phóng xạ ban đầu có N0 hạt nhân. Sau 1 năm, còn lại một phần ba số hạt nhân ban đầu chưa phân rã. Sau 1 năm nữa, số hạt nhân còn lại chưa phân rã của chất phóng xạ đó là:
-
A.
N0/6
-
B.
N0 /16
-
C.
N0/9
-
D.
N0 /4
Đáp án : C
Sử dụng công thức xác định số hạt nhân còn lại: \(N = {N_0}{2^{ - \frac{t}{T}}}\)
t1 = 1năm thì số hạt nhân chưa phân rã (còn lại ) là N1, theo đề ta có : \[\frac{{{N_1}}}{{{N_0}}} = \frac{1}{{{2^{\frac{t}{T}}}}} = \frac{1}{3}\]
Sau 1năm nữa tức là t2 = 2t1 năm thì số hạt nhân còn lại chưa phân rã là N2, ta có :
\[\frac{{{N_2}}}{{{N_0}}} = \frac{1}{{{2^{\frac{{{t_2}}}{T}}}}} = \frac{1}{{{2^{\frac{{2{t_1}}}{T}}}}}\] \[ \Leftrightarrow \]\[\frac{{{N_2}}}{{{N_0}}} = {\left( {\frac{1}{{{2^{\frac{t}{T}}}}}} \right)^2} = {\left( {\frac{1}{3}} \right)^2} = \frac{1}{9}\]
Một chất phóng xạ có chu kỳ bán rã là 3,8 ngày. Sau thời gian 11,4 ngày thì độ phóng xạ (hoạt độ phóng xạ) của lượng chất phóng xạ còn lại bằng bao nhiêu phần trăm so với độ phóng xạ của lượng chất phóng xạ ban đầu?
-
A.
25%
-
B.
75%
-
C.
12,5%
-
D.
87,5%
Đáp án : C
Sử dụng công thức xác định độ phóng xạ còn lại: \(H = {H_0}{2^{ - \frac{t}{T}}}\)
T = 3,8 ngày ; t = 11,4 = 3T ngày. Do đó ta đưa về hàm mũ để giải nhanh như sau :
\(H = {H_0}{.2^{ - \frac{t}{T}}} \Leftrightarrow \frac{H}{{{H_0}}} = {2^{ - \frac{t}{T}}}\) \(\Leftrightarrow \) \(\frac{H}{{{H_0}}} = {2^{ - 3}} = \frac{1}{8}\) = 12,5%
Biểu thức xác định khối lượng hạt nhân đã phân rã trong thời gian t là:
-
A.
\(\Delta m{\rm{ }} = {m_0}(1 - {2^{ - \frac{t}{T}}})\)
-
B.
\(\Delta m{\rm{ }} = {m_0}{2^{ - \frac{t}{T}}}\)
-
C.
\(\Delta m{\rm{ = }}{m_0}(1 - {e^{\lambda .t}})\)
-
D.
\(\Delta m{\rm{ }} = {m_0}{e^{\lambda .t}}\)
Đáp án : A
Xem lại lí thuyết dạng 2
Khối lượng hạt nhân đã phân rã: \(\Delta m{\rm{ }} = {m_0}(1 - {2^{ - \frac{t}{T}}}) = {m_0}\left( {1 - {e^{ - \lambda t}}} \right)\)
Số hạt nhân đã bị phân rã được xác định bằng biểu thức nào dưới đây?
-
A.
\(\Delta N = {N_0}(1 - {2^{ - \frac{t}{T}}})\)
-
B.
\(\Delta N{\rm{ }} = {N_0}{2^{ - \frac{t}{T}}}\)
-
C.
\(\Delta N{\rm{ }} = {N_0}(1 - {e^{\lambda .t}})\)
-
D.
\(\Delta N{\rm{ }} = {N_0}{e^{ - \lambda .t}}\)
Đáp án : A
Khối lượng hạt nhân đã phân rã: \(\Delta N{\rm{ }} = {N_0}(1 - {2^{ - \frac{t}{T}}}) = {N_0}\left( {1 - {e^{ - \lambda t}}} \right)\)
\({}^{22}Na\) phân rã với chu kì T = 2,6 năm. Khối lượng ban đầu là m0. Sau 2 năm lượng \({}^{22}Na\) phân rã bao nhiêu %?
-
A.
41,3%
-
B.
50%
-
C.
25%
-
D.
67,7%
Đáp án : A
Sử dụng công thức tính khối lượng hạt nhân đã phân rã: \(\Delta m{\rm{ }} = {m_0}(1 - {2^{ - \frac{t}{T}}})\)
t = 2 năm, T = 2,6 năm
Ta có: khối lượng hạt nhân đã phân rã: \(\Delta m{\rm{ }} = {m_0}(1 - {2^{ - \frac{t}{T}}}) \to \frac{{\Delta m}}{{{m_0}}} = 1 - {2^{ - \frac{t}{T}}} = 1 - {2^{ - \frac{2}{{2,6}}}} = 0,4133 = 41,33\% \)
Tính số hạt nhân bị phân rã sau 1s trong 1g Rađi \({}^{226}\)Ra . Cho biết chu kỳ bán rã của \({}^{226}\)Ra là 1580 năm. Số Avôgađrô là NA = 6,02.1023 mol-1.
-
A.
3,55.1010 hạt
-
B.
3,40.1010 hạt
-
C.
3,75.1010 hạt
-
D.
3,70.1010 hạt
Đáp án : D
Sử dụng công thức tính số hạt nhân đã phân rã: \(\Delta N{\rm{ }} = {N_0}(1 - {2^{ - \frac{t}{T}}})\)
- Số hạt trong n mol: N = n.NA
Số hạt nhân nguyên tử có trong 1 gam 226Ra là :
\(N_0=\dfrac{m}{A}.{N_A} = \dfrac{1}{{226}}.6,{022.10^{23}} = 2,{6646.10^{21}}\) hạt
Suy ra số hạt nhân nguyên tử Ra phân rã sau 1 s là :
\(\Delta N = {N_0}(1 - {2^{ - \dfrac{t}{T}}}) = 2,{6646.10^{21}}\left( {1 - {2^{ - \dfrac{1}{{1580.365.86400}}}}} \right) = 3,{70.10^{10}}\) hạt
Pôlôni \(^{210}Po\) là một chất phóng xạ có chu kì bán rã \(140\) ngày đêm. Hạt nhân pôlôni phóng xạ sẽ biến thành hạt nhân chì (\(^{206}Pb\)) và kèm theo một hạt a. Ban đầu có \(42 mg\) chất phóng xạ pôlôni. Khối lượng chì sinh ra sau \(280\) ngày đêm là:
-
A.
30,9 mg
-
B.
10,35 mg
-
C.
31,96 mg
-
D.
10,65 mg
Đáp án : A
- Khối lượng hạt nhân mẹ đã phân rã: \(\Delta {m_{m{\rm{e}}}}{\rm{ }} = {m_0}(1 - {2^{ - \dfrac{t}{T}}})\)
- Sử dụng công thức tính khối lượng hạt nhân con: \({m_{con}} = \dfrac{{\Delta {m_{me}}}}{{{A_{me}}}}.{A_{con}}\)
Ta có:
\({m_{Pb}} = \dfrac{{\Delta {m_{Po}}}}{{{A_{Po}}}}.{A_{Pb}} \\= {m_0}\dfrac{{{A_{Pb}}}}{{{A_{Po}}}}(1 - {2^{\dfrac{t}{T}}}) \\= 42\dfrac{{206}}{{210}}(1 - {2^{ - \dfrac{{280}}{{140}}}}) = 30,9mg\)
Đồng vị \({}_{11}^{24}\) Na là chất phóng xạ β- tạo thành hạt nhân magiê( \({}_{12}^{24}\)Mg). Ban đầu có 12gam Na và chu kì bán rã là 15 giờ. Sau 45 h thì khối lượng Mg tạo thành là :
-
A.
10,5 g
-
B.
5,16 g
-
C.
51,6 g
-
D.
0,516 g
Đáp án : A
- Khối lượng hạt nhân mẹ đã phân rã: \(\Delta {m_{m{\rm{e}}}}{\rm{ }} = {m_0}(1 - {2^{ - \frac{t}{T}}})\)
- Sử dụng công thức tính khối lượng hạt nhân con: \({m_{con}} = \frac{{\Delta {m_{me}}}}{{{A_{me}}}}.{A_{con}}\)
Nhận xét : t = 3T nên ta dùng hàm mũ 2 để giải cho nhanh bài toán :
- Khối lượng Na bị phân rã sau t = 45 giờ = 3T :
\(\begin{array}{l}\Delta m = {m_0}(1 - {2^{ - \dfrac{t}{T}}}) = 12(1 - {2^{ - 3}})\\ \leftrightarrow \Delta m{\rm{ }} = {\rm{ }}10,5{\rm{ }}g\end{array}\)
- Suy ra khối lượng của Mg tạo thành : \({m_{con}} = \dfrac{{\Delta {m_{me}}.{A_{con}}}}{{{A_{me}}}} = \frac{{10,5}}{{24}}.24 = 10,5g\)
Phương trình phóng xạ của Pôlôni có dạng:\({}_{84}^{210}Po\)\( \to {}_Z^APb + \alpha \).Cho chu kỳ bán rã của Pôlôni T=138 ngày. Khối lượng ban đầu m0=1g. Hỏi sau bao lâu khối lượng Pôlôni chỉ còn 0,707g?
-
A.
69 ngày
-
B.
138 ngày
-
C.
97,57 ngày
-
D.
195,19 ngày
Đáp án : A
Sử dụng công thức xác định khối lượng hạt nhân còn lại: \({\rm{m}} = {m_0}{e^{ - \lambda t}}\)
Tính t: \(\frac{m}{{{m_0}}} = {e^{ - \lambda .t}} \to t = \frac{{T.\ln \frac{{{m_0}}}{m}}}{{\ln 2}} = \frac{{138.\ln \frac{1}{{0,707}}}}{{\ln 2}}\) =69ngày
Một lượng chất phóng xạ sau 12 năm thì còn lại 1/16 khối lượng ban đầu của nó. Chu kì bán rã của chất đó là
-
A.
3 năm
-
B.
4,5 năm
-
C.
9 năm
-
D.
48 năm
Đáp án : A
Sử dụng công thức xác định khối lượng hạt nhân còn lại: \({\rm{m}} = {m_0}{2^{ - \frac{t}{T}}}\)
Ta có \(\frac{m}{{{m_0}}}\)=\(\frac{1}{{{2^{\frac{t}{T}}}}}\)=\(\frac{1}{{16}} = \frac{1}{{{2^4}}}\)
\( \to \frac{t}{T} = 4 \Rightarrow T = \frac{t}{4} = \frac{{12}}{4} = 3\) năm
Một đồng vị phóng xạ có chu kì bán rã T. Cứ sau một khoảng thời gian bằng bao nhiêu thì số hạt nhân bị phân rã trong khoảng thời gian đó bằng ba lần số hạt nhân còn lại của đồng vị ấy
-
A.
2T
-
B.
3T
-
C.
0,5T
-
D.
T
Đáp án : A
Sử dụng công thức xác định số hạt nhân còn lại: \({\rm{N}} = {N_0}{2^{ - \frac{t}{T}}}\)
- Sử dụng công thức tính số hạt bị phân rã: \(\Delta N{\rm{ }} = {N_0}(1 - {2^{ - \frac{t}{T}}}) = {N_0}\left( {1 - {e^{ - \lambda t}}} \right)\)
Theo đề , ta có :\(\Delta N = 3N\)
\(\frac{{\Delta N}}{N} = \frac{{{N_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right)}}{{{N_0}{{.2}^{ - \frac{t}{T}}}}} = 3 \Leftrightarrow {2^{\frac{t}{T}}} - 1 = 3 \Leftrightarrow {2^{\frac{t}{T}}} = 4 \Leftrightarrow t = 2T\)
\(_{11}^{24}Na\) là chất phóng xạ \({\beta ^ - }\) với chu kỳ bán rã 15 giờ. Ban đầu có một lượng \(_{11}^{24}Na\) thì sau một khoảng thời gian bao nhiêu lượng chất phóng xạ trên bị phân rã 75%?
-
A.
7h30'
-
B.
15h00'
-
C.
22h30'
-
D.
30h00'
Đáp án : D
Sử dụng công thức tính khối lượng hạt nhân bị phân rã: \(\Delta m = {m_0}(1 - {2^{ - \frac{t}{T}}})\)
Gọi m0 là khối lượng ban đầu của \(_{11}^{24}Na\)
Khối lượng chất phóng xạ đã bị phân rã:
\(\Delta m = {m_0}(1 - {2^{ - \frac{t}{T}}})\)
Theo đầu bài, ta có: ∆m=0,75m0
\( \to \dfrac{{\Delta m}}{{{m_0}}} = (1 - {2^{ - \dfrac{t}{T}}}) = 0,75 \to {2^{ - \dfrac{t}{T}}} = \dfrac{1}{4} \to \dfrac{t}{T} = 2 \to t = 2T = 30h00\)
Một lượng chất phóng xạ \({}_{86}^{222}Rn\) ban đầu có khối lượng 1mg. Sau 15,2 ngày độ phóng xạ giảm 93,75%. Chu kỳ bán rã của Rn là:
-
A.
4 ngày
-
B.
3,8 ngày
-
C.
3,5 ngày
-
D.
2,7 ngày
Đáp án : B
Sử dụng công thức tính độ phóng xạ: \(H = {H_0}{2^{ - \frac{t}{T}}}\)
Ta có: t = 15,2 ngày
Độ phóng xạ còn lại: H = 1-0,9375 = 0,0625
\(H = {H_0}{2^{ - \frac{t}{T}}} \to \frac{H}{{{H_0}}} = {2^{ - \frac{t}{T}}} = 0,0625 = \frac{1}{{16}} \to \frac{t}{T} = 4 \to T = \frac{t}{4} = \frac{{15,2}}{4} = 3,8{\rm{ }}ngày\)
Hạt nhân A (có khối lượng mA) đứng yên phóng xạ thành hạt B (có khối lượng mB) và C (có khối lượng mC) theo phương trình \(A \to B + C\). Nếu phản ứng tỏa năng lượng ∆E thì động năng của B là:
-
A.
\(\frac{{{m_B}}}{{{m_C} + {m_B}}}\Delta E\)
-
B.
\(\frac{{{m_C}}}{{{m_C} + {m_B}}}\Delta E\)
-
C.
\(\frac{{\left( {{m_C} + {m_B}} \right)}}{{{m_C}}}\Delta E\)
-
D.
\(\frac{{{m_B}}}{{{m_C}}}\Delta E\)
Đáp án : B
A phân rã => B + C
\(\left\{ \begin{array}{l}\overrightarrow {{P_t}} = \overrightarrow {{P_s}} \\{m_A}{c^2} = \left( {{m_B} + {m_C}} \right){c^2} + {{\rm{W}}_{{d_B}}} + {{\rm{W}}_{{d_C}}}\end{array} \right. \leftrightarrow \left\{ \begin{array}{l}0 = {m_B}\overrightarrow {{v_B}} + {m_C}\overrightarrow {{v_C}} \\\Delta E{\rm{ = }}{{\rm{W}}_{{d_B}}} + {{\rm{W}}_{{d_C}}}\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_{{d_B}}} = \frac{{{m_C}}}{{{m_B} + {m_C}}}\Delta E\\{{\rm{W}}_{{d_C}}} = \frac{{{m_B}}}{{{m_B} + {m_C}}}\Delta E\end{array} \right.\)
Hạt nhân \(A\) đang đứng yên thì phân rã thành hạt nhân \(B\) có khối lượng \(m_B\) và hạt $\alpha $ có khối lượng \(m_{\alpha}\). Tỉ số giữa động năng của hạt $\alpha $ và động năng của hạt nhân \(B\) ngay sau phân rã bằng:
-
A.
\({\left( {\dfrac{{{m_\alpha }}}{{{m_B}}}} \right)^2}\)
-
B.
\(\dfrac{{{m_B}}}{{{m_\alpha }}}\)
-
C.
\(\dfrac{{{m_\alpha }}}{{{m_B}}}\)
-
D.
\({\left( {\dfrac{{{m_B}}}{{{m_\alpha }}}} \right)^2}\)
Đáp án : B
\(A\) phân rã => \(B\) + \(\alpha\)
áp dụng định luật bảo toàn động lượng, ta có:
\(\begin{array}{l}\overrightarrow {{P_t}} = \overrightarrow {{P_s}} \leftrightarrow 0 = {m_B}\overrightarrow {{v_B}} + {m_\alpha }\overrightarrow {{v_\alpha }} \\ \to {m_B}\overrightarrow {{v_B}} = - {m_\alpha }\overrightarrow {{v_\alpha }} \end{array}\)
Mặt khác, ta có: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2} = \dfrac{{{P^2}}}{{2m}}\)
\(\begin{array}{l} \to P_B^2 = P_\alpha ^2 \leftrightarrow 2{m_B}{{\rm{W}}_{{d_B}}} = 2{m_\alpha }{{\rm{W}}_{{d_\alpha }}}\\\dfrac{{{{\rm{W}}_{{d_\alpha }}}}}{{{{\rm{W}}_{{d_B}}}}} = \dfrac{{{m_B}}}{{{m_\alpha }}}\end{array}\)
Chất phóng xạ \({}_{84}^{210}Po\) phát ra tia α và biến đổi thành \({}_{82}^{206}Pb\). Biết khối lượng các hạt là mPb = 205,9744u, mPo = 209,9828u, mα = 4,0026u. Giả sử hạt nhân mẹ ban đầu đứng yên và sự phân rã không phát ra tia γ thì động năng của hạt nhân con là
-
A.
0,1MeV
-
B.
0,02MeV
-
C.
0,01MeV
-
D.
0,2MeV
Đáp án : A
Xem lại dạng 6
- Sử dụng công thức xác định năng lượng tỏa ra: \(\Delta E = \left( {\sum {m{}_{trc} - \sum {{m_{sau}}} } } \right){c^2}\)
- 1uc2 = 931,5 MeV/c2
-Động năng của các hạt sau phân rã: \(\left\{ \begin{array}{l}{{\rm{W}}_{{d_B}}} = \frac{{{m_C}}}{{{m_B} + {m_C}}}\Delta E\\{{\rm{W}}_{{d_C}}} = \frac{{{m_B}}}{{{m_B} + {m_C}}}\Delta E\end{array} \right.\)
\[{}_{84}^{210}Po \to {}_{82}^{206}Pb + \alpha \]
Năng lượng tỏa ra:
\(\begin{array}{l}\Delta E = \left( {\sum {m{}_{trc} - \sum {{m_{sau}}} } } \right){c^2} = \left( {{m_{Po}} - \left( {{m_{Pb}} + {m_\alpha }} \right)} \right){c^2}\\ = \left( {209,9828u - (205,9744u + 4,0026u)} \right){c^2} = 5,{8.10^{ - 3}}u{c^2} = 5,4027MeV\end{array}\)
Động năng của hạt nhân Pb sau phân rã:
\({{\rm{W}}_{{d_{Pb}}}} = \frac{{{m_\alpha }}}{{{m_{Pb}} + {m_\alpha }}}\Delta E = \frac{{4,0026u}}{{205,9744u + 4,0026u}}5,4027MeV = 0,103MeV\)
Một hạt nhân X, ban đầu đứng yên, phóng xạ α và biến thành hạt nhân Y. Biết hạt nhân X có số khối là A, hạt α phát ra tốc độ v. Lấy khối lượng của hạt nhân bằng số khối của nó tính theo đơn vị u. Tốc độ của hạt nhân Y bằng:
-
A.
\(\frac{{2v}}{{A - 4}}\)
-
B.
\(\frac{{4v}}{{A + 4}}\)
-
C.
\(\frac{{2v}}{{A + 4}}\)
-
D.
\(\frac{{4v}}{{A - 4}}\)
Đáp án : D
\(_Z^AX \to _2^4\alpha + _{Z - 2}^{A - 4}Y\)
Áp dụng định luật bảo toàn động lượng, ta có:
\(\begin{array}{l}0 = {m_Y}\overrightarrow {{v_Y}} + {m_\alpha }\overrightarrow {{v_\alpha }} \to {m_Y}\overrightarrow {{v_Y}} = - {m_\alpha }\overrightarrow {{v_\alpha }} \\ \to {v_Y} = \frac{{{m_\alpha }{v_\alpha }}}{{{m_Y}}} = \frac{{4v}}{{A - 4}}\end{array}\)
\(_{92}^{235}U + _0^1n \to _{42}^{95}Mo + _{57}^{139}La + 2_0^1n + 7{e^ - }\) là một phản ứng phân hạch của Urani 235. Biết khối lượng hạt nhân : \({m_U} = {\rm{ }}234,99{\rm{ }}u\) ; \({m_{Mo}} = {\rm{ }}94,88{\rm{ }}u\) ;\({m_{La}} = {\rm{ }}138,87{\rm{ }}u\) ;\({m_n} = {\rm{ }}1,0087{\rm{ }}u\). Cho năng suất toả nhiệt của xăng là \({46.10^6}J/kg\). Khối lượng xăng cần dùng để có thể toả năng lượng tương đương với 1 gam U phân hạch ? Lấy \(1u{c^2} = 931MeV\)
-
A.
1616 kg
-
B.
1717 kg
-
C.
1818 kg
-
D.
1919 kg
Đáp án : D
- Sử dụng công thức xác định số hạt: \(N = \dfrac{{{m_A}}}{A}.{N_A}\)
- Năng lượng tỏa ra trong phản ứng: \(\Delta E{\rm{ }} = {\rm{ }}\left( {{\rm{ }}{M_0}-{\rm{ }}M{\rm{ }}} \right).{c^2}\)
Ta có:
\({m_U} = {\rm{ }}234,99{\rm{ }}u\)
\({m_{M0}} = {\rm{ }}94,88{\rm{ }}u\)
\({m_{La}} = {\rm{ }}138,87{\rm{ }}u\)
\({m_n} = {\rm{ }}1,0087{\rm{ }}u\)
\(q{\rm{ }} = {\rm{ }}{46.10^6}J/kg\)
Số hạt nhân nguyên tử 235U trong \(1g{\rm{ }}U\) là :
\(N = \dfrac{{{m_A}}}{A}.{N_A} = \dfrac{1}{{235}}.6,{02.10^{23}} = {\rm{ }}2,{5617.10^{21}}\) hạt
Năng lượng toả ra khi giải phóng hoàn toàn 1 hạt nhân U phân hạch là:
\(\begin{array}{l}\Delta E = \left( {{M_0} - M} \right){c^2}\\ = \left[ {\left( {{m_U} + {m_n}} \right) - \left( {{m_{Mo}} + {m_{La}} + 2{m_n}} \right)} \right]{c^2}\\ = \left[ {\left( {234,99u + 1,0087u} \right) - \left( {94,88u + 138,87u + 2.1,0087u} \right)} \right]{c^2}\\ = 0,2313u{c^2} = 215,3403MeV\end{array}\)
Năng lượng khi 1 gam U phản ứng phân hạch :
\(\begin{array}{l}E = \Delta E.N = 215,3403.2,{5617.10^{21}}\\ = 5,{5164.10^{23}}MeV = 8,{826.10^{10}}J\end{array}\)
Khối lượng xăng cần dùng để có năng lượng tương đương
\(m = \dfrac{{\Delta E}}{{{{46.10}^6}}} = \dfrac{{8,{{826.10}^{10}}}}{{{{46.10}^6}}} \approx 1919kg\)
Hiện nay trong quặng thiên nhiên có chứa cả \(_{92}^{238}U\) và \(_{92}^{235}U\) theo tỉ lệ nguyên tử là 140 :1. Giả sử ở thời điểm tạo thành Trái Đất, tỷ lệ trên là 1:1. Hãy tính tuổi của Trái Đất. Biết chu kỳ bán rã của \(_{92}^{238}U\) là 4,5.109 năm, \(_{92}^{235}U\) có chu kỳ bán rã 7,13.108 năm.
-
A.
60,4.108năm
-
B.
64.108 năm
-
C.
51,65.108 năm
-
D.
65.108 năm
Đáp án : A
Sử dụng công thức: \(N = {N_0}{2^{ - \frac{t}{T}}}\)
Gọi N0 là số nguyên tử của U238 và cũng là số nguyên tử của U235 ở thời điểm tạo thành trái đất.
Số nguyên tử của chúng tại thời điểm t: \({N_1} = {N_0}{2^{ - \frac{t}{{{T_1}}}}};{N_2} = {N_0}{2^{ - \frac{t}{{{T_2}}}}}\)
Theo đầu bài, ta có:
\(\begin{array}{l}\frac{{{N_1}}}{{{N_2}}} = 140 = \frac{{{2^{ - \frac{t}{{{T_1}}}}}}}{{{2^{ - \frac{t}{{{T_2}}}}}}} = {2^{\frac{t}{{{T_2}}} - \frac{t}{{{T_1}}}}} = 140 \to \frac{t}{{{T_2}}} - \frac{t}{{{T_1}}} = \log _2^{140} = 7,13\\ \to t\left( {\frac{1}{{{T_2}}} - \frac{1}{{{T_1}}}} \right) = 7,13 \to t = 60,{4.10^8}\end{array}\)
Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã \(T\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \({\rm{\Delta N}}\) và số hạt ban đầu \({{\rm{N}}_{\rm{0}}}{\rm{.}}\) Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này?

-
A.
\(5,6\) ngày
-
B.
\(8,9\) ngày
-
C.
\(3,8\) ngày
-
D.
\(138\) ngày
Đáp án : B
Áp dụng công thức tính số hạt còn lại trong mẫu sau thời gian t là:
\(N = {N_0}{e^{ - \lambda t}} = {N_0}{2^{\dfrac{{ - t}}{T}}}\)
Ta có: \(N = {N_0}{e^{ - \lambda t}} \Rightarrow \)Số hạt bị phân rã là:
\(\Delta N = {N_0} - {N_0}{e^{ - \lambda t}} = {N_0}(1 - {e^{ - \lambda t}})\)
\( \Rightarrow \dfrac{{\Delta N}}{{{N_0}}} = 1 - {e^{ - \lambda t}} \Rightarrow 1 - \dfrac{{\Delta N}}{{{N_0}}} = {e^{ - \lambda t}}\)
\( \Rightarrow \dfrac{1}{{\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)}} = {e^{\lambda t}} \Rightarrow \ln {\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \lambda t\)
Từ đồ thị ta thấy \(\lambda \approx 0,078\)
\( \Rightarrow T = \dfrac{{\ln 2}}{\lambda } \approx 8,9\) (ngày)
Hạt nhân Poloni \(\left( {_{84}^{210}Po} \right)\) đứng yên phát ra tia anpha và biến thành hạt nhân chì Pb. Cho \({m_{Po}} = 209,9828u\) , \({m_\alpha } = 4,0026u\), \({m_{Pb}} = 205,9744u\). Tốc độ của hạt nhân chì phóng ra bằng
-
A.
\(30,{6.10^5}m/s\)
-
B.
\({5.10^5}m/s\)
-
C.
\(3,{06.10^5}m/s\)
-
D.
\(3,{06.10^5}cm/s\)
Đáp án : C
+ Sử dụng công thức tính năng lượng phản ứng hạt nhân: \(\Delta E = \left( {{m_{Po}} - {m_\alpha } - {m_{Pb}}} \right).{c^2}\)
+ Áp dụng định luật bảo toàn động lượng
+ Sử dụng biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
Ta có: \(Po \to \alpha + Pb\)
\(\Delta E = \left( {{m_{Po}} - {m_\alpha } - {m_{Pb}}} \right).{c^2} = 5,{8.10^{ - 3}}u{c^2} = 5,4027MeV\)
Ta có: \({{\rm{W}}_{{d_\alpha }}} + {{\rm{W}}_{{d_{Pb}}}} = \Delta E\) (1)
Lại có: \(\overrightarrow {{P_{Po}}} = \overrightarrow {{P_\alpha }} + \overrightarrow {{P_{Pb}}} \)
Có \({v_{Po}} = 0 \Rightarrow {P_{Po}} = 0 \Rightarrow {P_\alpha } = {P_{Pb}}\)
\( \Rightarrow P_\alpha ^2 = P_{Pb}^2 \Rightarrow {m_\alpha }{{\rm{W}}_{{d_\alpha }}} = {m_{Pb}}{{\rm{W}}_{{d_{Pb}}}}\) (2)
Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}{{\rm{W}}_{{d_\alpha }}} = 5,29MeV\\{{\rm{W}}_{{d_{Pb}}}} = 0,1029MeV = 1,{6464.10^{ - 14}}J\end{array} \right.\)
Lại có \({{\rm{W}}_{{d_{Pb}}}} = \dfrac{1}{2}{m_{Pb}}v_{Pb}^2\)
\( \Rightarrow {v_{Pb}} = \sqrt {\dfrac{{2{W_{{d_{Pb}}}}}}{{{m_{Pb}}}}} = \sqrt {\dfrac{{2.1,{{6464.10}^{ - 14}}}}{{205,9744.1,{{66055.10}^{ - 27}}}}} = 3,{06.10^5}m/s\)
Coban \({}_{27}^{60}Co\) là chất phóng xạ có chu kì bán rã T = 5,33 năm. Lúc đầu có 1000g Co thì sau 10,66 năm số nguyên tử coban còn tại là?
-
A.
\(N = 2,{51.10^{24}}\)
-
B.
\(N = 5,{42.10^{22}}\)
-
C.
\(N = 8,{18.10^{20}}\)
-
D.
\(N = 1,{25.10^{21}}\)
Đáp án : A
Khối lượng hạt nhân còn lại: \(m = {m_0}{.2^{ - \dfrac{t}{T}}}\)
Công thức liên hệ giữa khối lượng và số hạt: \(N = \dfrac{m}{A}.{N_A}\)
Khối lượng Co còn lại sau 10,66 năm là:
\(m = {m_0}{.2^{ - \dfrac{t}{T}}} = {1000.2^{ - \dfrac{{10,66}}{{5,33}}}} = 250g\)
Số nguyên tử Coban còn lại là:
\(N = \dfrac{m}{A}.{N_A} = \dfrac{{250}}{{60}}.6,{02.10^{23}} = 2,{51.10^{24}}\)
Chất phóng xạ pôlôni \({}_{84}^{210}Po\) có chu kì bán rã 138 ngày. Ban đầu có một mẫu gồm N0 hạt nhân pôlôni \({}_{84}^{210}Po\). Sau bao lâu (kể từ lúc ban đầu), số hạt nhân \({}_{84}^{210}Po\) bị phân rã là \(\dfrac{7}{8}{N_0}\)?
-
A.
276 ngày.
-
B.
414 ngày.
-
C.
552 ngày.
-
D.
690 ngày.
Đáp án : B
Số hạt nhân còn lại: \(N = {N_0}{.2^{ - \dfrac{t}{T}}} = {N_0}.{e^{ - \lambda t}}\)
Số hạt nhân bị phân rã: \(\Delta N = {N_0}.\left( {1 - {2^{ - \dfrac{t}{T}}}} \right) = {N_0}.\left( {1.{e^{ - \lambda t}}} \right)\)
Số hạt nhân bị phân rã là: \(\Delta N = \dfrac{7}{8}{N_0}\)
Số hạt nhân còn lại là: \(N\left( t \right) = {N_0} - \Delta N = {N_0} - \dfrac{7}{8}{N_0} = \dfrac{1}{8}{N_0}\)
\( \Rightarrow {N_0}{.2^{ - \dfrac{t}{T}}} = \dfrac{1}{8}{N_0} \Rightarrow {2^{ - \dfrac{t}{T}}} = \dfrac{1}{8} = {2^{ - 3}} \Rightarrow \dfrac{t}{T} = 3 \Rightarrow t = 3T = 3.138 = 414\) (ngày)
Một chất phóng xạ có chu kì bán rã là 3,8 ngày. Số hạt nhân sẽ bị phân rã hết 70% sau thời gian là
-
A.
6,6 ngày.
-
B.
7,6 ngày.
-
C.
4,8 ngày.
-
D.
8,8 ngày.
Đáp án : A
Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: \(N = {N_0}{.2^{\frac{{ - t}}{T}}}\)
Số hạt nhân con được tạo thành hay số hạt nhân mẹ đã bị phân rã sau thời gian t được xác định bởi:
\(N' = {N_0} - N = {N_0}.(1 - {2^{\frac{{ - t}}{T}}})\)
Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: \(N = {N_0}{.2^{\frac{{ - t}}{T}}}\)
Số hạt nhân con được tạo thành hay số hạt nhân mẹ đã bị phân rã sau thời gian t được xác định bởi:
\(\begin{array}{l}
N' = {N_0} - N = {N_0}.(1 - {2^{\frac{{ - t}}{T}}}) = 70\% {N_0}\\
\Rightarrow (1 - {2^{\frac{{ - t}}{T}}}) = 70\% = 0,7 \Rightarrow {2^{\frac{{ - t}}{T}}} = 0,3\\
\Rightarrow t = - T.{\log _2}(0,3) = 1,74T = 1,74.3,8 = 6,6
\end{array}\)
Vậy thời gian là 6,6 ngày.
Trong điều trị bệnh ung thư, bệnh nhân được chiếu xạ với một liều xác định nào đó từ một nguồn phóng xạ. Biết nguồn có chu kỳ bán rã là 4 năm. Khi nguồn được sử dụng lần đầu thì thời gian cho 1 liều xạ là 10 phút. Hỏi sau hai năm thời gian cho 1 liều xạ là bao nhiêu phút:
-
A.
14
-
B.
10
-
C.
20
-
D.
7
Đáp án : A
Số hạt nhân bị phân rã: \(\Delta N = {N_0}.\left( {1 - {2^{ - \frac{t}{T}}}} \right)\,\)
Liều lượng phóng xạ cho một lần chiếu xạ trong các lần chiếu là không đổi (xác định).
Gọi \(\Delta N\) là liều lượng cho một lần chiếu xạ (∆N = hằng số)
Trong lần chiếu xạ đầu tiên: \(\Delta N = {N_{01}}.\left( {1 - {2^{ - \frac{{{t_1}}}{T}}}} \right)\,\,\,\left( 1 \right)\)
Trong lần chiếu xạ tiếp theo sau đó 2 năm: \(\Delta N = {N_{02}}.\left( {1 - {2^{ - \frac{{{t_2}}}{T}}}} \right)\)
Với: \({N_{02}} = {N_{01}}{.2^{ - \frac{{\Delta t}}{T}}} \Rightarrow \Delta N = {N_{01}}{.2^{ - \frac{{\Delta t}}{T}}}.\left( {1 - {2^{ - \frac{{{t_2}}}{T}}}} \right)\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \({N_{01}}{.2^{ - \frac{{\Delta t}}{T}}}.\left( {1 - {2^{ - \frac{{{t_2}}}{T}}}} \right) = {N_{01}}.\left( {1 - {2^{ - \frac{{{t_1}}}{T}}}} \right)\)
\( \Leftrightarrow {2^{ - \frac{{\Delta t}}{T}}}.\left( {1 - {2^{ - \frac{{{t_2}}}{T}}}} \right) = 1 - {2^{ - \frac{{{t_1}}}{T}}}\,\,\,\left( * \right)\)
Với: \(\left\{ \begin{array}{l}\Delta t = 2\,\left( {nam} \right)\\{t_1} = 10p\\T = 4\left( {\,nam} \right)\end{array} \right.\)
Thay vào (*) ta được: \({2^{ - \frac{2}{4}}}.\left( {1 - {2^{ - \frac{{{t_2}}}{{4.365.24.60}}}}} \right) = 1 - {2^{ - \frac{{10}}{{4.365.24.60}}}}\)
\( \Leftrightarrow {2^{ - \frac{{{t_2}}}{{4.365.24.60}}}} = 1 - \sqrt 2 .\left( {1 - {2^{ - \frac{{10}}{{4.365.24.60}}}}} \right) \Rightarrow {t_2} = 14,1phut\)
Gọi \({N_0}\) là số hạt nhân phóng xạ ban đầu \(\left( {t = 0} \right)\) và \(\Delta N\) là số hạt nhân đã phóng xạ sau thời gian \(t\). Đồ thị nào sau đây biểu thị sự biến thiên của \(\Delta N\) theo thời gian?

-
A.
Hình A
-
B.
Hình B
-
C.
Hình C
-
D.
Hình D
Đáp án : B
Số hạt nhân còn lại: \(N = {N_0}{.2^{ - \frac{t}{T}}}\)
Số hạt nhân đã bị phân rã: \(\Delta N = {N_0}.\left( {1 - {2^{ - \frac{t}{T}}}} \right)\)
Sử dụng lí thuyết về đồ thị hàm số.
Số hạt đã bị phân rã được xác định theo công thức:\(\Delta N = {N_0}.\left( {1 - {2^{ - \frac{t}{T}}}} \right)\)
Hàm số \(\Delta N = {N_0}.\left( {1 - {2^{ - \frac{t}{T}}}} \right)\) tăng từ 0 theo t và có tiệm cận ngang đi qua \({N_0}\).
\( \Rightarrow \) Đồ thị biểu diễn sự biến thiên của \(\Delta N\) theo thời gian là đồ thị B.
Các tế bào ung thư dễ bị tổn thương dưới tác dụng của tia X hoặc tia gamma hơn các tế bào khỏe mạnh. Mặc dù ngày nay đã có các máy gia tốc tuyến tính thay thế, nhưng trước kia nguồn tiêu chuẩn để điều trị là phóng xạ \({}^{60}Co\). Đồng vị này phân rã \(\beta \) thành \({}^{60}Ni\) ở trạng thái kích thích, nhưng \({}^{60}Ni\) ngay sau đó trở về trạng thái cơ bản và phát ra hai photon gamma, mỗi photon có năng lượng xấp xỉ 1,2 MeV. Biết rằng chu kì bán rã của phân rã \(\beta \) là 5,27 năm. Xác định số hạt nhân \({}^{60}Co\) có mặt trong nguồn 6000 Ci thường được dùng trong các bệnh viện.
-
A.
\(5,{33.10^{22}}\) hạt.
-
B.
\(3,{2.10^{14}}\) hạt.
-
C.
\(9,{98.10^{11}}\) hạt.
-
D.
\(3,{69.10^{22}}\) hạt.
Đáp án : A
Độ phóng xạ: \(H = N\lambda = N\dfrac{{\ln 2}}{T}\)
Độ phóng xạ của hạt nhân \({}^{60}Co\) là:
\(\begin{array}{l}H = N\dfrac{{\ln 2}}{T} \Rightarrow N = \dfrac{{H.T}}{{\ln 2}}\\ \Rightarrow N = \dfrac{{6000.3,{{7.10}^{10}}.5,27.365,25.86400}}{{\ln 2}} \approx 5,{33.10^{22}}\,\,\left( {hat} \right)\end{array}\)
Luyện tập và củng cố kiến thức Bài 38. Phản ứng phân hạch - nhiệt hạch Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập hạt nhân nguyên tử (phần 1) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập hạt nhân nguyên tử (phần 2) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 37. Phóng xạ Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập xác định động năng, vận tốc, góc của các hạt Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 36. Phản ứng hạt nhân Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 36. Năng lượng liên kết của hạt nhân Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 35. Tính chất và cấu tạo hạt nhân Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết










Danh sách bình luận