Bài tập trắc nghiệm Lí 12 có đáp án Bài tập trắc nghiệm Chương 4. Dao động và sóng điện từ

Trắc nghiệm Ôn tập chương 4 - Vật Lí 12

Đề bài

Xem đáp án

Làm bài tập

Đề bài

Câu 1 :

Tần số của dao động điện từ tự do trong mạch dao động LC có điện trở thuần không đáng kể được xác định bởi biểu thức:

A.

$f = \dfrac{1}{{2\pi \sqrt {LC} }}$
B.

$f = \dfrac{1}{{\sqrt {LC} }}$
C.

$f = \,\,\,\dfrac{1}{\pi }\sqrt {LC} $
D.

$f = \dfrac{{2\pi }}{{\sqrt {LC} }}$

Câu 2 :

Phát biểu nào sau đây không đúng khi nói về tính chất của sóng điện từ?

A.

Sóng điện từ có mang năng lượng.
B.

Tần số của sóng điện từ và tần số dao động của điện tích (gây ra sóng điện từ) bằng nhau.
C.

Sóng điện từ truyền trong chân không với vận tốc bằng vận tốc ánh sáng.
D.

Sóng điện từ không bị phản xạ ở tầng điện li của Trái Đất.

Câu 3 :

Sóng điện từ

A.

không truyền được trong chân không
B.

không mang năng lượng
C.

là sóng dọc
D.

là sóng ngang

Câu 4 :

Các sóng vô tuyến có thể xuyên qua tầng điện li có bước sóng cỡ :

A.

vài chục mét
B.

vài mét
C.

vài trăm mét
D.

vài nghìn mét

Câu 5 :

Trong mạch dao động LC lí tưởng có cuộn cảm thuần độ tự cảm là $8\mu {\rm{ }}H$ và tụ điện có điện dung là $2\mu F$. Chu kỳ dao động riêng của mạch bằng:

A.

$16\pi \mu s$
B.

$8\pi \mu s$
C.

$4\pi \mu s$
D.

$2\pi \mu s$

Câu 6 :

Sóng điện từ là quá trình lan truyền của điện từ trường biến thiên , trong không gian. Khi nói về quan hệ giữa điện trường và từ trường của điện từ trường trên kết luận nào sau đây là đúng.

A.

Điện trường và từ trường biến thiên theo thời gian với cùng chu kỳ
B.

Véc-tơ cường độ điện trường $\overrightarrow E $ và cảm ứng từ $\overrightarrow B $ cùng phương và cùng độ lớn
C.

Tại mỗi điểm của không gian, điện trường và từ trường luôn dao động lệch pha nhau $\dfrac{\pi }{2}$
D.

Tại mỗi điểm của không gian, điện trường và từ trường luôn dao động ngược pha

Câu 7 :

Tần số riêng dao động điện từ trong mạch LC là:

A.

$f = \sqrt {LC} $
B.

$f = 2\pi \sqrt {LC} $
C.

$f = \dfrac{1}{{2\pi \sqrt {LC} }}$
D.

$f = 2\pi \dfrac{L}{C}$

Câu 8 :

Phát biểu nào sai khi nói về sóng điện từ

A.

Trong sóng điện từ, điện trường và từ trường biến thiên theo thời gian với cùng chu kỳ.
B.

Trong sóng điện từ, điện trường và từ trường luôn dao động lệch pha nhau $\dfrac{\pi }{2}$.
C.

Sóng điện từ dùng trong thông tin vô tuyến gọi là sóng vô tuyến.
D.

Sóng điện từ là sự lan truyền trong không gian của điện từ trường biến thiên tuần hoàn theo thời gian.

Câu 9 :

Mạch dao động LC gồm cuộn cảm có độ tự cảm $L{\rm{ }} = {\rm{ }}2{\rm{ }}mH$ và tụ điện có điện dung $2{\rm{ }}pF$. Tần số dao động của mạch là:

A.

$2,5{\rm{ }}kHz$
B.

$2,5{\rm{ }}MHz$
C.

$1{\rm{ }}kHz$
D.

$1{\rm{ }}MHz$

Câu 10 :

Tần số góc của mạch dao động điện từ LC lý tưởng là:

A.

$\omega = \dfrac{1}{\pi }\sqrt {LC} $
B.

$\omega = \dfrac{1}{{\sqrt {LC} }}$
C.

$\omega = \dfrac{1}{{2\pi \sqrt {LC} }}$
D.

$\omega = \dfrac{{2\pi }}{{\sqrt {LC} }}$

Câu 11 :

Chọn câu sai khi nói về sóng điện từ?

A.

Sóng điện từ có thể phản xạ, nhiễu xạ, khúc xạ.
B.

Sóng điện từ mang năng lượng.
C.

Trong sóng điện từ, điện trường và từ trường biến thiên điều hòa cùng tần số và cùng pha với nhau.
D.

Sóng điện từ không truyền được trong chân không

Câu 12 :

Công thức tính năng lượng điện từ của mạch dao động LC lí tưởng là:

A.

$W{\rm{ }} = \dfrac{{Q_0^2}}{{2C}}$
B.

$W{\rm{ }} = \dfrac{{Q_0^2}}{{2L}}$
C.

$W{\rm{ }} = \dfrac{{Q_0^2}}{L}$
D.

$W{\rm{ }} = \dfrac{{Q_0^2}}{C}$

Câu 13 :

Gọi tốc độ truyền sóng điện từ trong không khí là $c$. Mạch dao động lý tưởng LC có thể phát ra sóng vô tuyến truyền trong không khí với bước sóng là:

A.

$\lambda = 2\pi c\sqrt {\dfrac{C}{L}} $
B.

$\lambda = 2\pi c\sqrt {LC} $
C.

$\lambda = 2\pi c\dfrac{1}{{\sqrt {LC} }}$
D.

$\lambda = 2\pi c\sqrt {\dfrac{L}{{{C^2}}}} $

Câu 14 :

Sóng $FM$ của đài Hà Nội có bước sóng $\lambda = \dfrac{{10}}{3}\left( m \right)$. Tìm tần số $f$?

A.

$90MHz$
B.

$100MHz$
C.

$80MHz$
D.

$60MHz$

Câu 15 :

Xone FM có tần số $102,7MHz$, sóng vô tuyến do đài này phát ra thuộc loại:

A.

sóng ngắn
B.

sóng dài
C.

sóng trung
D.

sóng cực ngắn

Câu 16 :

Trong sơ đồ khối của một máy phát thanh dùng sóng vô tuyến, không có bộ phận nào dưới đây?

A.

Mạch khuếch đại
B.

Mạch tách sóng
C.

Mạch biến điệu (trộn sóng)
D.

Anten phát

Câu 17 :

Sóng vô tuyến nào sau đây có thể xuyên qua tầng điện li?

A.

Sóng dài.
B.

Sóng ngắn.
C.

Sóng cực ngắn.
D.

Sóng trung.

Câu 18 :

Mạch dao động điện từ gồm cuộn cảm thuần $L$ và tụ điện có điện dung $C$ thay đổi được. Khi tăng điện dung của tụ điện lên $4$ lần thì chu kì dao động của mạch:

A.

tăng $4$ lần
B.

giảm $2$ lần
C.

tăng $2$ lần
D.

giảm $4$ lần

Câu 19 :

Sự biến thiên của dòng điện i trong mạch dao động lệch pha như thế nào so với sự biến thiên của điện tích q của một bản tụ điện ?

A.

$i$ trễ pha $\dfrac{\pi }{2}$ so với $q$
B.

$i$ cùng pha với $q$
C.

$i$ sớm pha $\dfrac{\pi }{2}$ so với $q$
D.

$i$ ngược pha với $q$

Câu 20 :

Cường độ dòng điện trong một mạch dao động LC lí tưởng có phương trình $i = 2cos\left( {{{2.10}^7}t{\rm{ }} + \dfrac{\pi }{2}} \right)\left( {mA} \right)$ (t tính bằng s). Điện tích của một bản tụ điện ở thời điểm $\dfrac{\pi }{{20}}\left( {\mu s} \right)$ có độ lớn là:

A.

$0,05{\rm{ }}nC$
B.

$0,1{\rm{ }}\mu C$
C.

$0,05{\rm{ }}\mu C$
D.

$0,1{\rm{ }}nC$

Câu 21 :

Một mạch dao động điện từ LC gồm cuộn dây thuần cảm có độ tự cảm không đổi và tụ điện có điện dung thay đổi được. Điện trở của dây dẫn không đáng kể và trong mạch có dao động điện từ riêng. Khi điện dung có giá trị ${C_1}$ thì tần số dao động riêng của mạch là ${f_1}$. Khi điện dung có giá trị ${C_2} = {\rm{ }}4{C_1}$ thì tần số dao động điện từ riêng trong mạch là:

A.

${f_2} = {\rm{ }}0,25{f_1}$
B.

${f_2} = {\rm{ }}2{f_1}$
C.

${f_2} = {\rm{ }}0,5{f_1}$
D.

${f_2} = {\rm{ }}4{f_1}$

Câu 22 :

Cho hai mạch dao động LC có cùng tần số. Điện tích cực đại của tụ ở mạch thứ nhất và thứ hai lần lượt là ${Q_1}$ và ${Q_2}$ thỏa mãn ${Q_1} + {\rm{ }}{Q_{2}} = {\rm{ }}{8.10^{ - 6}}$. Tại một thời điểm mạch thứ nhất có điện tích và cường độ dòng điện là ${q_1}$ và ${i_1}$, mạch thứ hai có điện tích và cường độ dòng điện là ${q_2}$ và ${i_2}$ thỏa mãn ${q_1}{i_2} + {\rm{ }}{q_2}{i_1} = {\rm{ }}{6.10^{ - 9}}$. Giá trị nhỏ nhất của tần số dao động ở hai mạch là:

A.

$63,66{\rm{ }}Hz$
B.

$76,39{\rm{ }}Hz$
C.

$38,19{\rm{ }}Hz$
D.

$59,68{\rm{ }}Hz$

Câu 23 :

Một mạch dao động LC gồm cuộn dây có $L{\rm{ }} = {\rm{ }}50mH$ và tụ điện có $C{\rm{ }} = {\rm{ }}5\mu F$. Nếu đoạn mạch có điện trở thuần $R{\rm{ }} = {\rm{ }}{10^{ - 2}}\Omega $, thì để duy trì dao động trong mạch luôn có giá trị cực đại của hiệu điện thế giữa hai bản tụ điện là ${U_0} = {\rm{ }}12V$. Ta phải cung cấp cho mạch một công suất là:

A.

$72nW$
B.

$72mW$
C.

$72\mu W$
D.

$7200W$

Câu 24 :

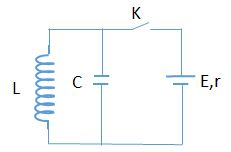
Cho mạch điện như hình vẽ bên, nguồn điện một chiều có suất điện động $E$ không đổi và điện trở trong $r$, cuộn dây thuần cảm $L$ và tụ điện có điện dung $C{\rm{ }} = {\rm{ }}2,{5.10^{ - 7}}F$. Ban đầu khoá $K$ mở, tụ chưa tích điện. Đóng khoá $K$, khi mạch ổn định thì mở khoá $K$. Lúc này trong mạch có dao động điện từ tự do với chu kì bằng $\pi {.10^{ - 6}}s$ và hiệu điện thế cực đại trên tụ bằng $2E$. Giá trị của $r$ gần với giá trị nào nhất sau đây?

A.

$2\Omega $
B.

$0,5\Omega $
C.

$1\Omega $
D.

$0,25\Omega $

Câu 25 :

Mạch dao động điện từ lí tưởng gồm một tụ điện có điện dung C và cuộn dây có hệ số tự cảm L. Biết cường độ dòng điện trong mạch có biểu thức $i = 0,04c{\rm{os}}{2.10^7}t(A)$. Điện tích cực đại của tụ có giá trị:

A.

${10^{ - 9}}C$
B.

${8.10^{ - 9}}C$
C.

${2.10^{ - 9}}C$
D.

${4.10^{ - 9}}C$

Câu 26 :

Có hai tụ điện ${C_1},{\rm{ }}{C_2}$ và hai cuộn cảm thuần ${L_1},{\rm{ }}{L_2}$. Biết ${C_1} = {\rm{ }}{C_2} = {\rm{ }}0,2\mu F$, ${L_1} = {L_2} = 2\mu H$. Ban đầu tích điện cho tụ ${C_1}$ đến hiệu điện thế $8V$ và tụ ${C_2}$ đến hiệu điện thế $16V$ rồi cùng một lúc mắc ${C_1}$ với ${L_1},{\rm{ }}{C_2}$ với ${L_2}$ để tạo thành mạch dao động lí tưởng ${L_1}{C_1}$ và ${L_2}{C_2}$. Lấy ${\pi ^{2}} = {\rm{ }}10$. Thời gian ngắn nhất kể từ khi hai mạch bắt đầu dao động đến khi hiệu điện thế trên hai tụ ${C_1}$ và ${C_2}$ chênh lệch nhau $4V$ là:

A.

$\dfrac{{{{10}^{ - 6}}}}{3}s$
B.

$\dfrac{{{{2.10}^{ - 6}}}}{3}s$
C.

$\dfrac{{{{10}^{ - 6}}}}{6}s$
D.

$\dfrac{{{{10}^{ - 6}}}}{{12}}s$

Câu 27 :

Một mạch dao động LC gồm tụ điện có điện dung $C{\rm{ }} = {\rm{ }}8nF$ và một cuộn dây thuần cảm có độ tự cảm $L{\rm{ }} = {\rm{ }}2mH$. Biết hiệu điện thế cực đại trên tụ là $6V$. Khi cường độ dòng điện trong mạch bằng $6mA$, thì hiệu điện thế giữa hai đầu cuộn cảm bằng:

A.

$4V$
B.

$3,6V$
C.

$3\sqrt 2 V$
D.

$3\sqrt 3 V$

Câu 28 :

Mạch chọn sóng của máy thu thanh gồm cuộn cảm $L$ và một tụ điện có thể thay đổi điện dung. Khi tụ điện có điện dung ${C_1}$, mạch thu được sóng điện từ có bước sóng $100m$; khi tụ đện có điện dung ${C_2}$, mạch thu được sóng điện từ có bước sóng $1km$. Tỉ số $\dfrac{{{C_2}}}{{{C_1}}}$ là:

A.

$10$
B.

0,1
C.

1000
D.

100

Câu 29 :

Tại một điểm có sóng điện từ truyền qua, cảm ứng từ biến thiên theo phương trình $B = {B_0}\cos (2\pi {.10^6}t)$ (t tính bằng s). Kể từ lúc $t{\rm{ }} = {\rm{ }}0$, thời điểm đầu tiên để cường độ điện trường tại điểm đó bằng $0$ là:

A.

$0,33{\rm{ }}\mu s$
B.

$0,25{\rm{ }}\mu s$
C.

$1,00{\rm{ }}\mu s$
D.

$0,50{\rm{ }}\mu s$

Câu 30 :

Một mạch dao động LC lí tưởng khi điện áp hai đầu bản tụ $u = 0,8{U_0}$ và tụ đang tích điện thì dòng điện trong mạch:

A.

$\dfrac{{3{U_0}}}{5}\sqrt {\dfrac{C}{L}} $ đang giảm
B.

$\dfrac{{3{U_0}}}{5}\sqrt {\dfrac{C}{L}} $ đang tăng
C.

$\dfrac{{4{U_0}}}{5}\sqrt {\dfrac{C}{L}} $ đang giảm
D.

$\dfrac{{4{U_0}}}{5}\sqrt {\dfrac{C}{L}} $ đang tăng

Câu 31 :

Cho một mạch đang có dao động điện tử. Nếu cứ sau mỗi chu kì dao động, năng lượng điện tử toàn phần giảm $19\% $ thì biên độ dòng điện giảm?

A.

7%
B.

6%
C.

10%
D.

4%

Câu 32 :

Trong mạch dao động LC. Tính độ lớn của cường độ dòng điện $i$ đi qua cuộn dây khi năng lượng điện trường của tụ điện bằng $n$ lần năng lượng từ trường của cuộn dây. Biết cường độ cực đại đi qua cuộn dây là ${I_0}$:

A.

$i = \dfrac{{{I_0}}}{n}$
B.

$i = \pm \dfrac{{{I_0}}}{{\sqrt {n + 1} }}$
C.

$i = {\rm{ }}{I_0}$
D.

$i = \pm \sqrt {\dfrac{n}{{n + 1}}} {I_0}$

Câu 33 :

Mạch dao động $LC$ lí tưởng có độ tự cảm $L$ không đổi. khi tụ điện có điện dung ${C_1}$ thì tần số dao động riêng của mạch là ${f_1} = {\rm{ }}75MHz$. Khi ta thay tụ ${C_1}$ bằng tụ ${C_2}$ thì tần số dao động riêng của mạch là ${f_2} = 50\sqrt {10} MHz$. Nếu ta dùng ${C_1}$ nối tiếp ${C_2}$ thì tần số dao động riêng $f$của mạch là:

A.

$175MHz$
B.

$125MHz$
C.

$25MHz$
D.

$87,5MHz$

Câu 34 :

Mạch dao động gồm cuộn cảm $L$ và tụ điện ${C_1}$ có chu kì dao động ${5.10^{ - 5}}s$. Mạch dao động gồm cuộn cảm $L$ và tụ điện ${C_2}$ có chu kì dao động $1,{2.10^{ - 4}}s$. Nếu mạch dao động gồm cuộn cảm $L$ và bộ tụ điện ${C_1}$ song song ${C_2}$ thì chu kì dao động là:

A.

$1,{3.10^{ - 4}}s$
B.

$1,{7.10^{ - 4}}s$
C.

$3,{4.10^{ - 5}}s$
D.

${7.10^{ - 5}}s$

Câu 35 :

Một mạch dao động điện từ $LC$ lí tưởng gồm cuộn cảm thuần có độ tự cảm $5mH$ và tụ điện có điện dung $5nF$. Trong mạch có dao động điện từ tự do. Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là:

A.

$2,5\pi {.10^{ - 6}}s$
B.

$10\pi {.10^{ - 6}}s$
C.

${10^{ - 6}}s$
D.

$5\pi {.10^{ - 6}}s$

Câu 36 :

Một mạch dao động gồm cuộn dây thuần cảm có độ tự cảm $L$ và tụ điện có điện dung $C$ thực hiện dao động điện từ tự do. Điện tích cực đại trên mỗi bản tụ là ${Q_0}$ và cường độ dòng điện cực đại trong mạch là ${I_0}$. Chu kỳ dao động điện từ của mạch là:

A.

$T = 2\pi {Q_0}{I_0}$
B.

$T = 2\pi \dfrac{{{I_0}}}{{{Q_0}}}$
C.

$T = 2\pi LC$
D.

$T = 2\pi \dfrac{{{Q_0}}}{{{I_0}}}$

Câu 37 :

Một mạch dao động $LC$ lí tưởng gồm cuộn cảm thuần $L$ và tụ điện $C$ có hai bản $A$ và $B$. Trong mạch đang có dao động điện từ tự do với chu kì $T$, biên độ điện tích của tụ điện bằng ${Q_0}$. Tại thời điểm $t$, điện tích bản $A$ là ${q_A} = \dfrac{{{Q_0}}}{2}$ và đang tăng. Sau khoảng thời gian $\Delta t$ nhỏ nhất thì điện tích của bản $B$ là ${q_B} = {\rm{ }}{Q_0}$. Giá trị của $\Delta t$ là:

A.

$\dfrac{T}{6}$
B.

$\dfrac{{2T}}{3}$
C.

$\dfrac{{5T}}{{12}}$
D.

$\dfrac{T}{3}$

Câu 38 :

Một mạch dao động $LC$ lí tưởng gồm cuộn dây thuần cảm có $L{\rm{ }} = {\rm{ }}2mH$ và tụ điện có điện dung $C{\rm{ }} = 2nF$. Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì dòng điện trong mạch có độ lớn $\sqrt 2 A$. Lấy gốc thời gian là lúc dòng điện trong mạch có giá trị bằng một nửa giá trị cực đại và tụ đang phóng điện. Biểu thức của cường độ dòng điện trong mạch là:

A.

$i = 2\cos ({5.10^5}t - \dfrac{\pi }{3})A$
B.

$i = 2\cos ({5.10^5}t - \dfrac{{2\pi }}{3})A$
C.

$i = 2\cos ({5.10^5}t + \dfrac{{2\pi }}{3})A$
D.

$i = 2\cos ({5.10^5}t + \dfrac{\pi }{3})A$

Câu 39 :

Một tụ xoay có điện dung biến thiên theo hàm số bậc nhất với góc quay từ giá trị ${C_{1}} = {\rm{ }}10pF$ đến ${C_{2}} = {\rm{ }}370pF$ tương ứng góc quay của các bản tăng dần từ ${0^0}$ đến ${180^0}$. Tụ điện được mắc với một cuộn dây thuần cảm có $L{\rm{ }} = {\rm{ }}2mH$ để tạo thành mạch chọn sóng của máy thu. Để thu được bước sóng 22,3m thì phải xoay tụ một góc bằng bao nhiêu kể từ vị trí điện dung cực đại.

A.

${120^0}$
B.

${150^0}$
C.

${60^0}$
D.

${30^0}$

Câu 40 :

Trong mạch dao động $LC$ lí tưởng với cường độ dòng điện cực đại là ${I_0}$ và dòng điện biến thiên với tần số góc bằng $\omega $. Trong khoảng thời gian cường độ dòng điện giảm từ giá trị cực đại đến một nửa cực đại thì điện lượng chuyển qua cuộn dây có độ lớn bằng:

A.

$\dfrac{{\sqrt 3 {I_0}}}{{2\omega }}$
B.

$\dfrac{{{I_0}}}{{2\omega }}$
C.

$\dfrac{{\sqrt 3 {I_0}\omega }}{2}$
D.

$\dfrac{{{I_0}\omega }}{2}$

Câu 41 :

Một sóng điện từ truyền trong chân không với bước sóng $150{\rm{ }}m$, cường độ điện trường cực đại và cảm ứng từ cực đại của sóng lần lượt là ${E_0}$ và ${B_0}$.Tại thời điểm nào đó, cường độ điện trường tại một điểm trên phương truyền sóng có giá trị $\dfrac{{{E_0}\sqrt 3 }}{2}$ và đang tăng. Sau thời gian ngắn nhất là bao nhiêu thì cảm ứng từ tại điểm đó có giá trị bằng $\dfrac{{{B_0}}}{2}$?

A.

$\dfrac{{250}}{3}ns$
B.

$62,5{\rm{ }}ns$
C.

$\dfrac{{500}}{3}ns$
D.

$125{\rm{ }}ns$

Câu 42 :

Trong nguyên tắc thông tin liên lạc bằng sóng vô tuyến, biến điệu sóng là:

A.

biến dao động âm thành dao động điện âm tần.
B.

làm cho biên độ sóng giảm xuống.
C.

trộn sóng âm tần với sóng cao tần.
D.

tách sóng âm tần ra khỏi sóng cao tần.

Câu 43 :

Trong một mạch dao động $LC$ lí tưởng, cường độ dòng điện trong mạch có biểu thức $i = 0,4\cos \left( {{{2.10}^6}t - \dfrac{\pi }{2}} \right)A$. Điện tích trên tụ có biểu thức là:

A.

$q{\rm{ }} = {\rm{ }}0,2cos\left( {{{2.10}^6}t{\rm{ }}} \right)\left( {nC} \right)$
B.

$q{\rm{ }} = {\rm{ }}0,2cos\left( {{{2.10}^6}t} \right)\left( {\mu C} \right)$
C.

$q{\rm{ }} = {\rm{ }}0,2cos\left( {{{2.10}^6}t{\rm{ }} - {\rm{ }}\pi } \right)\left( {\mu C} \right)$
D.

$q{\rm{ }} = {\rm{ }}0,2cos\left( {{{2.10}^6}1{\rm{ }} - \pi } \right)\left( {nC} \right)$

Câu 44 :

Một vật phát sóng điện từ dùng mạch $LC$ lý tưởng. Biết điện tích cực đại trên một bản tụ là 2nC và dòng điện cực đại qua cuộn cảm là $0,3A$. Sóng điện từ do mạch dao độn này phát ra thuộc loại:

A.
Sóng dài
B.
Sóng cực ngắn
C.
Sóng trung
D.
Sóng ngắn

Lời giải và đáp án

Câu 1 :

Tần số của dao động điện từ tự do trong mạch dao động LC có điện trở thuần không đáng kể được xác định bởi biểu thức:

A.

$f = \dfrac{1}{{2\pi \sqrt {LC} }}$
B.

$f = \dfrac{1}{{\sqrt {LC} }}$
C.

$f = \,\,\,\dfrac{1}{\pi }\sqrt {LC} $
D.

$f = \dfrac{{2\pi }}{{\sqrt {LC} }}$

Đáp án : A

Lời giải chi tiết :

Tần số của mạch dao động LC: $f = \dfrac{1}{{2\pi \sqrt {LC} }}$

Câu 2 :

Phát biểu nào sau đây không đúng khi nói về tính chất của sóng điện từ?

A.

Sóng điện từ có mang năng lượng.
B.

Tần số của sóng điện từ và tần số dao động của điện tích (gây ra sóng điện từ) bằng nhau.
C.

Sóng điện từ truyền trong chân không với vận tốc bằng vận tốc ánh sáng.
D.

Sóng điện từ không bị phản xạ ở tầng điện li của Trái Đất.

Đáp án : D

Lời giải chi tiết :

A, B, C – đúng

D – sai vì sóng điện từ bị phản xạ ở tầng điện li của Trái Đất

Câu 3 :

Sóng điện từ

A.

không truyền được trong chân không
B.

không mang năng lượng
C.

là sóng dọc
D.

là sóng ngang

Đáp án : D

Lời giải chi tiết :

A – sai vì: sóng điện từ truyền được trong chân không

B – sai vì: sóng điện từ mang năng lượng

C – sai vì sóng điện từ là sóng ngang

D – đúng: Sóng điện từ là sóng ngang

Câu 4 :

Các sóng vô tuyến có thể xuyên qua tầng điện li có bước sóng cỡ :

A.

vài chục mét
B.

vài mét
C.

vài trăm mét
D.

vài nghìn mét

Đáp án : B

Phương pháp giải :

Vận dụng bảng bước sóng vô tuyến và ứng dụng

Lời giải chi tiết :

Từ bảng bước sóng vô tuyến và ứng dụng:

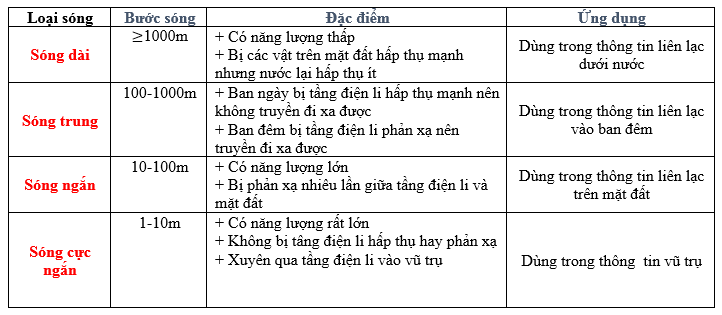
=> Sóng vô tuyến có thể xuyên qua tầng điện li là sóng cực ngắn có bước sóng cỡ $1 - 10m$

=> Các sóng vô tuyến có thể xuyên qua tầng điện li có bước sóng cỡ vài mét

Câu 5 :

A.

$16\pi \mu s$
B.

$8\pi \mu s$
C.

$4\pi \mu s$
D.

$2\pi \mu s$

Đáp án : B

Phương pháp giải :

Sử dụng biểu thức tính chu kì dao động của mạch LC: $T = 2\pi \sqrt {LC} $

Lời giải chi tiết :

Chu kỳ dao động của mạch LC : $T = 2\pi \sqrt {LC} = 2\pi \sqrt {{{8.10}^{ - 6}}{{.2.10}^{ - 6}}} = 8\pi \,\left( {\mu s} \right)$

Câu 6 :

A.

Điện trường và từ trường biến thiên theo thời gian với cùng chu kỳ
B.

Véc-tơ cường độ điện trường $\overrightarrow E $ và cảm ứng từ $\overrightarrow B $ cùng phương và cùng độ lớn
C.

Tại mỗi điểm của không gian, điện trường và từ trường luôn dao động lệch pha nhau $\dfrac{\pi }{2}$
D.

Tại mỗi điểm của không gian, điện trường và từ trường luôn dao động ngược pha

Đáp án : A

Lời giải chi tiết :

A – đúng

B – sai vì: Véc-tơ cường độ điện trường $\overrightarrow E $ và cảm ứng từ $\overrightarrow B $ luôn vuông góc với nhau và vuông góc với phương truyền sóng

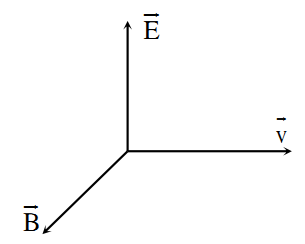
C, D – sai vì: điện trường và từ trường dao động cùng pha với nhau

Câu 7 :

Tần số riêng dao động điện từ trong mạch LC là:

A.

$f = \sqrt {LC} $
B.

$f = 2\pi \sqrt {LC} $
C.

$f = \dfrac{1}{{2\pi \sqrt {LC} }}$
D.

$f = 2\pi \dfrac{L}{C}$

Đáp án : C

Lời giải chi tiết :

Tần số của mạch dao động LC: $f = \dfrac{1}{{2\pi \sqrt {LC} }}$

Câu 8 :

Phát biểu nào sai khi nói về sóng điện từ

A.

Trong sóng điện từ, điện trường và từ trường biến thiên theo thời gian với cùng chu kỳ.
B.

Trong sóng điện từ, điện trường và từ trường luôn dao động lệch pha nhau $\dfrac{\pi }{2}$.
C.

Sóng điện từ dùng trong thông tin vô tuyến gọi là sóng vô tuyến.
D.

Sóng điện từ là sự lan truyền trong không gian của điện từ trường biến thiên tuần hoàn theo thời gian.

Đáp án : B

Lời giải chi tiết :

Trong sóng điện từ thì điện trường và từ trường luôn dao động cùng pha nhau

Câu 9 :

Mạch dao động LC gồm cuộn cảm có độ tự cảm $L{\rm{ }} = {\rm{ }}2{\rm{ }}mH$ và tụ điện có điện dung $2{\rm{ }}pF$. Tần số dao động của mạch là:

A.

$2,5{\rm{ }}kHz$
B.

$2,5{\rm{ }}MHz$
C.

$1{\rm{ }}kHz$
D.

$1{\rm{ }}MHz$

Đáp án : B

Phương pháp giải :

Sử dụng biểu thức tính tần số mạch dao động LC: $f = \dfrac{1}{{2\pi \sqrt {LC} }}$

Lời giải chi tiết :

Tần số dao động của mạch LC là: $f = \dfrac{1}{{2\pi \sqrt {LC} }} = \dfrac{1}{{2\pi \sqrt {{{2.10}^{ - 3}}{{.2.10}^{ - 12}}} }} = 2,{5.10^6}(Hz) = 2,5(MHz)$

Câu 10 :

Tần số góc của mạch dao động điện từ LC lý tưởng là:

A.

$\omega = \dfrac{1}{\pi }\sqrt {LC} $
B.

$\omega = \dfrac{1}{{\sqrt {LC} }}$
C.

$\omega = \dfrac{1}{{2\pi \sqrt {LC} }}$
D.

$\omega = \dfrac{{2\pi }}{{\sqrt {LC} }}$

Đáp án : B

Lời giải chi tiết :

Tần số góc của mạch dao động LC lí tưởng là: $\omega = \dfrac{1}{{\sqrt {LC} }}$

Câu 11 :

Chọn câu sai khi nói về sóng điện từ?

A.

Sóng điện từ có thể phản xạ, nhiễu xạ, khúc xạ.
B.

Sóng điện từ mang năng lượng.
C.

Trong sóng điện từ, điện trường và từ trường biến thiên điều hòa cùng tần số và cùng pha với nhau.
D.

Sóng điện từ không truyền được trong chân không

Đáp án : D

Lời giải chi tiết :

A, B, C - đúng

D – sai vì: Sóng điện từ truyền được trong chân không

Câu 12 :

Công thức tính năng lượng điện từ của mạch dao động LC lí tưởng là:

A.

$W{\rm{ }} = \dfrac{{Q_0^2}}{{2C}}$
B.

$W{\rm{ }} = \dfrac{{Q_0^2}}{{2L}}$
C.

$W{\rm{ }} = \dfrac{{Q_0^2}}{L}$
D.

$W{\rm{ }} = \dfrac{{Q_0^2}}{C}$

Đáp án : A

Lời giải chi tiết :

Năng lượng điện từ của mạch dao động LC lí tưởng: ${\rm{W}} = \dfrac{1}{2}CU_0^2 = \dfrac{1}{2}\dfrac{{Q_0^2}}{C} = \dfrac{1}{2}LI_0^2$

Câu 13 :

Gọi tốc độ truyền sóng điện từ trong không khí là $c$. Mạch dao động lý tưởng LC có thể phát ra sóng vô tuyến truyền trong không khí với bước sóng là:

A.

$\lambda = 2\pi c\sqrt {\dfrac{C}{L}} $
B.

$\lambda = 2\pi c\sqrt {LC} $
C.

$\lambda = 2\pi c\dfrac{1}{{\sqrt {LC} }}$
D.

$\lambda = 2\pi c\sqrt {\dfrac{L}{{{C^2}}}} $

Đáp án : B

Phương pháp giải :

Sử dụng biểu thức tính bước sóng $\lambda = cT$

Lời giải chi tiết :

Biểu thức tính bước sóng: $\lambda = 2\pi c\sqrt {LC} $

Câu 14 :

Sóng $FM$ của đài Hà Nội có bước sóng $\lambda = \dfrac{{10}}{3}\left( m \right)$. Tìm tần số $f$?

A.

$90MHz$
B.

$100MHz$
C.

$80MHz$
D.

$60MHz$

Đáp án : A

Phương pháp giải :

Vận dụng công thức tính bước sóng điện từ: $\lambda = \dfrac{v}{f}$

Lời giải chi tiết :

Sóng FM của đài Hà Nội là sóng điện từ lan truyền trong không gian với vận tốc $c{\rm{ }} = {\rm{ }}{3.10^8}m/s$

→ Tần số : $f = \dfrac{v}{\lambda } = {\rm{ }}\dfrac{{{{3.10}^8}}}{{\dfrac{{10}}{3}}} = {90.10^6}Hz = 90{\rm{ }}MHz$

Câu 15 :

Xone FM có tần số $102,7MHz$, sóng vô tuyến do đài này phát ra thuộc loại:

A.

sóng ngắn
B.

sóng dài
C.

sóng trung
D.

sóng cực ngắn

Đáp án : D

Phương pháp giải :

+ Sử dụng biểu thức tính bước sóng: $\lambda = \dfrac{c}{f}$

+ Vận dụng bảng bước sóng vô tuyến:

Lời giải chi tiết :

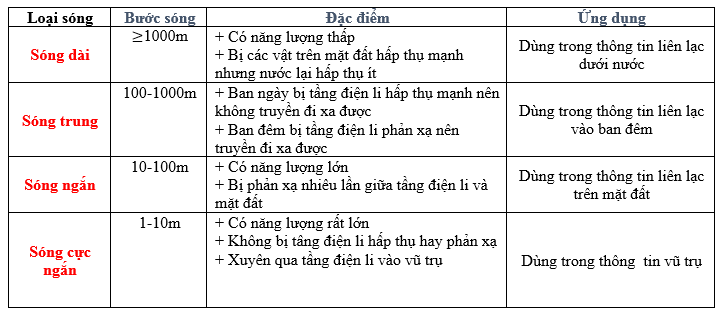
Ta có:

Bước sóng của sóng sóng $\lambda = \dfrac{c}{f} = \dfrac{{{{3.10}^8}}}{{102,{{7.10}^6}}} = 2,92m$ thuộc dải sóng cực ngắn

=> Sóng do đài này phát ra thuộc sóng cực ngắn

Câu 16 :

Trong sơ đồ khối của một máy phát thanh dùng sóng vô tuyến, không có bộ phận nào dưới đây?

A.

Mạch khuếch đại
B.

Mạch tách sóng
C.

Mạch biến điệu (trộn sóng)
D.

Anten phát

Đáp án : B

Phương pháp giải :

Sử dụng sơ đồ khối của máy phát thanh:

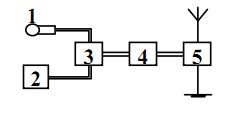
1 - Micro: Tạo ra dao động điện từ âm tần.

2 - Mạch phát sóng điện từ cao tần: Phát sóng điện từ có tần số cao.

3 - Mạch biến điệu: Trộn dao động điện từ cao tần với dao động điện từ âm tần.

4 - Mạch khuếch đại: Khuếch đại dao động điện từ cao tần đã được biến điệu.

5 - Anten phát: Tạo ra điện từ trường cao tần lan truyền trong không gian.

Lời giải chi tiết :

Ta có, sơ đồ khối của máy phát thanh:

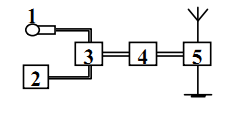
1 - Micro: Tạo ra dao động điện từ âm tần.

2 - Mạch phát sóng điện từ cao tần: Phát sóng điện từ có tần số cao.

3 - Mạch biến điệu: Trộn dao động điện từ cao tần với dao động điện từ âm tần.

4 - Mạch khuếch đại: Khuếch đại dao động điện từ cao tần đã được biến điệu.

5 - Anten phát: Tạo ra điện từ trường cao tần lan truyền trong không gian.

=> Trong sơ đồ khối của một máy phát thanh dùng sóng vô tuyến, không có mạch tách sóng

Câu 17 :

Sóng vô tuyến nào sau đây có thể xuyên qua tầng điện li?

A.

Sóng dài.
B.

Sóng ngắn.
C.

Sóng cực ngắn.
D.

Sóng trung.

Đáp án : C

Phương pháp giải :

Sử dụng bảng sóng vô tuyến – đặc điểm - ứng dụng

Lời giải chi tiết :

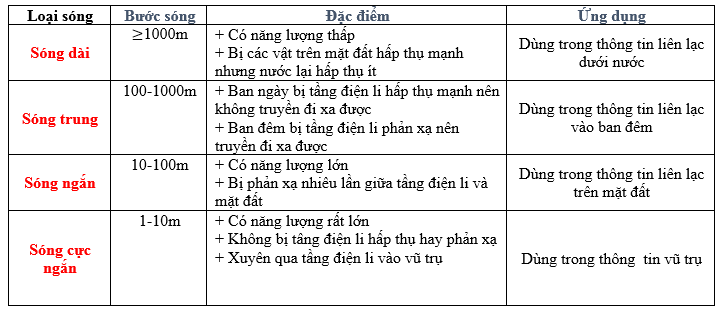
Từ bảng sóng vô tuyến và đặc điểm:

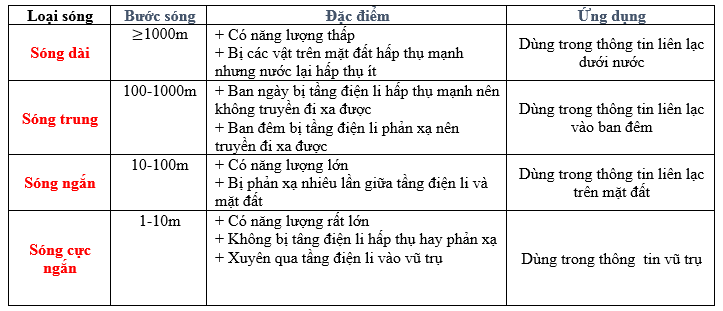
=> Sóng cực ngắn có thể xuyên qua tầng điện li

Câu 18 :

A.

tăng $4$ lần
B.

giảm $2$ lần
C.

tăng $2$ lần
D.

giảm $4$ lần

Đáp án : C

Phương pháp giải :

Sử dụng biểu thức tính chu kì dao động của mạch LC: $T = 2\pi \sqrt {LC} $

Lời giải chi tiết :

Ta có chu kì dao động của mạch: $T = 2\pi \sqrt {LC} $

=> Khi C tăng lên $4$ lần thì chu kì $T$ sẽ tăng lên $2$ lần

Câu 19 :

Sự biến thiên của dòng điện i trong mạch dao động lệch pha như thế nào so với sự biến thiên của điện tích q của một bản tụ điện ?

A.

$i$ trễ pha $\dfrac{\pi }{2}$ so với $q$
B.

$i$ cùng pha với $q$
C.

$i$ sớm pha $\dfrac{\pi }{2}$ so với $q$
D.

$i$ ngược pha với $q$

Đáp án : C

Phương pháp giải :

Sử dụng lí thuyết về phương trình của $q$ và $i$ :$\left\{ \begin{array}{l}q = {Q_0}{\rm{cos}}\left( {\omega t + \varphi } \right)\\i = q'\end{array} \right.$

Lời giải chi tiết :

Ta có: $\left\{ \begin{array}{l}q = {Q_0}\cos \left( {\omega t + \varphi } \right)\\i = q' = - \omega {Q_0}\sin \left( {\omega t + \varphi } \right) = {I_0}\cos \left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\end{array} \right.$

=> $i$ sớm pha $\dfrac{\pi }{2}$ so với $q$

Câu 20 :

A.

$0,05{\rm{ }}nC$
B.

$0,1{\rm{ }}\mu C$
C.

$0,05{\rm{ }}\mu C$
D.

$0,1{\rm{ }}nC$

Đáp án : D

Phương pháp giải :

+ Sử dụng hệ thức vuông pha của i và q: ${\left( {\dfrac{i}{{{I_0}}}} \right)^2} + {\left( {\dfrac{q}{{{Q_0}}}} \right)^2} = 1$

+ Vận dụng biểu thức cường độ dòng điện cực đại: ${I_0} = \omega {Q_0}$

Lời giải chi tiết :

Ta có: ${\left( {\dfrac{i}{{{I_0}}}} \right)^2} + {\left( {\dfrac{q}{{{Q_0}}}} \right)^2} = 1$

Tại : $t = \frac{{\pi {\rm{}}}}{{20}}\mu s$ thay vào phương trình $i$ , ta có:

$i{\rm{ }} = 2\cos \left( {{{2.10}^7}.\dfrac{\pi }{{20}}{{.10}^{ - 6}} + \dfrac{\pi }{2}} \right) = 0\left( A \right)$

$ \to q = {Q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{{{2.10}^{ - 3}}}}{{{{2.10}^7}}} = {10^{ - 10}}C = 0,1nC$

Câu 21 :

A.

${f_2} = {\rm{ }}0,25{f_1}$
B.

${f_2} = {\rm{ }}2{f_1}$
C.

${f_2} = {\rm{ }}0,5{f_1}$
D.

${f_2} = {\rm{ }}4{f_1}$

Đáp án : C

Phương pháp giải :

Sử dụng công thức tính tần số dao động: $f = \dfrac{1}{{2\pi \sqrt {LC} }}$

Lời giải chi tiết :

Ta có: $\left\{ \begin{array}{l}{f_1} = \dfrac{1}{{2\pi \sqrt {L{C_1}} }}\\{f_2} = \dfrac{1}{{2\pi \sqrt {L{C_2}} }} = \dfrac{1}{{2\pi \sqrt {L.4{C_1}} }} = \dfrac{{{f_1}}}{2} = 0,5{f_1}\end{array} \right.$

Câu 22 :

A.

$63,66{\rm{ }}Hz$
B.

$76,39{\rm{ }}Hz$
C.

$38,19{\rm{ }}Hz$
D.

$59,68{\rm{ }}Hz$

Đáp án : D

Phương pháp giải :

+ Vận dụng giá trị của hàm $\sin ,c{\rm{os}}$ : $\left| {{\rm{cosx}}} \right| \le 1$

+ Vận dụng BĐT cosi: $a + b \ge 2\sqrt {ab} $

+ Sử dụng biểu thức tính tần số: $f = \dfrac{\omega }{{2\pi }}$

Lời giải chi tiết :

Gọi độ lệch pha giữa ${q_1}$ và ${q_2}$ là $\Delta \varphi $

Tại thời điểm ${q_1} = 0$ thì ${i_1} = {I_{o1}} = {Q_1}\omega $ và ${q_2} = {Q_2}cos\Delta \varphi $ thay vào phương trình ${q_1}{i_2} + {q_2}{i_1} = {6.10^{ - 9}}$ ta được:

${Q_1}{Q_2}\omega cos\Delta \varphi {\rm{}} = {6.10^{ - 9}} \to \omega {\rm{}} = \frac{{{{6.10}^{ - 9}}}}{{{Q_1}{Q_2}cos\Delta \varphi }}$

Ta có:

$\begin{array}{l}{Q_1} + {Q_2} \ge 2\sqrt {{Q_1}{Q_2}} \\ \to {Q_1}{Q_2} \le \dfrac{{{{\left( {{Q_1} + {Q_2}} \right)}^2}}}{4} = \dfrac{{{{\left( {{{8.10}^{ - 6}}} \right)}^2}}}{4} = 1,{6.10^{ - 11}}\end{array}$

Và $\left| {cos\Delta \varphi } \right|{\rm{}} \le 1$

Kết hợp (1) ta suy ra: $\omega \ge \dfrac{{{{6.10}^{ - 9}}}}{{1,{{6.10}^{ - 11}}}} = 375rad/s$

Lại có: $f = \dfrac{\omega }{{2\pi }} \to f \ge \dfrac{{375}}{{2\pi }} = 59,683Hz$

Câu 23 :

A.

$72nW$
B.

$72mW$
C.

$72\mu W$
D.

$7200W$

Đáp án : C

Phương pháp giải :

+ Áp dụng công thức tính công suất và công thức tính năng lượng mạch dao động: ${\rm{W}} = \dfrac{1}{2}LI_0^2 = \dfrac{1}{2}CU_0^2$

+ Sử dụng biểu thức tính công suất: $P = {I^2}R$

Lời giải chi tiết :

Nếu mạch dao động luôn có ${U_0} = {\rm{ }}12V$ thì về mặt năng lượng ta có:

${W_{tmax}} = {\rm{ }}{W_{dmax}}$

$\begin{array}{l} \Leftrightarrow \dfrac{1}{2}L.I_0^2 = \dfrac{1}{2}C.U_0^2\\ \Rightarrow {I_0} = \sqrt {\dfrac{{C.U_0^2}}{L}} = \sqrt {\dfrac{{{{5.10}^{ - 6}}{{.12}^2}}}{{{{50.10}^{ - 3}}}}} = {12.10^{ - 2}}A\\ \Rightarrow P = R.{I^2} = R.{\left( {\dfrac{{{I_0}}}{{\sqrt 2 }}} \right)^2} = {72.10^{ - 6}}{\rm{W}}\end{array}$

=> Công suất cần cung cấp cho mạch là: $P = 72\mu {\rm{W}}$

Câu 24 :

A.

$2\Omega $
B.

$0,5\Omega $
C.

$1\Omega $
D.

$0,25\Omega $

Đáp án : C

Phương pháp giải :

+ Sử dụng biểu thức tính chu kì: $T = 2\pi \sqrt {LC} $

+ Sử dụng biểu thức định luật Ôm: $I = \dfrac{E}{r}$
+ Sử dụng định luật bảo toàn năng lượng điện từ ${{\rm{W}}_{LC}} = \dfrac{{LI_0^2}}{2} = \dfrac{{CU_0^2}}{2}$

Lời giải chi tiết :

+ Ta có: $T = 2\pi \sqrt {LC} {\rm{}}$

=> Độ tự cảm của cuộn dây: $L = \dfrac{{{T^2}}}{{4{\pi ^2}C}} = \dfrac{{{{\left( {\pi {{.10}^{ - 6}}} \right)}^2}}}{{4{\pi ^2}.2,{{5.10}^{ - 7}}}} = {10^{ - 6}}H$

+ Cường độ dòng điện cực đại chạy qua cuộn dây: ${I_0} = \dfrac{E}{r}$

+ Hiệu điện thế cực đại trên tụ: ${U_{0}} = {\rm{ }}2E$

+ Ta có: $i = 0,04c{\rm{os}}{2.10^7}t(A)$

$\dfrac{{LI_0^2}}{2} = \dfrac{{CU_0^2}}{2} \Leftrightarrow L\dfrac{{{E^2}}}{{{r^2}}} = C.4.{E^2} \Rightarrow r = \sqrt {\dfrac{L}{{4C}}} {\rm{}} = \sqrt {\dfrac{{{{10}^{ - 6}}}}{{{{4.2,5.10}^{ - 7}}}}} {\rm{}} = 1\Omega $

Câu 25 :

A.

${10^{ - 9}}C$
B.

${8.10^{ - 9}}C$
C.

${2.10^{ - 9}}C$
D.

${4.10^{ - 9}}C$

Đáp án : C

Phương pháp giải :

Công thức liên hệ giữa cường độ dòng điện cực đại và điện tích cực đại: ${I_{0}} = {\rm{ }}\omega {Q_0}$

Lời giải chi tiết :

Điện tích cực đại của tụ là : ${Q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{0,04}}{{{{2.10}^7}}} = {2.10^{ - 9}}C$

Câu 26 :

A.

$\dfrac{{{{10}^{ - 6}}}}{3}s$
B.

$\dfrac{{{{2.10}^{ - 6}}}}{3}s$
C.

$\dfrac{{{{10}^{ - 6}}}}{6}s$
D.

$\dfrac{{{{10}^{ - 6}}}}{{12}}s$

Đáp án : B

Phương pháp giải :

+ Sử dụng biểu thức tính tần số góc của mạch dao động LC: $\omega = \dfrac{1}{{\sqrt {LC} }}$

+ Sử dụng đường tròn lượng giác

+ Vận dụng biểu thức: $\Delta \varphi = \omega \Delta t$

Lời giải chi tiết :

Tần số góc của mạch 1 và mạch 2: ${\omega _1} = {\omega _2} = \dfrac{1}{{\sqrt {{L_1}{C_1}} }} = \dfrac{1}{{\sqrt {{{2.10}^{ - 6}}.0,{{2.10}^{ - 6}}} }} = 5\pi {.10^5}(rad/s)$

Phương trình hiệu điện thế của mạch 1 và mạch 2: $\left\{ \begin{array}{l}{u_1} = 8\cos \left( {5\pi {{.10}^5}t} \right)\\{u_2} = 16\cos \left( {5\pi {{.10}^5}t} \right)\end{array} \right. \Rightarrow \Delta u = {u_2} - {u_1} = 8\cos \left( {5\pi {{.10}^5}t} \right)$

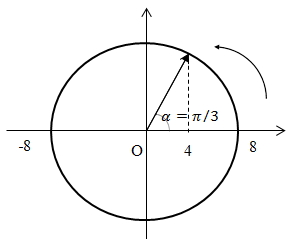
Biểu diễn trên đường tròn lượng giác ta có:

Góc quét được : $\alpha {\rm{}} = \dfrac{{\pi {\rm{}}}}{3} \Rightarrow \Delta t = \dfrac{{\alpha {\rm{}}}}{\omega } = \dfrac{{\pi {\rm{}}}}{{3.5\pi {{.10}^5}}} = \dfrac{{{{2.10}^{ - 6}}}}{3}s$

Câu 27 :

A.

$4V$
B.

$3,6V$
C.

$3\sqrt 2 V$
D.

$3\sqrt 3 V$

Đáp án : D

Phương pháp giải :

Sử dụng công thức tính năng lượng mạch dao động: ${\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = \dfrac{1}{2}L{i^2} + \dfrac{1}{2}C{u^2} = \dfrac{1}{2}CU_0^2$

Lời giải chi tiết :

Áp dụng công thức tính năng lượng mạch dao động ta có:

$\dfrac{1}{2}C{u^2} + \dfrac{1}{2}L{i^2} = \dfrac{1}{2}CU_0^2$

$ \Leftrightarrow \dfrac{1}{2}{.8.10^{ - 9}}.{u^2} + \dfrac{1}{2}{.2.10^{ - 3}}.{({6.10^{ - 3}})^2} = \dfrac{1}{2}{.8.10^{ - 9}}{.6^2}$

$ = > u = 3\sqrt 3 V$

Câu 28 :

A.

$10$
B.

0,1
C.

1000
D.

100

Đáp án : D

Phương pháp giải :

Sử dụng công thức tính bước sóng thu được của mạch dao động điện từ $\lambda = 2\pi c\sqrt {LC} $

Lời giải chi tiết :

Bước sóng điện từ được xác định theo công thức: $\lambda {\rm{}} = cT = c2\pi \sqrt {LC} $

Ta có tỉ số: $\dfrac{{{C_2}}}{{{C_1}}} = \dfrac{{\lambda _2^2}}{{\lambda _1^2}} = \dfrac{{{{1000}^2}}}{{{{100}^2}}} = 100$

Câu 29 :

A.

$0,33{\rm{ }}\mu s$
B.

$0,25{\rm{ }}\mu s$
C.

$1,00{\rm{ }}\mu s$
D.

$0,50{\rm{ }}\mu s$

Đáp án : B

Phương pháp giải :

+ Sử dụng lí thuyết về pha dao động của cảm ứng từ và điện trường: Tại một thời điểm có sóng điện từ truyền qua, cảm ứng từ và cường độ điện trường biến thiên cùng pha

+ Sử dụng biểu thức tính chu kì: $T = \dfrac{{2\pi }}{\omega }$

+ Sử dụng vòng tròn lượng giác

Lời giải chi tiết :

+ Do cảm ứng từ và cường độ điện trường biến thiên cùng pha, ta suy ra phương trình của cường độ điện trường: $E = {E_0}cos\left( {2\pi {{.10}^6}t} \right)$

+ Chu kì: $T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi {{.10}^6}}} = {10^{ - 6}}s = 1\mu s$

+ Tại thời điểm $t = 0$ cường độ điện trường $E = {E_0}cos0 = {E_0}$

Biểu diễn trên đường tròn lượng giác:

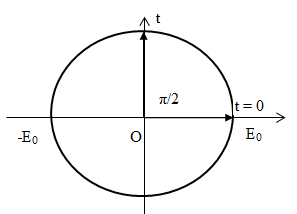
Kể từ lúc $t{\rm{ }} = {\rm{ }}0$, thời điểm đầu tiên cường độ điện trường bằng $0$ là: $t = \dfrac{T}{4} = \dfrac{10^{-6}}{4} = 0,25\mu s$

Câu 30 :

Một mạch dao động LC lí tưởng khi điện áp hai đầu bản tụ $u = 0,8{U_0}$ và tụ đang tích điện thì dòng điện trong mạch:

A.

$\dfrac{{3{U_0}}}{5}\sqrt {\dfrac{C}{L}} $ đang giảm
B.

$\dfrac{{3{U_0}}}{5}\sqrt {\dfrac{C}{L}} $ đang tăng
C.

$\dfrac{{4{U_0}}}{5}\sqrt {\dfrac{C}{L}} $ đang giảm
D.

$\dfrac{{4{U_0}}}{5}\sqrt {\dfrac{C}{L}} $ đang tăng

Đáp án : A

Phương pháp giải :

+ Sử dụng công thức vuông pha giữa u và i trong dao động điện từ tự do: ${\left( {\dfrac{i}{{{I_0}}}} \right)^2} + {\left( {\dfrac{u}{{{U_0}}}} \right)^2} = 1$

+ Cường độ dòng điện nhanh pha hơn hiệu điện thế một góc $\dfrac{\pi }{2}$

Lời giải chi tiết :

Ta có: $\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_0^2}} = 1 \Rightarrow i = {I_0}\sqrt {1 - \frac{{{u^2}}}{{U_0^2}}} {\rm{}} = {U_0}\sqrt {\frac{C}{L}} .\sqrt {1 - {{0,8}^2}} {\rm{}} = \frac{{3{U_0}}}{5}\sqrt {\frac{C}{L}} $

Vì $u{\rm{ }} = {\rm{ }}0,8{U_0}$ và tụ đang tích điện, nghĩa là đang tăng mà $i$ nhanh pha hơn $u$ góc $\dfrac{\pi }{2}$ nên khi đó $i$ đang giảm

Câu 31 :

Cho một mạch đang có dao động điện tử. Nếu cứ sau mỗi chu kì dao động, năng lượng điện tử toàn phần giảm $19\% $ thì biên độ dòng điện giảm?

A.

7%
B.

6%
C.

10%
D.

4%

Đáp án : C

Phương pháp giải :

Vận dụng biểu thức tính năng lượng: ${\rm{W}} = \dfrac{1}{2}LI_0^2$

Lời giải chi tiết :

Ta có: $\dfrac{{\Delta {\rm{W}}}}{{\rm{W}}} = \dfrac{{I_0^2 - {I'^2}}}{{I_0^2}} = \dfrac{{\left( {{I_0} - I'} \right)\left( {{I_0} + I'} \right)}}{{I_0^2}} = \dfrac{{\Delta I}}{{{I_0}}}\dfrac{{\left( {2{I_0} - \Delta I} \right)}}{{{I_0}}} = \dfrac{{\Delta I}}{{{I_0}}}\left( {2 - \dfrac{{\Delta I}}{{{I_0}}}} \right) = 0,19$

Với $x = \dfrac{{\Delta I}}{{{I_0}}}$ ta có ${x^2} - 2x + 0,19 = 0 \to x = 0,1$

=> Biên độ dòng điện giảm $10\% $

Câu 32 :

A.

$i = \dfrac{{{I_0}}}{n}$
B.

$i = \pm \dfrac{{{I_0}}}{{\sqrt {n + 1} }}$
C.

$i = {\rm{ }}{I_0}$
D.

$i = \pm \sqrt {\dfrac{n}{{n + 1}}} {I_0}$

Đáp án : B

Phương pháp giải :

Áp dụng công thức tính năng lượng trong mạch dao động: ${\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = \dfrac{1}{2}C{u^2} + \dfrac{1}{2}L{i^2} = \dfrac{1}{2}LI_0^2 = \dfrac{1}{2}CU_0^2$

Lời giải chi tiết :

Ta có:

$\begin{array}{l}\dfrac{1}{2}.C.{u^2} + \dfrac{1}{2}L.{i^2} = \dfrac{1}{2}.L.I_0^2\\ \Rightarrow (n + 1).L.{i^2} = L.I_0^2\\ \Rightarrow i = \pm \dfrac{{{I_0}}}{{\sqrt {n + 1} }}\end{array}$

Câu 33 :

A.

$175MHz$
B.

$125MHz$
C.

$25MHz$
D.

$87,5MHz$

Đáp án : A

Phương pháp giải :

+ Sử dụng công thức tính tần số của mạch dao động: $f = \dfrac{1}{{2\pi \sqrt {LC} }}$

+ Sử dụng công thức tụ mắc nối tiếp: $\dfrac{1}{{{C_b}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ... + \dfrac{1}{{{C_n}}}$

Lời giải chi tiết :

+ Công thức tính tần số mạch dao động là:$f = \dfrac{1}{{2\pi \sqrt {LC} }}$

+ Công thức tính điện dung của tụ mắc nối tiếp là: $\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$

$\begin{array}{l} \to {f^2} = f_1^2 + f_2^2 = {75^2} + {(50\sqrt {10} )^2}\\ \to f = 175MHz\end{array}$

Câu 34 :

A.

$1,{3.10^{ - 4}}s$
B.

$1,{7.10^{ - 4}}s$
C.

$3,{4.10^{ - 5}}s$
D.

${7.10^{ - 5}}s$

Đáp án : A

Phương pháp giải :

+ Sử dụng công thức tính chu kì: $T = 2\pi \sqrt {LC} $

+ Sử dụng công thức điện dung của tụ mắc song song: ${C_b} = {C_1} + {C_2} + ... + {C_n}$ C

Lời giải chi tiết :

+ Ta có công thức tính chu kì của mạch dao động là: $T = 2\pi \sqrt {LC} $

+ Khi tụ mắc song song với nhau thì công thức tính điện dung tương đương là: $C = {C_1} + {C_2}$

Suy ra công thức tính chu kì của mạch có tụ mắc song song là: ${T^2} = T_1^2 + T_2^2{\rm{ }} = > T = \sqrt {T_1^2 + T_2^2} = 1,{3.10^{ - 4}}s{\rm{ }}$

Câu 35 :

A.

$2,5\pi {.10^{ - 6}}s$
B.

$10\pi {.10^{ - 6}}s$
C.

${10^{ - 6}}s$
D.

$5\pi {.10^{ - 6}}s$

Đáp án : D

Phương pháp giải :

Sử dụng biểu thức tính chu kì: $T = 2\pi \sqrt {LC} $

Lời giải chi tiết :

Cứ sau mỗi nửa chu kì thì $q$ lại có độ lớn cực đại.

Ta có:
$\begin{array}{*{20}{l}}{T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {LC} = 2\pi \sqrt {{{5.10}^{ - 3}}{{.5.10}^{ - 9}}} = \pi {{.10}^{ - 5}}s}\\{ = > \Delta t = \dfrac{T}{2} = 5\pi {{.10}^{ - 6}}s}\end{array}$

Câu 36 :

A.

$T = 2\pi {Q_0}{I_0}$
B.

$T = 2\pi \dfrac{{{I_0}}}{{{Q_0}}}$
C.

$T = 2\pi LC$
D.

$T = 2\pi \dfrac{{{Q_0}}}{{{I_0}}}$

Đáp án : D

Phương pháp giải :

+ Vận dụng biểu thức tính cường độ dòng điện cực đại: ${I_0} = \omega {Q_0}$

+ Sử dụng biểu thức tính chu kì: $T = \dfrac{{2\pi }}{\omega }$

Lời giải chi tiết :

Ta có cường độ dòng điện cực đại trong mạch: ${I_0} = \omega {Q_0}$

Lại có $T = \dfrac{{2\pi }}{\omega }$

=> Chu kỳ dao động điện từ của mạch là: $T = \dfrac{{2\pi }}{\omega } = 2\pi \dfrac{{{Q_0}}}{{{I_0}}}$

Câu 37 :

A.

$\dfrac{T}{6}$
B.

$\dfrac{{2T}}{3}$
C.

$\dfrac{{5T}}{{12}}$
D.

$\dfrac{T}{3}$

Đáp án : B

Phương pháp giải :

+ Sử dụng công thức tính thời gian bằng đường tròn.

+ Sử dụng biểu thức: $\Delta \varphi = \omega \Delta t$

Lời giải chi tiết :

+ Ta có phương trình điện tích : $q = {Q_0}.\cos \left( {\omega t + \varphi } \right)$

+ Ban đầu bản $A$ tích điện $\dfrac{{{Q_0}}}{2}$ và đang tăng nên pha ban đầu có giá trị $\varphi = \dfrac{{ - \pi }}{3}$

+ Khi bản $B$ có điện tích cực đại ${Q_0}$ thì bản $A$ có điện tích $-{Q_0}$ .

Ta có vecto quay như hình vẽ:

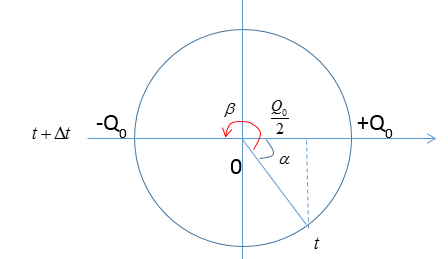
Ta có:

$\begin{array}{l}cos\alpha = \dfrac{{\dfrac{{{Q_0}}}{2}}}{{{Q_0}}} = \dfrac{1}{2} \to \alpha = \dfrac{\pi }{3}\\ \to \beta = \pi + \dfrac{\pi }{3} = \dfrac{{4\pi }}{3}\end{array}$

Mặt khác, ta có:

$\begin{array}{l}\beta = \omega \Delta t = \dfrac{{2\pi }}{T}\Delta t\\ \to \Delta t = \dfrac{\beta }{{2\pi }}T = \dfrac{{\dfrac{{4\pi }}{3}}}{{2\pi }}T = \dfrac{2}{3}T\end{array}$

Câu 38 :

A.

$i = 2\cos ({5.10^5}t - \dfrac{\pi }{3})A$
B.

$i = 2\cos ({5.10^5}t - \dfrac{{2\pi }}{3})A$
C.

$i = 2\cos ({5.10^5}t + \dfrac{{2\pi }}{3})A$
D.

$i = 2\cos ({5.10^5}t + \dfrac{\pi }{3})A$

Đáp án : A

Phương pháp giải :

+ Vận dụng biểu thức: $i = q'$

+ Sử dụng vòng tròn lượng giác

+ Sử dụng biểu thức tính tần số góc: $\omega = \dfrac{1}{{\sqrt {LC} }}$

+ Sử dụng công thức tính năng lượng mạch dao động: ${\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = \dfrac{1}{2}L{i^2} + \dfrac{1}{2}C{u^2} = \dfrac{1}{2}CU_0^2$

+ Viết phương trình cường độ dòng điện trong mạch.

Lời giải chi tiết :

+ Giả sử phương trình điện tích là : $q = {Q_0}.\cos \left( {\omega t + \varphi } \right)$

+ Phương trình cường độ dòng điện là : $i = q' = - \omega .{Q_0}.\sin \left( {\omega t + \varphi } \right) = {I_0}.\cos \left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)$

Tụ đang phóng điện tức là $q$ đang giảm

Vì q đang giảm nên I đang tăng => Lấy vị trí thứ (2)

=> Ta có phương trình của i là : $i = {I_0}.\cos \left( {\omega t - \dfrac{\pi }{3}} \right)$

Với tần số góc: $\omega = \dfrac{1}{{\sqrt {LC} }} = {5.10^5}rad/s$

Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì năng lượng từ trường cũng bằng một nửa năng lượng từ trường cực đại nên :

$\begin{array}{*{20}{l}}{\dfrac{1}{2}L{i^2} = \dfrac{1}{2}.\dfrac{1}{2}LI_0^2}\\\begin{array}{l} \to I_0^2 = 2{i^2} = 2{\left( {\sqrt 2 } \right)^2} = 4\\ \to {I_0} = 2A\end{array}\end{array}$

Vậy phương trình của dòng điện I là: $i = 2.\cos \left( {{{5.10}^5}t - \dfrac{\pi }{3}} \right)A$

Câu 39 :

A.

${120^0}$
B.

${150^0}$
C.

${60^0}$
D.

${30^0}$

Đáp án : B

Phương pháp giải :

+ Vận dụng biểu thức hàm bậc nhất của tụ điện: $C = a\alpha + b$

+ Vận dụng biểu thức tính bước sóng: $\lambda = 2\pi c\sqrt {LC} $

Lời giải chi tiết :

+ Điện dung của tụ phụ thuộc góc quay của bản tụ: $C = a\alpha + b$

+ Với hai giá trị lớn nhất và nhỏ nhất của điện dụng là ${C_1}$ và ${C_2}$, ta có:

$\left\{ {\begin{array}{*{20}{l}}{a.0 + b = 10(pF)}\\{a.180 + b = 370(pF)}\end{array}} \right. \to \left\{ {\begin{array}{*{20}{l}}{a = 2(pF)}\\{b = 10(pF)}\end{array}} \right. \to C = 2.\alpha {\rm{}} + 10(pF)(1)$

+ Để bắt được sóng có bước sóng $\lambda {\rm{ }} = {\rm{ }}22,3{\rm{ }}m$ thì điện dung của tụ bằng $C = \dfrac{{{\lambda ^2}}}{{4{\pi ^2}{c^2}L}} = {70.10^{ - 12}}(F) = 70(pF)$

Thay vào (1) tìm được $\alpha {\rm{ }} = {\rm{ }}{30^0}$

Vậy phải tụ phải quay một góc bằng ${150^0}$ từ vị trí có điện dung cực đại (ứng với góc ${180^0}$)

Câu 40 :

A.

$\dfrac{{\sqrt 3 {I_0}}}{{2\omega }}$
B.

$\dfrac{{{I_0}}}{{2\omega }}$
C.

$\dfrac{{\sqrt 3 {I_0}\omega }}{2}$
D.

$\dfrac{{{I_0}\omega }}{2}$

Đáp án : A

Phương pháp giải :

+ Sử dụng vecto quay tính thời gian dòng điện chạy qua dây dẫn

+ Sử dụng công thưc tính điện lượng và cường độ dòng điện: $\left\{ \begin{array}{l}q\\i = q'\end{array} \right.$

Cường độ dòng điện nhanh pha hơn điện tích một góc $\dfrac{\pi }{2}$

Lời giải chi tiết :

+ Cường độ dòng điện trong mạch $LC$ sớm pha $\dfrac{\pi }{2}$ so với điện lượng.

+ Nên khi ban đầu cường độ dòng điện cực đại thì điện lượng bằng $0$, cường độ dòng điện đang giảm thì $q$ đang tăng.

$\begin{array}{l}i = \dfrac{{{I_0}}}{2} \Rightarrow {\varphi _i} = \dfrac{\pi }{3} \Rightarrow {\varphi _q} = \dfrac{\pi }{3} - \dfrac{\pi }{2} = \dfrac{{ - \pi }}{6}\\ \Rightarrow q = \dfrac{{{I_0}}}{\omega }.\cos \left( {\dfrac{{ - \pi }}{6}} \right) = \dfrac{{\sqrt 3 }}{2}\dfrac{{{I_0}}}{\omega }\\ \Rightarrow \Delta q = q - 0 = \dfrac{{\sqrt 3 }}{2}\dfrac{{{I_0}}}{\omega }\end{array}$

Câu 41 :

A.

$\dfrac{{250}}{3}ns$
B.

$62,5{\rm{ }}ns$
C.

$\dfrac{{500}}{3}ns$
D.

$125{\rm{ }}ns$

Đáp án : D

Phương pháp giải :

+ Áp dụng vòng tròn lượng giác trong dao đông điện từ

+ Vận dụng biểu thức tính bước sóng: $\lambda = cT$

Lời giải chi tiết :

Theo bài ra ta có tại thời điểm t: $E = \dfrac{{{E_0}\sqrt 3 }}{3} = > B = \dfrac{{{B_0}\sqrt 3 }}{3}$ ( đang tăng)

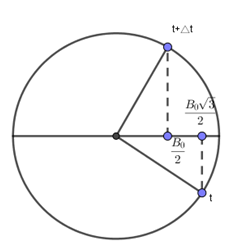
$T = \dfrac{\lambda }{c} = \dfrac{{150}}{{{{3.10}^8}}} = {5.10^{ - 7}}s$

Thời gian ngắn nhất cảm ứng từ tại điểm đó có giá trị bằng $\dfrac{{{B_0}}}{2}$là:

$\Delta t = \dfrac{T}{{12}} + \dfrac{T}{6} = \dfrac{T}{4} = \dfrac{{{{5.10}^{ - 7}}}}{4} = 1,{25.10^{ - 7}}s = 125ns$

Câu 42 :

Trong nguyên tắc thông tin liên lạc bằng sóng vô tuyến, biến điệu sóng là:

A.

biến dao động âm thành dao động điện âm tần.
B.

làm cho biên độ sóng giảm xuống.
C.

trộn sóng âm tần với sóng cao tần.
D.

tách sóng âm tần ra khỏi sóng cao tần.

Đáp án : C

Phương pháp giải :

Sử dụng lí thuyết về nguyên tắc thông tin liên lạc bằng sóng vô tuyến

Lời giải chi tiết :

Trong truyền thông bằng sóng điện từ thì biến điệu sóng là trộn sóng âm tần với sóng cao tần.

Câu 43 :

A.

$q{\rm{ }} = {\rm{ }}0,2cos\left( {{{2.10}^6}t{\rm{ }}} \right)\left( {nC} \right)$
B.

$q{\rm{ }} = {\rm{ }}0,2cos\left( {{{2.10}^6}t} \right)\left( {\mu C} \right)$
C.

$q{\rm{ }} = {\rm{ }}0,2cos\left( {{{2.10}^6}t{\rm{ }} - {\rm{ }}\pi } \right)\left( {\mu C} \right)$
D.

$q{\rm{ }} = {\rm{ }}0,2cos\left( {{{2.10}^6}1{\rm{ }} - \pi } \right)\left( {nC} \right)$

Đáp án : C

Phương pháp giải :

Vận dụng biểu thức xác định cường độ dòng điện: $i = q'$

Lời giải chi tiết :

Ta có:

$\begin{array}{l}i = q' \to q = \int\limits_0^t {idt = \int\limits_0^t {0,4\cos \left( {{{2.10}^6}t - \dfrac{\pi }{2}} \right)dt} } \\ = \dfrac{{0,4}}{{{{2.10}^{ - 6}}}}.\sin \left( {{{2.10}^6}t - \dfrac{\pi }{2}} \right)\left| \begin{array}{l}t\\0\end{array} \right.\\ = 0,2\cos \left( {{{2.10}^{ - 6}}t - \pi } \right)\mu C\end{array}$

Câu 44 :

A.
Sóng dài
B.
Sóng cực ngắn
C.
Sóng trung
D.
Sóng ngắn

Đáp án : D

Phương pháp giải :

+ Vận dụng biểu thức liên hệ giữa cường độ dòng điện cực đại và điện tích cực đại: $I_0=\omega Q_0$

+ Sử dụng biểu thức: $\omega=2\pi f$

+ Áp dụng công thức tính bước sóng sóng điện từ $\lambda = \dfrac{c}{f} = 2\pi c .\dfrac{{{Q_0}}}{{{I_0}}}$

+ Sử dụng thang sóng vô tuyến

Lời giải chi tiết :

Ta có,

$I_0=\omega Q_0$

=> $\omega = \dfrac{I_0}{Q_0}$

Lại có: $\omega=2\pi f=> f=\dfrac{\omega}{2\pi}=\dfrac{I_0}{2\pi Q_0}$

+ Bước sóng mà mạch dao động phát ra là $\lambda = \dfrac{c}{f} = 2\pi c \dfrac{{{Q_0}}}{{{I_0}}} = 2\pi {3.10^8}\dfrac{{{{2.10}^{ - 9}}}}{{0,3}} = 12,56m$ thuộc vùng sóng ngắn

Trắc nghiệm Tổng hợp bài tập năng lượng dao động điện từ (phần 2) - Vật Lí 12

Luyện tập và củng cố kiến thức Tổng hợp bài tập năng lượng dao động điện từ (phần 2) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Tổng hợp bài tập dao động và sóng điện từ (phần 1) - Vật Lí 12

Luyện tập và củng cố kiến thức Tổng hợp bài tập dao động và sóng điện từ (phần 1) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 23. Nguyên tắc thông tin liên lạc bằng sóng vô tuyến - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 23. Nguyên tắc thông tin liên lạc bằng sóng vô tuyến Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 22. Sóng điện từ - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 22. Sóng điện từ Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 21. Điện từ trường - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 21. Điện từ trường Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 20. Phương trình dao động mạch LC (q - u - i) - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 20. Phương trình dao động mạch LC (q - u - i) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 20. Các loại dao động - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 20. Các loại dao động Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 20. Bài tập năng lượng của mạch dao dộng LC - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 20. Bài tập năng lượng của mạch dao dộng LC Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 20. Bài tập mạch dao động LC - Các đại lượng đặc trưng - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 20. Bài tập mạch dao động LC - Các đại lượng đặc trưng Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Bài giải mới nhất

Trắc nghiệm Ôn tập chương 4 - Vật Lí 12

Báo lỗi góp ý