Bài tập trắc nghiệm Lí 12 có đáp án Bài tập trắc nghiệm Chương 2. Sóng cơ và sóng âm

Trắc nghiệm Bài 7. Phương trình sóng cơ học - Vật Lí 12

Làm bài tập

Đề bài

Câu 1 :

Sóng truyền từ $O$ đến $M$ với vận tốc $v = 40cm/s$, phương trình sóng tại $O$ là ${u_0} = 4sin\dfrac{\pi }{2}t\left( {cm} \right)$. Biết vào thời điểm $t$ thì li độ của phần tử $M$ là $3cm$ và đang chuyển động theo chiều dương, vậy lúc $t + 6(s)$ li độ của $M$ là:

A.

$-3 cm$
B.

$-2 cm$
C.

$ 2 cm$
D.

$3 cm$

Câu 2 :

Một sóng cơ lan truyền trên một sợi dây rất dài có phương trình $u = 6\cos \left( {4\pi t - 0,02\pi x} \right)$; trong đó u và x có đơn vị là cm, t có đơn vị là giây. Hãy xác định li độ dao động của một điểm trên dây có toạ độ x = 25 cm tại thời điểm t = 4 s.

A.

0 cm
B.

6 cm
C.

3 cm
D.

-6 cm

Câu 3 :

Một sóng cơ học lan truyền trên mặt nước với tốc độ 25cm/s. Phương trình sóng tại nguồn là u = 3cosπt(cm). Vận tốc của phần tử vật chất tại điểm M cách O một khoảng 25cm tại thời điểm t = 2,5s là:

A.

25cm/s
B.

3π cm/s.
C.

0 cm/s
D.

-3π cm/s.

Câu 4 :

Nguồn sóng ở O dao động với tần số 10Hz, dao động truyền đi với vận tốc 0,4m/s theo phương Oy; trên phương này có hai điểm P và Q với PQ = 15cm. Biên độ sóng bằng a = 1cm và không thay đổi khi lan truyền . Nếu tại thời điểm t nào đó P có li độ 1cm thì li độ tại Q là:

A.

1cm
B.

-1cm
C.

0 cm
D.

2cm

Câu 5 :

Sóng có tần số $20Hz$ truyền trên chất lỏng với tốc độ $200cm/s$, gây ra các dao động theo phương thẳng đứng của các phần tử chất lỏng. Hai điểm M và N thuộc mặt chất lỏng cùng phương truyền sóng cách nhau $22,5cm$. Biết điểm M nằm gần nguồn sóng hơn. Tại thời điểm t điểm N hạ xuống thấp nhất. Hỏi sau đó thời gian ngắn nhất là bao nhiêu thì điểm M sẽ hạ xuống thấp nhất?

A.

$\dfrac{3}{{20}}(s)$
B.

$\dfrac{3}{{80}}(s)$
C.

$\dfrac{7}{{160}}(s)$
D.

$\dfrac{1}{{160}}(s)$

Câu 6 :

Sóng truyền theo phương ngang trên một sợi dây dài với tần số $10Hz$. Điểm $M$ trên dây tại một thời điểm đang ở vị trí cao nhất và tại thời điểm đó điểm $N$ cách $M$ $5cm$ đang đi qua vị trí có li độ bằng nửa biên độ và đi lên. Coi biên độ sóng không đổi khi truyền. Biết khoảng cách $MN$ nhỏ hơn bước sóng của sóng trên dây. Chọn đáp án đúng cho tốc độ truyền sóng và chiều truyền sóng.

A.

$60cm/s$, truyền từ $M$ đến $N$
B.

$3m/s$, truyền từ $N$ đến $M$
C.

$60cm/s$, từ $N$ đến $M$
D.

$30cm/s$, từ $M$ đến $N$

Câu 7 :

Hai điểm M, N cùng nằm trên một phương truyền sóng cách nhau λ/3. Tại thời điểm t, khi li độ dao động tại M là u_M = + 3 cm thì li độ dao động tại N là u_N = - 3 cm. Biên độ sóng bằng :

A.

$A = \sqrt 6 cm$
B.

A = 3 cm.
C.

$A = 2\sqrt 3 cm$
D.

$A = 3\sqrt 3 cm$.

Câu 8 :

Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình sóng tại nguồn O là:

${u_O} = A\sin (\frac{{2\pi }}{T}t)(cm).$ Một điểm M cách nguồn O bằng $\frac{1}{3}$ bước sóng ở thời điểm $t = \frac{T}{2}$ có ly độ ${u_M} = 2(cm).$ Biên độ sóng A là:

A.

$4/\sqrt 3 (cm).$
B.

$2\sqrt 3 (cm).$
C.

2(cm)
D.

4(cm)

Câu 9 :

Một sóng cơ lan truyền từ nguồn O, dọc theo trục Ox với biên độ sóng không đổi, chu kì sóng T và bước sóng $\lambda $. Biết rằng tại thời điểm t = 0, phần tử tại O qua vị trí cân bằng theo chiều dương và tại thời điểm t = $\frac{{5T}}{6}$ phần tử tại điểm M cách O một đoạn d = $\frac{\lambda }{6}$ có li độ là -2 cm. Biên độ sóng là :

A.

4/$\sqrt 3 $ cm
B.

2$\sqrt 2 $
C.

2$\sqrt 3 $ cm
D.

4 cm

Câu 10 :

Trên một sợi dây dài vô hạn có một sóng cơ lan truyền theo phương Ox với phương trình sóng u = 2cos(10πt - πx) (cm) ( trong đó t tính bằng s; x tính bằng m). M, N là hai điểm nằm cùng phía so với O cách nhau 5 m. Tại cùng một thời điểm khi phần tử M đi qua vị trí cân bằng theo chiều dương thì phần tử N

A.

Đi qua vị trí cân bằng theo chiều dương
B.

Đi qua vị trí cân bằng theo chiều âm
C.

Ở vị trí biên dương
D.

Ở vị trí biên âm

Câu 11 :

Cho phương trình sóng: $u = a\sin \left( {0,4\pi x + 7\pi t + \dfrac{\pi }{3}} \right)\left( {m,s} \right)$. Phương trình này biểu diễn:

A.

Sóng chạy theo chiều âm của trục x với vận tốc $\dfrac{{10}}{7}$ (m/s)
B.

Sóng chạy theo chiều dương của trục x với vận tốc $\dfrac{{10}}{7}$ cm/s
C.

Sóng chạy theo chiều dương của trục x với vận tốc $17,5 (m/s)$
D.

Sóng chạy theo chiều âm của trục x với vận tốc $17,5 (m/s)$

Câu 12 :

Một nguồn O dao động với tần số f = 50Hz tạo ra sóng trên mặt nước có biên độ 3cm (coi như không đổi khi sóng truyền đi). Chọn t = 0 là lúc phần tử nước tại O đi qua vị trí cân bằng theo chiều dương. Tại thời điểm t₁ li độ dao động tại M bằng 2cm. Li độ dao động tại M vào thời điểm t₂ = (t₁ + 2,01)s bằng bao nhiêu ?

A.

2cm
B.

-2cm
C.

0cm
D.

-1,5cm

Câu 13 :

Một sóng cơ lan truyền trên một sợi dây rất dài với biên độ không đổi, ba điểm A, B và C nằm trên sợi dây sao cho B là trung điểm của AC. Tại thời điểm t₁, li độ của ba phần tử A, B, C lần lượt là – 4,8mm; 0 mm; 4,8 mm. Nếu tại thời điểm t₂, li độ của A và C đều bằng +5,5 mm, thì li độ của phần tử tại B là:

A.

10,3mm
B.

11,1mm
C.

5,15mm
D.

7,3mm

Câu 14 :

Một sợi dây đàn hồi nằm ngang có điểm đầu O dao động theo phương thẳng đứng với biên độ A = 5cm, T = 0,5s. Vận tốc truyền sóng là 40cm/s. Viết phương trình sóng tại M cách O d = 50 cm.

A.

${u_M} = 5\cos (4\pi t - 5\pi )(cm)$
B.

${u_M} = 5\cos (4\pi t - 2,5\pi )(cm)$
C.

${u_M} = 5\cos (4\pi t + \pi )(cm)$
D.

${u_M} = 5\cos (4\pi t - 25\pi )(cm)$

Câu 15 :

Một sóng cơ học truyền theo phương $Ox$ với biên độ coi như không đổi. Tại $O$, dao động có dạng $u = acosωt (cm)$. Điểm M cách xa tâm dao động O là $\dfrac{1}{3}$ bước sóng ở thời điểm bằng $0,5$ chu kì thì ly độ sóng có giá trị là $5 cm$. Phương trình dao động ở M thỏa mãn hệ thức nào sau đây:

A.

${u_M} = 5\cos (\omega t - \frac{{2\lambda }}{3})cm$
B.

${u_M} = 10\cos (\omega t - \frac{{\pi \lambda }}{3})cm$
C.

${u_M} = 10\cos (\omega t - \frac{{2\pi }}{3})cm$
D.

${u_M} = 5\cos (\omega t - \frac{\pi }{3})cm$

Câu 16 :

Một dao động lan truyền trong môi trường từ điểm $N$ đến điểm $M$ cách $N$ một đoạn $0,9 (m)$ với vận tốc $1,2 (m/s)$. Biết phương trình sóng tại $N$ có dạng $u_N = 0,02cos 2πt(m)$. Viết biểu thức sóng tại $M$ :

A.

$u_M= 0,02cos2πt (m)$
B.

$u_M= 0,02cos(2πt + 3π/2) (m)$
C.

$u_M= 0,02cos(2πt - 3π/2) (m)$
D.

$u_M= 0,02cos(2πt - π) (m)$

Câu 17 :

Một sóng cơ học lan truyền trên một phương truyền sóng với vận tốc $5m/s$. Phương trình sóng của một điểm O trên phương truyền đó là:${u_O} = 6c{\rm{os}}\left( {5\pi t + \dfrac{\pi }{2}} \right)$. Phương trình sóng tại M nằm trước O và cách O một khoảng $50cm$ là:

A.

${u_M} = 6\cos (5\pi t)cm$
B.

${u_M} = 6c{\rm{os}}\left( {5\pi t + \frac{\pi }{2}} \right)$ cm
C.

${u_M} = 6c{\rm{os}}\left( {5\pi t - \frac{\pi }{2}} \right)$ cm
D.

${u_M} = 6\cos (5\pi t + \pi )cm$

Câu 18 :

Sóng truyền từ điểm M đến điểm O rồi đến điểm N trên cùng một phương truyền sóng với tốc độ $v = 20m/s$. Cho biết tại O dao động có phương trình ${u_O} = 4cos\left( {2\pi f - \dfrac{\pi }{2}} \right)cm$ và tại hai điểm gần nhau nhất cách nhau $6m$ trên cùng phương truyền sóng thì dao động lệch pha nhau góc $\dfrac{{2\pi }}{3}rad$. Cho $ON = 50cm$. Phương trình sóng tại N là

A.
${u_N} = 4cos\left( {\dfrac{{40\pi t}}{9} + \dfrac{{5\pi }}{9}} \right)cm.$
B.
${u_N} = 4cos\left( {\dfrac{{40\pi t}}{9} - \dfrac{{5\pi }}{9}} \right)cm.$
C.
${u_N} = 4cos\left( {\dfrac{{20\pi t}}{9} - \dfrac{{5\pi }}{9}} \right)cm$
D.
${u_N} = 4cos\left( {\dfrac{{20\pi t}}{9} + \dfrac{{5\pi }}{9}} \right)cm.$

Câu 19 :

Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình dao động tại nguồn O là ${u_O} = A.\cos \left( {\dfrac{{2\pi t}}{T}} \right)cm$. Một điểm M trên đường thẳng, cách O một khoảng bằng $\dfrac{1}{3}$ bước sóng ở thời điểm $t = \dfrac{T}{2}$ có li độ u_M = 2cm. Biên độ sóng A bằng:

A.
$2\sqrt 3 cm$.
B.
2cm.
C.
4cm.
D.
$\dfrac{{4\sqrt 3 }}{3}cm$

Lời giải và đáp án

Câu 1 :

A.

$-3 cm$
B.

$-2 cm$
C.

$ 2 cm$
D.

$3 cm$

Đáp án : A

Phương pháp giải :

+ Áp dụng công thức tính góc quét: $\Delta \varphi = \omega \Delta t$

+ Sử dụng vòng tròn lượng giác

Lời giải chi tiết :

Góc quét được:

$\Delta \varphi = \omega \Delta t = \dfrac{\pi }{2}6= {3\pi }$

Vẽ trên vòng tròn lượng giác, ta được:

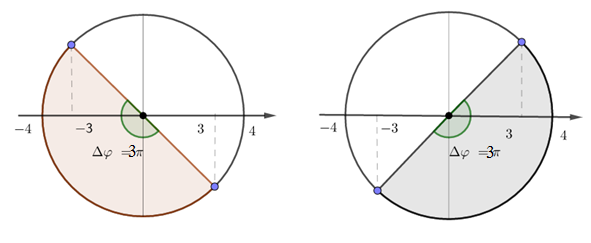
Từ vòng tròn lượng giác, ta có: $t + 6s$ điểm $M$ có li độ $-3cm$

Câu 2 :

A.

0 cm
B.

6 cm
C.

3 cm
D.

-6 cm

Đáp án : A

Phương pháp giải :

Thay x và t vào phương trình dao động

Lời giải chi tiết :

Ta có: $u = 6\cos \left( {4\pi t - 0,02\pi x} \right)$

Thay x = 25cm và t = 4s vào, ta được:

$u = 6\cos \left( {4\pi .4 - 0,02\pi .25} \right) = 0cm$

Câu 3 :

A.

25cm/s
B.

3π cm/s.
C.

0 cm/s
D.

-3π cm/s.

Đáp án : B

Phương pháp giải :

+ Áp dụng công thức tính bước sóng: $\lambda = \frac{v}{f}$

+ Viết phương trình li độ dao động tại M

+ Viết phương trình vận tốc tại M, thay t vào phương trình vận tốc

Lời giải chi tiết :

Ta có: $\lambda = \frac{v}{f} = \frac{{25}}{{\frac{\pi }{{2\pi }}}} = 50cm$

Phương trình dao động tại M cách O một khoảng x = 25cm:

${u_M} = 3c{\rm{os}}\left( {\pi t - \frac{{2\pi x}}{\lambda }} \right) = 3c{\rm{os}}\left( {\pi t - \frac{{2\pi 25}}{{50}}} \right) = 3c{\rm{os}}\left( {\pi t - \pi } \right)cm$

Phương trình vận tốc tại M:

${v_M} = {u_M}' = - 3\pi \sin \left( {\pi t - \pi } \right)cm/s$

=> Vận tốc tại M tại thời điểm t = 2,5s:

${v_M} = - 3\pi \sin \left( {\pi .2,5 - \pi } \right) = 3\pi cm/s$

Câu 4 :

A.

1cm
B.

-1cm
C.

0 cm
D.

2cm

Đáp án : C

Phương pháp giải :

+ Áp dụng công thức tính bước sóng: $\lambda = \frac{v}{f}$

+ Vận dụng công thức tính độ lệch pha: $\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda }$

+ Sử dụng vòng tròn lượng giác.

Lời giải chi tiết :

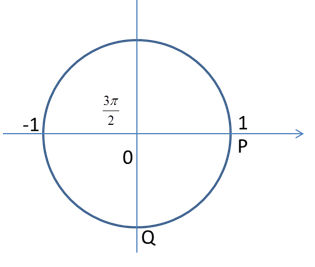
Ta có:

$\lambda = \frac{v}{f} = \frac{{0,4}}{{10}} = 0,04m = 4cm$

Độ lệch pha giữa hai điểm P và Q là:

$\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda } = \frac{{2\pi 15}}{4} = \frac{{15\pi }}{2} = 6\pi + \frac{{3\pi }}{2}$

Từ vòng tròn lượng giác, ta có li độ tại Q là 0cm

Câu 5 :

A.

$\dfrac{3}{{20}}(s)$
B.

$\dfrac{3}{{80}}(s)$
C.

$\dfrac{7}{{160}}(s)$
D.

$\dfrac{1}{{160}}(s)$

Đáp án : B

Phương pháp giải :

+ Áp dụng công thức tính bước sóng: $\lambda = \dfrac{v}{f}$

+ Áp dụng công thức tính chu kì: $T = \dfrac{1}{f} = 0,05{\rm{s}}$

+ Vận dụng công thức tính độ lệch pha: $\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda }$

+ Sử dụng vòng tròn lượng giác.

Lời giải chi tiết :

Ta có:

$\lambda = \dfrac{v}{f} = \dfrac{{200}}{{20}} = 10cm$

Chu kì:

$T = \dfrac{1}{f} = 0,05{\rm{s}}$

Độ lệch pha giữa hai điểm M và N là:

$\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{2\pi 22,5}}{{10}} = \dfrac{{9\pi }}{2} = 4\pi + \dfrac{\pi }{2}$

=> M và N dao động vuông pha nhau

Vì M gần nguồn sóng hơn => M nhanh pha hơn N 1 góc π/2

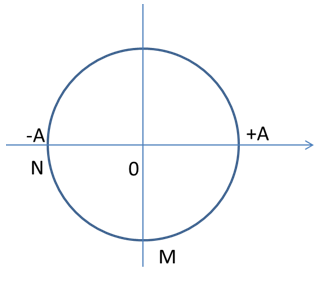
Tại thời điểm t: N đang ở biên âm, M đang ở VTCB theo chiều dương

=> Thời gian ngắn nhất điểm M hạ xuống thấp nhất là: $t = \dfrac{{3T}}{4} = \dfrac{3}{{80}}s$

Câu 6 :

A.

$60cm/s$, truyền từ $M$ đến $N$
B.

$3m/s$, truyền từ $N$ đến $M$
C.

$60cm/s$, từ $N$ đến $M$
D.

$30cm/s$, từ $M$ đến $N$

Đáp án : C

Phương pháp giải :

+ Sử dụng vòng tròn lượng giác.

+ Vận dụng công thức tính độ lệch pha: $\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda }$

+ Áp dụng công thức tính tốc độ truyền sóng: $v = \lambda f$

Lời giải chi tiết :

Ta có:

+ Điểm $M$ ở vị trí cao nhất tức là biên dương.

+ Điểm $N$ qua vị trí có li độ bằng $\dfrac{A}{2}$ và đang đi lên

Vẽ trên vòng tròn lượng giác, ta được:

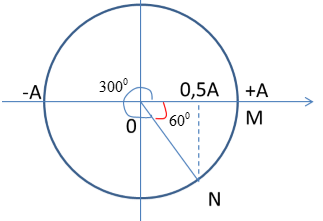
Ta có 2 trường hợp của góc lệch pha giữa $M$ và $N$:

+ TH 1: $M, N$ lệch pha nhau: $60^0$:

$\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{\pi }{3} \to \lambda = 6\Delta d = 6.5 = 30cm\\ \to v = \lambda f = 30.10 = 300cm/s = 3m/s\end{array}$

$M$ sớm pha hơn $N$ => Sóng truyền từ $M$ đến $N$

+ TH 2: $M, N$ lệch pha nhau $300^0$:

$\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{5\pi }}{3} \to \lambda = \dfrac{6}{5}\Delta d = \dfrac{6}{5}.5 = 6cm\\ \to v = \lambda f = 6.10 = 60cm/s\end{array}$

Do $N$ sớm pha hơn $M$

=> Sóng truyền từ $N$ đến $M$

Câu 7 :

A.

$A = \sqrt 6 cm$
B.

A = 3 cm.
C.

$A = 2\sqrt 3 cm$
D.

$A = 3\sqrt 3 cm$.

Đáp án : C

Phương pháp giải :

Áp dụng biểu thức xác định độ lệch pha: $\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda }$

+ Cách 1: Dùng phương trình sóng

Viết phương trình sóng tại M và N

Áp dụng công thức lượng giác: ${\rm{cosa + cosb}} = 2c{\rm{os}}\frac{{a + b}}{2}{\rm{cos}}\frac{{a - b}}{2}$

+ Cách 2: Sử dụng vòng tròn lượng giác

Lời giải chi tiết :

Ta có: Độ lệch pha giữa hai điểm MN là: $\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda } = \frac{{2\pi \frac{\lambda }{3}}}{\lambda } = \frac{{2\pi }}{3}$

Giả sử dao động tại M sớm pha hơn dao động tại N.

Cách 1: Dùng phương trình sóng

Ta có thể viết:

$\begin{array}{l}{u_M} = Ac{\rm{os}}\omega t = + 3cm{\rm{ (1)}}\\{u_N} = Ac{\rm{os}}\left( {\omega t - \frac{{2\pi }}{3}} \right) = - 3cm{\rm{ (2)}}\end{array}$

Lấy (1) + (2), ta được:

$\begin{array}{l}{u_M} + {u_N} = 0 = Ac{\rm{os}}\omega t + Ac{\rm{os}}\left( {\omega t - \frac{{2\pi }}{3}} \right)\\ \leftrightarrow 2Ac{\rm{os}}\frac{\pi }{3}{\rm{cos}}\left( {\omega t - \frac{\pi }{3}} \right) = 0 \to \omega t - \frac{\pi }{3} = \frac{\pi }{2} + k\pi \\ \to \omega t = \frac{{5\pi }}{6} + k\pi \end{array}$

Thay vào (1), ta được:

$Ac{\rm{os}}\left( {\frac{{5\pi }}{6} + k\pi } \right) = 3$

Do A > 0,

$Ac{\rm{os}}\left( {\frac{{5\pi }}{6} - \pi } \right) = 3 \to Ac{\rm{os}}\left( { - \frac{\pi }{6}} \right) = 3 \to A = 2\sqrt 3 cm$

=> Chọn C

Cách 2: Sử dụng vòng tròn lượng giác

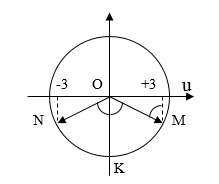
Xác định tọa độ N, M trên vòng tròn lượng giác, ta được:

Từ vòng tròn lượng giác, ta có:

$\begin{array}{l}\angle NOK = \angle KOM = \frac{{\Delta \varphi }}{2} = \frac{\pi }{3}\\ \to {\rm{A}}\sin \frac{\pi }{3} = 3cm \to A = 2\sqrt 3 cm\end{array}$

Câu 8 :

Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình sóng tại nguồn O là:

A.

$4/\sqrt 3 (cm).$
B.

$2\sqrt 3 (cm).$
C.

2(cm)
D.

4(cm)

Đáp án : A

Phương pháp giải :

Áp dụng biểu thức xác định độ lệch pha: $\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda }$

+ Viết phương trình sóng tại M

+ Thay x và t vào phương trình sóng

Lời giải chi tiết :

Ta có:

${u_O} = A\sin (\frac{{2\pi }}{T}t)(cm) \to {u_M}{\rm{ = Asin}}\left( {\frac{{2\pi }}{T}t - \frac{{2\pi x}}{\lambda }} \right)$

Thay t = T/2 và x = λ/3 vào phương trình dao động tại M, ta được:

$\begin{array}{l}{u_M}{\rm{ = Asin}}\left( {\frac{{2\pi }}{T}t - \frac{{2\pi x}}{\lambda }} \right) \leftrightarrow {\rm{Asin}}\left( {\frac{{2\pi }}{T}\frac{T}{2} - \frac{{2\pi \frac{\lambda }{3}}}{\lambda }} \right) = 2\\ \to A\sin \left( {\frac{\pi }{3}} \right) = 2 \to A = \frac{4}{{\sqrt 3 }}cm\end{array}$

Câu 9 :

A.

4/$\sqrt 3 $ cm
B.

2$\sqrt 2 $
C.

2$\sqrt 3 $ cm
D.

4 cm

Đáp án : A

Phương pháp giải :

+ Viết phương trình sóng tại O

+ Viết phương trình sóng tại M

+ Thay x và t vào phương trình sóng

Lời giải chi tiết :

Ta có:

- Phương trình sóng tại O:

${u_0} = Ac{\rm{os}}\left( {\omega t - \frac{\pi }{2}} \right)cm$

- Phương trình sóng tại M:

${u_M} = Ac{\rm{os}}\left( {\omega t - \frac{\pi }{2} - \frac{{2\pi d}}{\lambda }} \right)cm$

Tại t = 5T/6 và d = λ/6

$\begin{array}{l}{u_M} = Ac{\rm{os}}\left( {\frac{{2\pi }}{T}\frac{{5T}}{6} - \frac{\pi }{2} - \frac{{2\pi \frac{\lambda }{6}}}{\lambda }} \right) = - 2cm\\ \to Ac{\rm{os}}\left( {\frac{{5\pi }}{6}} \right) = - 2 \to A = \frac{4}{{\sqrt 3 }}cm\end{array}$

Câu 10 :

A.

Đi qua vị trí cân bằng theo chiều dương
B.

Đi qua vị trí cân bằng theo chiều âm
C.

Ở vị trí biên dương
D.

Ở vị trí biên âm

Đáp án : B

Phương pháp giải :

+ Vận dụng biểu thức tính độ lệch pha: $\Delta \varphi = \frac{{2\pi x}}{\lambda }$

Lời giải chi tiết :

Từ phương trình sóng, ta có:

$\frac{{2\pi x}}{\lambda } = \pi x \to \lambda = 2m$

Độ lệch pha giữa 2 điểm M, N là:

$\Delta \varphi = \frac{{2\pi x}}{\lambda } = \frac{{2\pi .5}}{2} = 5\pi $

=> M và N dao động ngược pha nhau

=> Khi M đi qua vị trí cân bằng theo chiều dương thì N đi qua vị trí cân bằng theo chiều âm

Câu 11 :

Cho phương trình sóng: $u = a\sin \left( {0,4\pi x + 7\pi t + \dfrac{\pi }{3}} \right)\left( {m,s} \right)$. Phương trình này biểu diễn:

A.

Sóng chạy theo chiều âm của trục x với vận tốc $\dfrac{{10}}{7}$ (m/s)
B.

Sóng chạy theo chiều dương của trục x với vận tốc $\dfrac{{10}}{7}$ cm/s
C.

Sóng chạy theo chiều dương của trục x với vận tốc $17,5 (m/s)$
D.

Sóng chạy theo chiều âm của trục x với vận tốc $17,5 (m/s)$

Đáp án : D

Phương pháp giải :

+ Đọc các đại lượng trong phương trình dao động sóng

+ Áp dụng công thức: $\dfrac{{2\pi x}}{\lambda } = 0,4\pi x \to \lambda = \dfrac{2}{{0,4}} = 5m$

+ Áp dụng công thức tính vận tốc truyền sóng: $v = \lambda f$

Lời giải chi tiết :

Ta có:

$u = {\rm{a}}\sin \left( {7\pi t + 0,4\pi x + \dfrac{\pi }{3}} \right)(m,s)$

Ta thấy $"+0,4{\pi}x"$

=> Sóng chạy theo chiều âm của trục x

$\dfrac{{2\pi x}}{\lambda } = 0,4\pi x \to \lambda = \dfrac{2}{{0,4}} = 5m$

Vận tốc truyền sóng:

$v = \lambda f = \lambda \dfrac{\omega }{{2\pi }} = 5.\dfrac{{7\pi }}{{2\pi }} = 17,5m/s$

Câu 12 :

A.

2cm
B.

-2cm
C.

0cm
D.

-1,5cm

Đáp án : B

Phương pháp giải :

+ Áp dụng công thức tính tần số góc: $\omega = 2\pi f$

+ Vận dụng công thức tính góc quyét trong thời gian ∆t: $\Delta \varphi = \omega \Delta t$

+ Sử dụng vòng tròn lượng giác

Lời giải chi tiết :

Tần số góc:

$\omega = 2\pi f = 2\pi .50 = 100\pi \left( {ra{\rm{d}}/s} \right)$

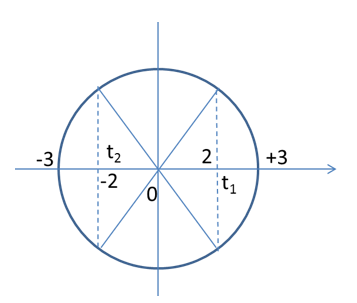
Góc quyét của M từ t₁ đến t₂ là:

$\Delta \varphi = \omega \Delta t = 100\pi .2,01 = 201\pi $

=> li độ của M tại t₁ và t₂ ngược pha nhau

=> tại t₂ M có li độ là -2cm

Câu 13 :

A.

10,3mm
B.

11,1mm
C.

5,15mm
D.

7,3mm

Đáp án : D

Phương pháp giải :

+ Sử dụng vòng tròn lượng giác

+ Sử dụng hệ thức ${\sin ^2}\alpha + c{\rm{o}}{{\rm{s}}^2}\alpha = 1$

Lời giải chi tiết :

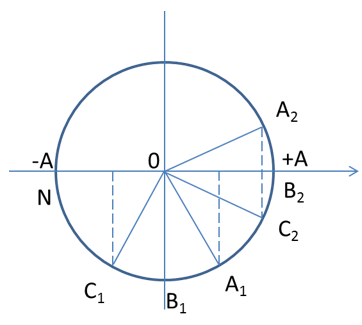
Xác định tọa độ các điểm tại các thời điểm t₁ và t₂

Từ vòng tròn lượng giác, ta có:

B quay góc 90⁰ => Tại t₂ li độ B chính bằng biên độ

A, C cũng tương tự

Ta có:

$\frac{{4,{8^2}}}{{{A^2}}} + \frac{{5,{5^2}}}{{{A^2}}} = 1 \to A = \sqrt {4,{8^2} + 5,{5^2}} = 7,3mm$

Câu 14 :

A.

${u_M} = 5\cos (4\pi t - 5\pi )(cm)$
B.

${u_M} = 5\cos (4\pi t - 2,5\pi )(cm)$
C.

${u_M} = 5\cos (4\pi t + \pi )(cm)$
D.

${u_M} = 5\cos (4\pi t - 25\pi )(cm)$

Đáp án : A

Phương pháp giải :

+ Áp dụng công thức tính bước sóng: $\lambda = vT$

+ Áp dụng công thức tính tần số góc: $\omega = \frac{{2\pi }}{T}$

+ Viết phương trình dao động của một điểm

Lời giải chi tiết :

Bước sóng:

$\lambda = vT = 40.0,5 = 20cm$

Tần số góc:

$\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,5}} = 4\pi ra{\rm{d}}/s$

PT sóng tại M:

${u_M} = 5c{\rm{os}}\left( {4\pi t - \frac{{2\pi d}}{\lambda }} \right) = 5c{\rm{os}}\left( {4\pi t - \frac{{2\pi .50}}{{20}}} \right) = 5c{\rm{os}}\left( {4\pi t - 5\pi } \right)$

Câu 15 :

A.

${u_M} = 5\cos (\omega t - \frac{{2\lambda }}{3})cm$
B.

${u_M} = 10\cos (\omega t - \frac{{\pi \lambda }}{3})cm$
C.

${u_M} = 10\cos (\omega t - \frac{{2\pi }}{3})cm$
D.

${u_M} = 5\cos (\omega t - \frac{\pi }{3})cm$

Đáp án : C

Lời giải chi tiết :

PT sóng tại O: $u = ac{\rm{os}}\omega {\rm{t}}\left( {cm} \right)$

PT sóng tại M:

${u_M} = ac{\rm{os}}\left( {\omega t \pm \frac{{2\pi d}}{\lambda }} \right) = ac{\rm{os}}\left( {\omega t \pm \frac{{2\pi \frac{\lambda }{3}}}{\lambda }} \right) = ac{\rm{os}}\left( {\omega t \pm \frac{{2\pi }}{3}} \right)$

Tại thời điểm t = 0,5T thì u = 5cm

$\begin{array}{l}{u_M} = ac{\rm{os}}\left( {\omega \frac{T}{2} \pm \frac{{2\pi }}{3}} \right) = ac{\rm{os}}\left( {\frac{{2\pi }}{T}.\frac{T}{2} \pm \frac{{2\pi }}{3}} \right)\\ = ac{\rm{os}}\left( {\frac{{2\pi }}{T}.\frac{T}{2} \pm \frac{{2\pi }}{3}} \right) = 5cm\\ \leftrightarrow ac{\rm{os}}\left( {\pi \pm \frac{{2\pi }}{3}} \right) = 5cm \to a = 10cm\end{array}$

=> Phương trình sóng tại M: ${u_M} = 10\cos (\omega t - \frac{{2\pi }}{3})cm$

Câu 16 :

A.

$u_M= 0,02cos2πt (m)$
B.

$u_M= 0,02cos(2πt + 3π/2) (m)$
C.

$u_M= 0,02cos(2πt - 3π/2) (m)$
D.

$u_M= 0,02cos(2πt - π) (m)$

Đáp án : C

Phương pháp giải :

+ Áp dụng biểu thức tính bước sóng: $\lambda = vT$

+ Viết phương trình dao động của một điểm

Lời giải chi tiết :

Bước sóng:

$\lambda = vT = v\dfrac{{2\pi }}{\omega } = 1,2\dfrac{{2\pi }}{{2\pi }} = 1,2m$

Sóng truyền từ N đến M, ta có phương trình sóng tại M là:

${u_M} = 0,02c{\rm{os}}\left( {2\pi t - \dfrac{{2\pi d}}{\lambda }} \right) = 0,02c{\rm{os}}\left( {2\pi t - \dfrac{{2\pi 0,9}}{{1,2}}} \right) = 0,02c{\rm{os}}\left( {2\pi t - \dfrac{{3\pi }}{2}} \right)m$

Câu 17 :

A.

${u_M} = 6\cos (5\pi t)cm$
B.

${u_M} = 6c{\rm{os}}\left( {5\pi t + \frac{\pi }{2}} \right)$ cm
C.

${u_M} = 6c{\rm{os}}\left( {5\pi t - \frac{\pi }{2}} \right)$ cm
D.

${u_M} = 6\cos (5\pi t + \pi )cm$

Đáp án : D

Phương pháp giải :

+ Áp dụng biểu thức tính bước sóng: $\lambda = vT$

+ Viết phương trình dao động của một điểm

Lời giải chi tiết :

Bước sóng:

$\lambda = vT = v\frac{{2\pi }}{\omega } = 5\frac{{2\pi }}{{5\pi }} = 2m$

Do M nằm trước O, ta có phương trình dao động của M là:

${u_M} = 6c{\rm{os}}\left( {5\pi t + \frac{\pi }{2} + \frac{{2\pi d}}{\lambda }} \right) = 6c{\rm{os}}\left( {5\pi t + \frac{\pi }{2} + \frac{{2\pi 0,5}}{2}} \right) = 6c{\rm{os}}\left( {5\pi t + \pi } \right)$

Câu 18 :

A.
${u_N} = 4cos\left( {\dfrac{{40\pi t}}{9} + \dfrac{{5\pi }}{9}} \right)cm.$
B.
${u_N} = 4cos\left( {\dfrac{{40\pi t}}{9} - \dfrac{{5\pi }}{9}} \right)cm.$
C.
${u_N} = 4cos\left( {\dfrac{{20\pi t}}{9} - \dfrac{{5\pi }}{9}} \right)cm$
D.
${u_N} = 4cos\left( {\dfrac{{20\pi t}}{9} + \dfrac{{5\pi }}{9}} \right)cm.$

Đáp án : C

Phương pháp giải :

+ Sử dụng biểu thức tính độ lệch pha: $\Delta \varphi = \dfrac{{2\pi d}}{\lambda }$

+ Sử dụng biểu thức: $\lambda = \dfrac{v}{f}$

Lời giải chi tiết :

+ Độ lệch pha giữa hai điểm gần nhau nhất cách nhau $6m$ trên phương truyền sóng dao động lệch pha nhau $\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi }}{3}$

$ \Rightarrow \lambda = \dfrac{{2\pi .6}}{{\dfrac{{2\pi }}{3}}} = 18m$

Lại có: $\lambda = \dfrac{v}{f} \Rightarrow f = \dfrac{v}{\lambda } = \dfrac{{20}}{{18}} = \dfrac{{10}}{9}Hz$

$ \Rightarrow \omega = 2\pi f = \dfrac{{20\pi }}{9}\left( {rad/s} \right)$

+ Phương trình sóng tại N: ${u_N} = 4cos\left( {\dfrac{{20\pi }}{9}t - \dfrac{\pi }{2} - \dfrac{{2\pi .ON}}{\lambda }} \right) = 4\cos \left( {\dfrac{{20\pi }}{9}t - \dfrac{{5\pi }}{9}} \right)cm$

Câu 19 :

A.
$2\sqrt 3 cm$.
B.
2cm.
C.
4cm.
D.
$\dfrac{{4\sqrt 3 }}{3}cm$

Đáp án : C

Phương pháp giải :

Phương trình sóng tại nguồn: ${u_O} = A.\cos \left( {\dfrac{{2\pi t}}{T}} \right)cm$

Phương trình sóng tại M cách O một khoảng x: ${u_M} = A.\cos \left( {\dfrac{{2\pi t}}{T} - \dfrac{{2\pi .x}}{\lambda }} \right)cm$

Thay $t = \dfrac{T}{2}$ vào phương trình của u_M suy ra được A

Lời giải chi tiết :

Phương trình sóng tại M cách O một khoảng $\dfrac{1}{3}$ bước sóng là:

${u_M} = A.\cos \left( {\dfrac{{2\pi t}}{T} - \dfrac{{2\pi .\dfrac{\lambda }{3}}}{\lambda }} \right) = A.\cos \left( {\dfrac{{2\pi t}}{T} - \dfrac{{2\pi }}{3}} \right)cm$

Tại $t = \dfrac{T}{2}$ li độ u_M = 2cm. Ta có:

${u_M} = 2 \Leftrightarrow A.\cos \left( {\dfrac{{2\pi .\dfrac{T}{2}}}{T} - \dfrac{{2\pi }}{3}} \right) = 2cm \Rightarrow A = \dfrac{2}{{\cos \dfrac{\pi }{3}}} = 4cm$

Trắc nghiệm Bài 7. Đồ thị sóng cơ học - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 7. Đồ thị sóng cơ học Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 8. Giao thoa sóng - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 8. Giao thoa sóng Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 8. Xác định cực đại - cực tiểu giao thoa sóng - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 8. Xác định cực đại - cực tiểu giao thoa sóng Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 8. Phương trình sóng cơ tại một điểm trong trường giao thoa - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 8. Phương trình sóng cơ tại một điểm trong trường giao thoa Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 8. Pha dao động tại một điểm trong trường giao thoa - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 8. Pha dao động tại một điểm trong trường giao thoa Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 9. Sóng dừng - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 9. Sóng dừng Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 10. Sóng âm - Các đặc trưng vật lí và sinh lí của âm - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 10. Sóng âm - Các đặc trưng vật lí và sinh lí của âm Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Tổng hợp bài tập sóng cơ - sóng âm (phần 1) - Vật Lí 12

Luyện tập và củng cố kiến thức Tổng hợp bài tập sóng cơ - sóng âm (phần 1) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Tổng hợp bài tập sóng cơ - sóng âm (phần 2) - Vật Lí 12

Luyện tập và củng cố kiến thức Tổng hợp bài tập sóng cơ - sóng âm (phần 2) Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Ôn tập chương 2 - Vật Lí 12

Luyện tập và củng cố kiến thức Ôn tập chương 2 Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 7. Các đại lượng đặc trưng cơ bản của sóng cơ - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 7. Các đại lượng đặc trưng cơ bản của sóng cơ Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 7. Sóng cơ và sự truyền sóng cơ - Vật Lí 12

Luyện tập và củng cố kiến thức Bài 7. Sóng cơ và sự truyền sóng cơ Vật lí 12 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Bài giải mới nhất

Trắc nghiệm Bài 7. Phương trình sóng cơ học - Vật Lí 12

Báo lỗi góp ý