 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 Bài 2. Tổng của hai vectơ
Bài 2. Tổng của hai vectơ
Bài 9 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Các hệ thức sau đây đúng hay sai
Các hệ thức sau đây đúng hay sai (với mọi \(\overrightarrow a \) và \(\overrightarrow b \) )?
LG a
\(\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)
Phương pháp giải:
Chứng minh \(\left| {\overrightarrow a + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\) bằng cách dựng hình và sử dụng bất đẳng thức tam giác.
Từ đó suy ra tính đúng sai của mỗi câu.
Lời giải chi tiết:
Ta sẽ chứng minh \(\left| {\overrightarrow a + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)
Chứng minh:
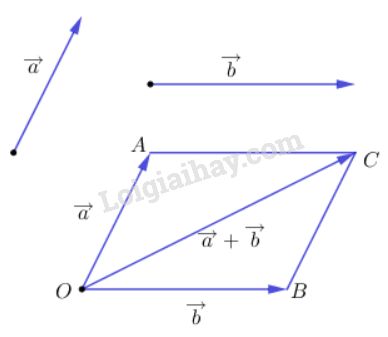
Từ một điểm \(O\) trong mặt phẳng ta dựng vectơ:
\(\eqalign{
& \overrightarrow {OA} = \overrightarrow a \cr
& \overrightarrow {OB} = \overrightarrow b \cr} \)
Và dựng hình bình hành \(OACB\) \( \Rightarrow \overrightarrow {AC} = \overrightarrow {OB} \)
Như vậy:
\(\eqalign{
& OA = |\overrightarrow {OA} | = |\overrightarrow a | \cr
& OB = |\overrightarrow {OB} | = |\overrightarrow b | \cr&\Rightarrow AC = |\overrightarrow {AC} |=|\overrightarrow {OB} | = |\overrightarrow b | \cr
& \overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \Rightarrow \overrightarrow {OC} = \overrightarrow a + \overrightarrow b \cr
& OC = |\overrightarrow {OC} | = |\overrightarrow a + \overrightarrow b | \cr} \)
Áp dụng bất đẳng thức tam giác vào tam giác \(OAC\), ta có:
\(OA + AC ≥ OC \) \(\Rightarrow \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \ge \left| {\overrightarrow a + \overrightarrow b } \right|\)
\( ⇒ |\overrightarrow a + \overrightarrow b | \le |\overrightarrow a | + |\overrightarrow {b|} \).
Dấu "=" xảy ra khi OA+AC=OC hay A nằm giữa O và C.
Khi đó \(\overrightarrow {OA} ,\overrightarrow {AC} \) cùng hướng hay \(\overrightarrow a ,\overrightarrow b \) cùng hướng. (Do \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {AC} = \overrightarrow b \))
Chú ý:
Các em cũng không nhất thiết phải dựng hình bình hành. Có thể dựng hình cách khác như sau:
Từ điểm O dựng điểm A sao cho \(\overrightarrow {OA} = \overrightarrow a \).
Từ điểm A dựng điểm C sao cho \(\overrightarrow {AC} = \overrightarrow b \).
Rồi sử dụng bất đẳng thức tam giác cũng ra được đpcm.
Do đó a sai.
LG b
\(\left| {\overrightarrow a + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)
Lời giải chi tiết:
Đúng.
Loigiaihay.com
- Bài 10 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao
- Bài 11 trang 14 sách giáo khoa (SGK) Hình học 10 Nâng cao
- Bài 12 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao
- Bài 13 trang 15 Sách giáo khoa (SGK) Hình học 10 Nâng cao
- Bài 8 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao
>> Xem thêm












Danh sách bình luận