Bài 12 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao

LG a

Hãy xác định các điểm \(M, N, P\) sao cho

\(\overrightarrow {OM}  = \overrightarrow {OA}  + \overrightarrow {OB} \,;\)

\(\overrightarrow {ON}  = \overrightarrow {OB}  + \overrightarrow {OC} \,;\)

\(\overrightarrow {OP}  = \overrightarrow {OC}  + \overrightarrow {OA} \)

Lời giải chi tiết:

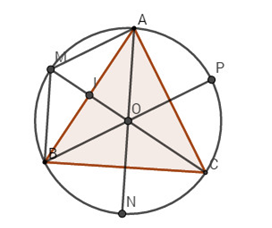
\(\overrightarrow {OM}  = \overrightarrow {OA}  + \overrightarrow {OB} \) \( \Leftrightarrow \) M là đỉnh còn lại của hình bình hành AOBM.

AOBM là hình bình hành ⇒ AM//BO

\(\begin{array}{l} \Rightarrow \widehat {MAO} + \widehat {AOB} = {180^0}\\ \Leftrightarrow \widehat {MAO} + {120^0} = {180^0}\\ \Rightarrow \widehat {MAO} = {60^0}\end{array}\)

Ta có: \(\widehat {MAO} = {60^0},\widehat {OAC} = {30^0}\) \( \Rightarrow \widehat {MAC} = \widehat {MAO} + \widehat {OAC}\) \( = {60^0} + {30^0} = {90^0}\)

\( \Rightarrow MA \bot AC\)\( \Rightarrow CM\)  là đường kính của đường tròn tâm O.

Vậy điểm \(M\) là điểm sao cho \(CM\) là đường kính của đường tròn tâm \(O\).

Tương tự, ta cũng có \(N, P\) thuộc đường tròn \((O)\) sao cho \(AN, BP\) là đường kính của đường tròn \((O)\).

Cách khác:

Kéo dài \(OC\) cắt đường tròn tại điểm \(M\).

MC là đường kính nên \(\widehat {MBC} = {90^0} \Rightarrow MB \bot BC\).

Mà tam giác ABC đều nên \(AO\bot BC\).

Do đó MB//OA (1)

Lại có \(\widehat {MAC} = {90^0} \Rightarrow MA \bot AC\).

Mà tam giác ABC đều nên \(BO\bot AC\).

Do đó MA//BO (2)

Từ (1) và (2) suy ra \(OAMB\) là hình bình hành, suy ra:

\(\overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OM} \).

Vậy M là điểm cần tìm.

LG b

Chứng minh rằng \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow 0 \).

Lời giải chi tiết:

\(O\) là trung điểm của \(MC\) nên \(\overrightarrow {OM}  + \overrightarrow {OC}  = \overrightarrow 0 \), mà \(\overrightarrow {OM}  = \overrightarrow {OA}  + \overrightarrow {OB} \) suy ra \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow 0 \)

Loigiaihay.com