Giải SBT toán hình học và đại số 10 nâng cao BÀI TẬP ÔN TẬP CUỐI NĂM - HÌNH HỌC 10 NÂNG CAO

Bài 6 trang 189 SBT Hình học 10 Nâng cao


Cho đường tròn (O ; R) và một đường thẳng d

Đề bài

Cho đường tròn (O ; R) và một đường thẳng d không cắt đường thẳng đó. Một điểm I thay đổi trên d. Kẻ tiếp tuyến IT tới đường tròn với T là tiếp điểm. Gọi (I) là đường tròn tâm I bán kính r=IT. Chứng minh rằng các đường tròn (I) luôn đi qua hai điểm cố định khi I thay đổi.

Lời giải chi tiết

(h.139).

 

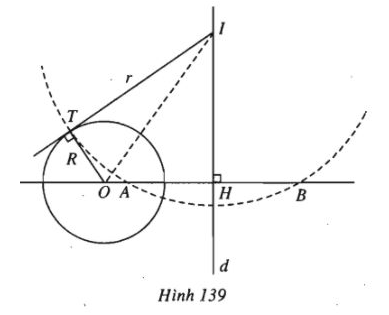
Từ O kẻ đường  thẳng vuông góc với d tại H. Hai tam giác vuông OHI và OTI có chung cạnh huyền OI, còn OH > OT=R ( vì d không cắt (O)). Suy ra IH < IT.

Vậy đường thẳng OH cắt đường tròn (I) tại hai điểm A và B nào đó đối xứng với nhau qua d.

Ta có

Bởi vậy, nếu đặt OH=h thì \(HA = HB = \sqrt {{h^2} - {R^2}} \). Suy ra (I) đi qua hai điểm A,B cố định.

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store