Giải SBT toán hình học và đại số 10 nâng cao BÀI TẬP ÔN TẬP CUỐI NĂM - HÌNH HỌC 10 NÂNG CAO

Bài 4 trang 188 SBT Hình học 10 Nâng cao


Giải bài tập Bài 4 trang 188 SBT Hình học 10 Nâng cao

Đề bài

Trên các cạnh \(AC\) và \(BC\) của tam giác \(ABC\) lần lượt lấy các điểm \(M\) và \(N\) sao cho \( \dfrac{{AM}}{{MC}} =  \dfrac{{NC}}{{NB}} = k\), trên \(MN\) lấy điểm \(P\) sao cho \( \dfrac{{PM}}{{PN}} = k\). Gọi \(S, S_1\) và \(S_2\) lần lượt là diện tích các tam giác \(ABC, APM\) và \(BPN\). Chứng minh \(\sqrt[3]{S} = \sqrt[3]{{{S_1}}} + \sqrt[3]{{{S_2}}}\).

 

Lời giải chi tiết

(h.137).

 

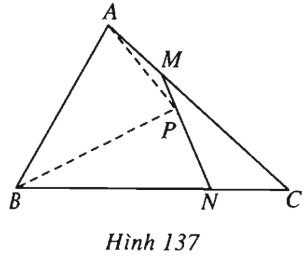
Từ giả thiết\( \dfrac{{AM}}{{MC}} = k\), ta suy ra: \( \dfrac{{AM}}{{AC}} =  \dfrac{k}{{k + 1}}\) và \( \dfrac{{MC}}{{AC}} =  \dfrac{1}{{k + 1}}\).

Tương tự như thế:

\( \dfrac{{NC}}{{BC}} =  \dfrac{k}{{k + 1}}  ,\) \(   \dfrac{{NB}}{{BC}} =  \dfrac{1}{{k + 1}}  , \) \(  \dfrac{{PM}}{{MN}} =  \dfrac{k}{{k + 1}}  , \) \(  \dfrac{{PN}}{{MN}} =  \dfrac{1}{{k + 1}}\).

Từ đó suy ra :

\(\begin{array}{l}{S_1} = {S_{APM}} =  \dfrac{k}{{k + 1}}{S_{AMN}} \\=  \dfrac{k}{{k + 1}}. \dfrac{k}{{k + 1}}{S_{ACN}}\\       =  \dfrac{k}{{k + 1}}. \dfrac{k}{{k + 1}}. \dfrac{k}{{k + 1}}{S_{ABC}}\\ = {\left( { \dfrac{k}{{k + 1}}} \right)^3}S.\end{array}\)

Tính toán tương tự, ta có \({S_2} = {\left( { \dfrac{1}{{k + 1}}} \right)^3}S\).

Vậy \(\sqrt[3]{{{S_1}}} + \sqrt[3]{{{S_2}}} =  \dfrac{k}{{k + 1}}\sqrt[3]{S} +  \dfrac{1}{{k + 1}}\sqrt[3]{S}\)

\(= \sqrt[3]{S}\).

Loigiaihay.com

 

Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

2k8 Tham gia ngay group chia sẻ, trao đổi tài liệu học tập miễn phí

>> Học trực tuyến Lớp 10 tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua