Bài 55 trang 14 SBT Hình học 10 Nâng cao

Giải bài 55 trang 14 sách bài tập Hình học 10 Nâng cao. Cho G là trọng tâm tam giác ABC. Trên cạnh AB lấy hai điểm M và N sao cho AM=MN=NB...

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

Cho \(G\) là trọng tâm tam giác \(ABC\). Trên cạnh \(AB\) lấy hai điểm \(M\) và \(N\) sao cho \(AM=MN=NB\).

LG a

Chứng tỏ rằng \(G\) cũng là trọng tâm tam giác \(MNC\).

Lời giải chi tiết:

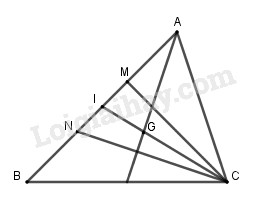
Gọi \(I\) là trung điểm \(MN\) thì \(I\) cũng là trung điểm \(AB\), do đó

\(\overrightarrow {GM} + \overrightarrow {GN} = 2\overrightarrow {GI} = \overrightarrow {GA} + \overrightarrow {GB} \)

Suy ra

\(\overrightarrow {GM} + \overrightarrow {GN} + \overrightarrow {GC} \)

\(= \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).

Vậy \(G\) cũng là trọng tâm của tam giác \(MNC.\)

LG b

Đặt \(\overrightarrow {GA} = \overrightarrow a ,\,\,\overrightarrow {GB} = \overrightarrow b \). Hãy biểu thị các vec tơ sau đây qua \(\overrightarrow a \) và \(\overrightarrow b \): \(\overrightarrow {GC} ,\,\overrightarrow {AC} ,\,\overrightarrow {GM} ,\,\overrightarrow {CN} \).

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}
\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \\
\Rightarrow \overrightarrow {GC} = - \overrightarrow {GA} - \overrightarrow {GB} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \overrightarrow a - \overrightarrow b \\
\overrightarrow {AC} = \overrightarrow {GC} - \overrightarrow {GA} \\
\,\,\,\,\,\,\,\,\, = - \overrightarrow a - \overrightarrow b - \overrightarrow a \\
\,\,\,\,\,\,\,\,\, = - 2\overrightarrow a - \overrightarrow b
\end{array}\)

\(\begin{array}{l}\overrightarrow {GM} = \overrightarrow {GA} + \overrightarrow {AM} \\ = \overrightarrow {GA} + \frac{1}{3}\overrightarrow {AB} \\ = \overrightarrow {GA} + \frac{1}{3}\left( {\overrightarrow {GB} - \overrightarrow {GA} } \right)\\= \overrightarrow a + \dfrac{1}{3}(\overrightarrow b - \overrightarrow a ) \\= \dfrac{{2\overrightarrow a + \overrightarrow b }}{3}.\\\overrightarrow {CN} = \overrightarrow {CA} + \overrightarrow {AN} \\ = - \overrightarrow {AC} + \frac{2}{3}\overrightarrow {AB} \\= - \overrightarrow {AC} + \frac{2}{3}\left( {\overrightarrow {GB} - \overrightarrow {GA} } \right)\\ = 2\overrightarrow a + \overrightarrow b + \dfrac{2}{3}(\overrightarrow b - \overrightarrow a )\\ = \dfrac{{4\overrightarrow a + 5\overrightarrow b }}{3}.\end{array}\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 56 trang 14 SBT Hình học 10 Nâng cao
Giải bài 56 trang 14 sách bài tập Hình học 10 Nâng cao. Cho tam giác ABC. Hãy xác định các điểm M, N, P sao cho:...
Bài 57 trang 14 SBT Hình học 10 Nâng cao
Giải bài 57 trang 14 sách bài tập Hình học 10 Nâng cao. Cho tam giác ABC, với mỗi số k ta xác định các điểm A’, B’, sao cho ...
Bài 58 trang 15 SBT Hình học 10 Nâng cao
Giải bài 58 trang 15 sách bài tập Hình học 10 Nâng cao. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(4;0), B(2;-2). Đường thẳng AB cắt trục Oy tại điểm M. Trong ba điểm A, B, M điểm nào nằm giữa hai điểm còn lại.
Bài tập trắc nghiệm trang 15, 16, 17 SBT Hình học 10 Nâng cao
Giải bài tập trắc nghiệm trang 15, 16, 17 sách bài tập Hình học 10 Nâng cao. Chọn đáp án đúng:...
Bài 54 trang 14 SBT Hình học 10 Nâng cao
Giải bài 54 trang 14 sách bài tập Hình học 10 Nâng cao. Tứ giác ABCD là hình gì nếu thỏa mãn một trong các điều kiện sau đây?...
Bài 53 trang 14 SBT Hình học 10 Nâng cao
Giải bài 53 trang 14 sách bài tập Hình học 10 Nâng cao. Tam giác ABC là tam giác gì nếu nó thỏa mãn một trong các điều kiện sau đây?