Bài tập trắc nghiệm trang 15, 16, 17 SBT Hình học 10 Nâng cao
Giải bài tập trắc nghiệm trang 15, 16, 17 sách bài tập Hình học 10 Nâng cao. Chọn đáp án đúng:...
Chọn đáp án đúng:
Bài 1
Cho tam giác đều \(ABC\) có cạnh \(a\). Độ dài của tổng hai vec tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) bằng bao nhiêu?
A. \(2a;\) B. \(a;\)
C. \(a\sqrt 3;\) D. \(\dfrac{{a\sqrt 3 }}{2}.\)
Lời giải chi tiết:
Chọn (C).
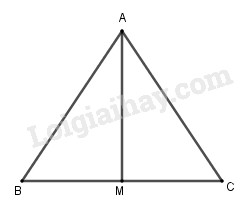
Gọi M là trung điểm của BC thì
\(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right|\)\( = 2\left| {\overrightarrow {AM} } \right| = 2AM\)
Tam giác ABM vuông tại M nên theo định lý Pitago ta có:
\(AM = \sqrt {A{B^2} - B{M^2}} \) \( = \sqrt {{a^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 3 }}{2}\)
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2AM\) \( = 2.\dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \)
Bài 2
Cho tam giác vuông cân \(ABC\) có \(AB=AC=a\). Độ dài của tổng hai vec tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) bằng bao nhiêu?
A. \(a\sqrt 2;\) B. \(\dfrac{{a\sqrt 2 }}{2};\)
C. \(2a;\) D. \(a.\)
Lời giải chi tiết:
Chọn (A).
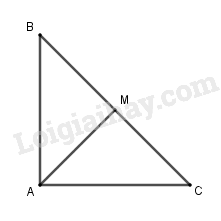
Tam giác ABC vuông nên \(BC = \sqrt {A{B^2} + A{C^2}} \) \( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow AM = \dfrac{1}{2}BC = \dfrac{{a\sqrt 2 }}{2}\)
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right|\) \( = 2\left| {\overrightarrow {AM} } \right| = 2AM\) \( = 2.\dfrac{{a\sqrt 2 }}{2} = a\sqrt 2 \)
Bài 3
Cho tam giác \(ABC\) vuông tại \(A\) và \(AB=3, AC=4\). Vec tơ \(\overrightarrow {CB} + \overrightarrow {AB} \) có độ dài bằng bao nhiêu?
A. \(2;\) B. \(2\sqrt {13};\)
C. \(4;\) D. \(\sqrt {13}.\)
Lời giải chi tiết:
Chọn (B).
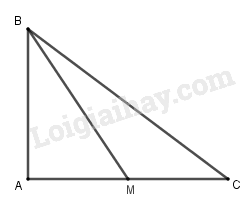
Gọi M là trung điểm của AC thì:
\(\begin{array}{l}\left| {\overrightarrow {CB} + \overrightarrow {AB} } \right| = \left| { - \overrightarrow {BC} - \overrightarrow {BA} } \right|\\ = \left| {\overrightarrow {BC} + \overrightarrow {BA} } \right| = \left| {2\overrightarrow {BM} } \right|\\ = 2BM = 2\sqrt {A{B^2} + A{M^2}} \\ = 2\sqrt {{3^2} + {2^2}} = 2\sqrt {13} \\ \Rightarrow \left| {\overrightarrow {CB} + \overrightarrow {AB} } \right| = 2\sqrt {13} \end{array}\)
Bài 4
Cho tam giác đều \(ABC\) có cạnh bằng \(a, \) \(H\) là trung điểm của cạnh \(BC\). Vec tơ \(\overrightarrow {CA} - \overrightarrow {HC} \) có độ dài bằng bao nhiêu?
A. \(\dfrac{a}{2};\) B. \(\dfrac{{3a\,}}{2};\)
C. \(\dfrac{{2a\sqrt 3 }}{3};\) D. \(\dfrac{{a\sqrt 7 }}{2}.\)
Lời giải chi tiết:
Chọn (D).
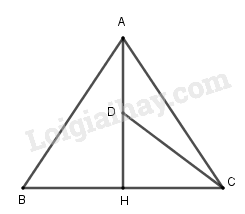
Gọi D là trung điểm của AH ta có:
\(\left| {\overrightarrow {CA} - \overrightarrow {HC} } \right| = \left| {\overrightarrow {CA} + \overrightarrow {CH} } \right|\) \( = \left| {2\overrightarrow {CD} } \right| = 2CD\)
Ta có:
\(AH = \sqrt {A{C^2} - C{H^2}} \) \( = \sqrt {{a^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 3 }}{2}\)
\( \Rightarrow DH = \dfrac{1}{2}AH\) \( = \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{4}\)
\( \Rightarrow CD = \sqrt {C{H^2} + D{H^2}} \) \( = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{4}} \right)}^2}} = \dfrac{{a\sqrt 7 }}{4}\)
\( \Rightarrow \left| {\overrightarrow {CA} - \overrightarrow {HC} } \right| = 2CD\)\( = 2.\dfrac{{a\sqrt 7 }}{4} = \dfrac{{a\sqrt 7 }}{2}\)
Bài 5
Gọi \(G\) là trọng tâm tam giác vuông \(ABC\) với cạnh huyền \(BC=12\). Tổng hai vec tơ \(\overrightarrow {GB} + \overrightarrow {GC} \) có độ dài bằng bao nhiêu?
A. \(2;\) B. \(2\sqrt 3\)
C. \(8\) D. \(4.\)
Lời giải chi tiết:
Chọn (D).
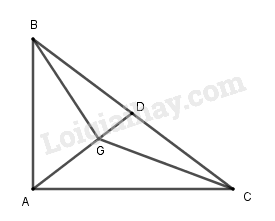
Gọi D là trung điểm của BC ta có:
\(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right| = \left| {2\overrightarrow {GD} } \right| = 2GD\) \( = 2.\dfrac{1}{3}AD = \dfrac{2}{3}AD\) \( = \dfrac{2}{3}.\dfrac{1}{2}BC = \dfrac{1}{3}.12 = 4\)
Bài 6
Cho bốn điểm \(A, B, C, D\). Gọi \(I\) và \(J\) lần lượt là trung điểm của các đoạn thẳng \(AB\) và \(CD\). Trong các đẳng thức dưới đây, đẳng thức nào sai?
A. \(2\overrightarrow {IJ} = \overrightarrow {AB} + \overrightarrow {CD} ;\)
B. \(2\overrightarrow {IJ} = \overrightarrow {AC} + \overrightarrow {BD} ;\)
C. \(2\overrightarrow {IJ} = \overrightarrow {AD} + \overrightarrow {BC} ;\)
D. \(2\overrightarrow {IJ} + \overrightarrow {CA} + \overrightarrow {DB} = \overrightarrow 0 .\)
Lời giải chi tiết:
Chọn (A).
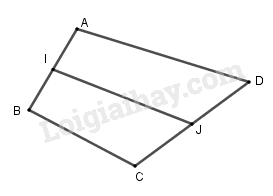
Ta có:
\(\begin{array}{l}\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AD} + \overrightarrow {DJ} \\\overrightarrow {IJ} = \overrightarrow {IB} + \overrightarrow {BC} + \overrightarrow {CJ} \\ \Rightarrow 2\overrightarrow {IJ} = \overrightarrow {IJ} + \overrightarrow {IJ} \\ = \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {DJ} + \overrightarrow {CJ} } \right)\\ = \overrightarrow 0 + \left( {\overrightarrow {AD} + \overrightarrow {BC} } \right) + \overrightarrow 0 \\ = \overrightarrow {AD} + \overrightarrow {BC} \,\,\,\,\,\left( {C\,\text{đúng}} \right)\\ = \overrightarrow {AC} + \overrightarrow {CD} + \overrightarrow {BD} + \overrightarrow {DC} \\ = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DC} } \right)\\ = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow 0 \\ = \overrightarrow {AC} + \overrightarrow {BD} \,\,\,\,\,\left( {B\,\text{đúng}} \right)\\ = - \overrightarrow {CA} - \overrightarrow {DB} \\ \Rightarrow 2\overrightarrow {IJ} + \overrightarrow {CA} + \overrightarrow {DB} = \overrightarrow 0 \,\,\left( {D\,\text{đúng}} \right)\\ \Rightarrow A\,sai.\end{array}\)
Bài 7
Cho sáu điểm \(A, B, C, D, E, F.\) Trong các đẳng thức dưới đây, đẳng thức nào sai?
A. \(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AE} + \overrightarrow {BD} + \overrightarrow {CF} ;\)
B. \(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CE} ;\)
C. \(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} ;\)
D. \(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AF} + \overrightarrow {BE} + \overrightarrow {CD} .\)
Lời giải chi tiết:
Chọn (B).
Ta có:
\(\begin{array}{l}\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} \\ = \overrightarrow {AE} + \overrightarrow {ED} + \overrightarrow {BD} + \overrightarrow {DE} + \overrightarrow {CF} \\ = \left( {\overrightarrow {AE} + \overrightarrow {BD} } \right) + \left( {\overrightarrow {ED} + \overrightarrow {DE} } \right) + \overrightarrow {CF} \\ = \overrightarrow {AE} + \overrightarrow {BD} + \overrightarrow {CF} \end{array}\)
Nên A đúng.
\(\begin{array}{l}\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} \\ = \overrightarrow {AE} + \overrightarrow {ED} + \overrightarrow {BF} + \overrightarrow {FE} + \overrightarrow {CE} + \overrightarrow {EF} \\ = \left( {\overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CE} } \right) + \left( {\overrightarrow {ED} + \overrightarrow {FE} + \overrightarrow {EF} } \right)\\ = \left( {\overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CE} } \right) + \overrightarrow {ED} \\ \ne \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CE} \end{array}\)
Nên B sai.
Bài 8
Cho tam giác \(ABC\) và điểm \(I\) sao cho \(\overrightarrow {IA} = 2\overrightarrow {IB} \). Biểu thị vec tơ \(\overrightarrow {CI} \) theo hai vec tơ \(\overrightarrow {CA} \) và \(\overrightarrow {CB} \) như sau:
A. \(\overrightarrow {CI} = \dfrac{{\overrightarrow {CA} - 2\overrightarrow {CB} }}{3};\)
B. \(\overrightarrow {CI} = - \overrightarrow {CA} + 2\overrightarrow {CB} ;\)
C. \(\overrightarrow {CI} = \dfrac{{\overrightarrow {CA} + 2\overrightarrow {CB} }}{3};\)
D. \(\overrightarrow {CI} = \dfrac{{\overrightarrow {CA} + 2\overrightarrow {CB} }}{{ - 3}}.\)
Lời giải chi tiết:
Chọn (B).
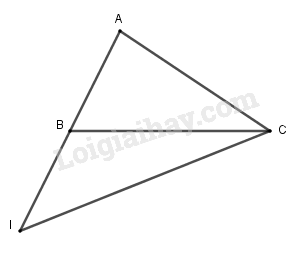
\(\begin{array}{l}\overrightarrow {IA} = 2\overrightarrow {IB} \\ \Rightarrow \overrightarrow {CA} - \overrightarrow {CI} = 2\left( {\overrightarrow {CB} - \overrightarrow {CI} } \right)\\ \Leftrightarrow \overrightarrow {CA} - \overrightarrow {CI} = 2\overrightarrow {CB} - 2\overrightarrow {CI} \\ \Leftrightarrow \overrightarrow {CA} - 2\overrightarrow {CB} = - \overrightarrow {CI} \\ \Leftrightarrow \overrightarrow {CI} = - \overrightarrow {CA} + 2\overrightarrow {CB} \end{array}\)
Bài 9
Cho tam giác \(ABC\) và \(I\) là điểm sao cho \(\overrightarrow {IA} + 2\overrightarrow {IB} = \overrightarrow 0 \). Biểu thị vec tơ \(\overrightarrow {CI} \) theo hai vec tơ \(\overrightarrow {CA} \) và \(\overrightarrow {CB} \) như sau:
A. \(\overrightarrow {CI} = \dfrac{{\overrightarrow {CA} - 2\overrightarrow {CB} }}{3};\)
B. \(\overrightarrow {CI} = - \overrightarrow {CA} + 2\overrightarrow {CB} ;\)
C. \(\overrightarrow {CI} = \dfrac{{\overrightarrow {CA} + 2\overrightarrow {CB} }}{3};\)
D. \(\overrightarrow {CI} = \dfrac{{\overrightarrow {CA} + 2\overrightarrow {CB} }}{{ - 3}}.\)
Lời giải chi tiết:
Chọn (C).
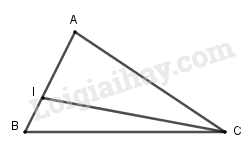
\(\begin{array}{l}\overrightarrow {IA} + 2\overrightarrow {IB} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {CA} - \overrightarrow {CI} + 2\left( {\overrightarrow {CB} - \overrightarrow {CI} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {CA} + 2\overrightarrow {CB} - 3\overrightarrow {CI} = \overrightarrow 0 \\ \Leftrightarrow 3\overrightarrow {CI} = \overrightarrow {CA} + 2\overrightarrow {CB} \\ \Leftrightarrow \overrightarrow {CI} = \dfrac{{\overrightarrow {CA} + 2\overrightarrow {CB} }}{3}\end{array}\)
Bài 10
Cho tam giác \(ABC\) với trọng tâm \(G\). Đặt \(\overrightarrow {CA} = \overrightarrow a ,\,\,\overrightarrow {CB} = \overrightarrow b \). Biểu thị vec tơ \(\overrightarrow {AG} \) theo hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) như sau:
A. \(\overrightarrow {AG} = \dfrac{{2\overrightarrow a - \overrightarrow b }}{3};\)
B. \(\overrightarrow {AG} = \dfrac{{2\overrightarrow a + \overrightarrow b }}{3};\)
C. \(\overrightarrow {AG} = \dfrac{{\overrightarrow a - 2\overrightarrow b }}{3};\)
D. \(\overrightarrow {AG} = \dfrac{{ - 2\overrightarrow a + \overrightarrow b }}{3}.\)
Lời giải chi tiết:
Chọn (D).
G là trọng tâm tam giác ABC thì với điểm M bất kì ta có:
\(\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \\ \Leftrightarrow \overrightarrow {MG} = \dfrac{1}{3}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\end{array}\)
Lấy \(M \equiv A\) ta có:
\(\begin{array}{l}\overrightarrow {AG} = \dfrac{1}{3}\left( {\overrightarrow {AA} + \overrightarrow {AB} + \overrightarrow {AC} } \right)\\ \Leftrightarrow \overrightarrow {AG} = \dfrac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\\ \Leftrightarrow \overrightarrow {AG} = \dfrac{1}{3}\left( {\overrightarrow {CB} - \overrightarrow {CA} - \overrightarrow {CA} } \right)\\ \Leftrightarrow \overrightarrow {AG} = \dfrac{1}{3}\left( { - 2\overrightarrow {CA} + \overrightarrow {CB} } \right)\\ \Leftrightarrow \overrightarrow {AG} = \dfrac{{ - 2\overrightarrow a + \overrightarrow b }}{3}\end{array}\)
Bài 11
Cho \(G\) là trọng tâm tam giác \(ABC\). Đặt \(\overrightarrow {CA} = \overrightarrow a ,\,\,\overrightarrow {CB} = \overrightarrow b \). Biểu thị vec tơ \(\overrightarrow {CG} \) theo hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) như sau:
A. \(\overrightarrow {CG} = \dfrac{{\overrightarrow a + \overrightarrow b }}{3};\)
B. \(\overrightarrow {CG} = \dfrac{{2(\overrightarrow a + \overrightarrow b) }}{3};\)
C. \(\overrightarrow {CG} = \dfrac{{\overrightarrow a - \overrightarrow b }}{3};\)
D. \(\overrightarrow {CG} = \dfrac{{ 2(\overrightarrow a - \overrightarrow b) }}{3}.\)
Lời giải chi tiết:
Chọn (A).
G là trọng tâm tam giác ABC thì với điểm M bất kì ta có:
\(\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \\ \Leftrightarrow \overrightarrow {MG} = \dfrac{1}{3}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\end{array}\)
Lấy \(M \equiv C\) ta có:
\(\begin{array}{l}\overrightarrow {CG} = \dfrac{1}{3}\left( {\overrightarrow {CA} + \overrightarrow {CB} + \overrightarrow {CC} } \right)\\ \Leftrightarrow \overrightarrow {CG} = \dfrac{1}{3}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)\\ \Leftrightarrow \overrightarrow {CG} = \dfrac{1}{3}\left( {\overrightarrow a + \overrightarrow b } \right)\\ \Leftrightarrow \overrightarrow {CG} = \dfrac{{\overrightarrow a + \overrightarrow b }}{3}\end{array}\)
Bài 12
Trong hệ tọa độ \(Oxy\) cho các điểm \(A(1;-2), B(0;3), C(-3;4), D(-1;8)\). Ba điểm nào trong bốn điểm là ba điểm thẳng hàng?
A. \(A, B, C;\) B. \(B, C, D;\)
C. \(A, B, D;\) D. \( A, C, D.\)
Lời giải chi tiết:
Chọn (C).
Ta có:
\(\begin{array}{l}\overrightarrow {AB} = \left( { - 1;5} \right),\overrightarrow {AD} = \left( { - 2;10} \right)\\ \Rightarrow \overrightarrow {AD} = 2\overrightarrow {AB} \end{array}\)
\( \Rightarrow A,B,D\) thẳng hàng.
Bài 13
Trong hệ tọa độ \(Oxy\) cho ba điểm \(A(1;3), B(-3;4)\) và \(G(0;3)\). Tìm tọa độ điểm \(C\) sao cho \(G\) là trọng tâm tam giác \(ABC.\)
A. \((2;2);\) B. \((-2;2);\)
C. \((2;0);\) D. \((0;2).\)
Lời giải chi tiết:
Chọn (A).
G là trọng tâm \(\Delta ABC\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0 = \dfrac{{1 + \left( { - 3} \right) + {x_C}}}{3}\\3 = \dfrac{{3 + 4 + {y_C}}}{3}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 2 + {x_C} = 0\\7 + {y_C} = 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 2\\{y_C} = 2\end{array} \right.\\ \Rightarrow C\left( {2;2} \right)\end{array}\)
Bài 14
Trong hệ tọa độ \(Oxy\) cho hình bình hành \(ABCD\), biết \(A(1;3), B(-2;0), C(2;-1)\). Hãy tìm tọa độ điểm \(D\).
A. \((2;2);\) B. \((5;2);\)
C. \((4;-1);\) D. \((2;5).\)
Lời giải chi tiết:
Chọn (B).
ABCD là hình bình hành
\(\begin{array}{l} \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \\ \Leftrightarrow \left\{ \begin{array}{l} - 2 - 1 = 2 - {x_D}\\0 - 3 = - 1 - {y_D}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 3 = 2 - {x_D}\\ - 3 = - 1 - {y_D}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 5\\{y_D} = 2\end{array} \right.\\ \Rightarrow D\left( {5;2} \right)\end{array}\)
Loigiaihay.com












Danh sách bình luận