Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học

Ôn tập chương 2

Bài 44 trang 64 SGK Đại số 10 nâng cao

Vẽ đồ thị của các hàm số sau rồi lập bảng biến thiên của nó

Lựa chọn câu để xem lời giải nhanh hơn

Vẽ đồ thị của các hàm số sau rồi lập bảng biến thiên của nó

LG a

\(y = |{3 \over 2}x - 2|\)

Lời giải chi tiết:

Ta có: \(\frac{3}{2}x - 2 = 0 \Leftrightarrow x = \frac{4}{3}\)

Do đó \(y = \left\{ \matrix{
{3 \over 2}x - 2\,\,\,\,;x \ge {4 \over 3} \hfill \cr
- {3 \over 2} + 2\,\,\,\,;x < {4 \over 3} \hfill \cr} \right.\)

Đồ thị hàm số gồm hai phần:

+ Nửa đường thẳng \(y={3 \over 2}x - 2\) ứng với \(x \ge {4 \over 3}\).

+ Nưa đường thẳng \(y=-{3 \over 2}x + 2\) ứng với \(x < {4 \over 3}\).

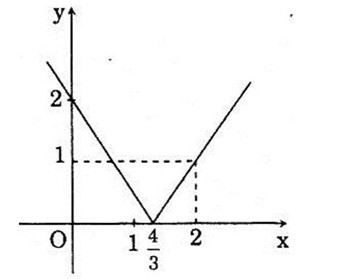
Bảng biến thiên:

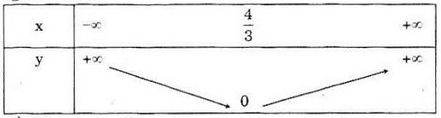
LG b

\(y = \left\{ \matrix{
2x\,\,\,\,\,\,\,\,\,\,\,\,\,\,;x < 0 \hfill \cr
{x^2} - x\,\,\,\,\,\,\,;x \ge 0 \hfill \cr} \right.\)

Lời giải chi tiết:

Đồ thị hàm số gồm hai phần:

+ Nửa đường thẳng y=2x ứng với \(x < 0\)

+ Nửa đường thẳng \(y={x^2} - x\) ứng với \(x \ge 0\)

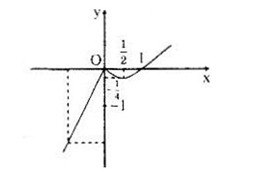
Bảng biến thiên:

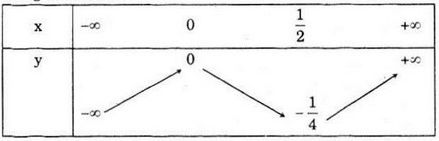
LG c

\(y = |{1 \over 2}{x^2} + x - {3 \over 2}|\)

Lời giải chi tiết:

Ta có:

\(y = \left\{ \matrix{
{1 \over 2}{x^2} + x - {3 \over 2}\,voi\,x \le - 3,x \ge - 1 \hfill \cr
- {1 \over 2}{x^2} - x + {3 \over 2}\,voi\, - 3 < x < 1 \hfill \cr} \right.\)

Do đó đồ thị cần vẽ là hợp của hai phần đồ thị:

+ Phần đồ thị hàm số \(y = \frac{1}{2}{x^2} + x - \frac{3}{2}\) nằm phía trên trục hoành.

+ Phần đồ thị hàm số \(y = \frac{1}{2}{x^2} + x - \frac{3}{2}\) phía dưới trục hoành được lấy đối xứng qua Ox.

Đồ thị hàm số:

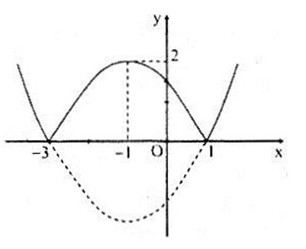
Bảng biến thiên:

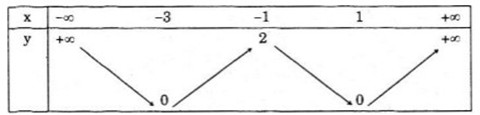
LG d

\(y = x|x| - 2x – 1\)

Lời giải chi tiết:

Ta có:

\(y = \left\{ \matrix{
{x^2} - 2x - 1\,\,\,\,\,;x \ge 0 \hfill \cr
-x^2-2x-1\,\,\,\,\,\,\,\,\,;x < 0 \hfill \cr} \right.\)

Đồ thị hàm số gồm hai phần:

+ Một phần parabol \(y={x^2} - 2x - 1\) ứng với \(x\ge 0\).

+ Một phần parabol \(y=-x^2-2x-1 \) ứng với \(x < 0\)

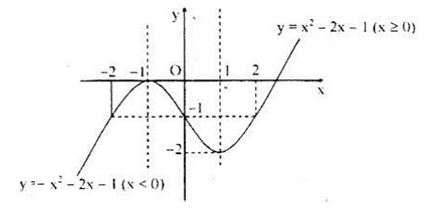
Bảng biến thiên:

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 8 phiếu

Bài tiếp theo

Bài 45 trang 64 SGK Đại số 10 nâng cao
Hãy nêu biểu thức xác định hàm số S(x).
Bài 46 trang 64 SGK Đại số 10 nâng cao
Theo lịch trình, để đến được Mặt Trăng, con tàu phải đi qua điểm (100; V) với y = 294 ± 1,5. Hỏi điều kiện đó có được thỏa mãn hay không?
Bài 43 trang 63 SGK Đại số 10 nâng cao
Lập bảng biến thiên và vẽ đồ thị của hàm số.
Bài 42 trang 63 SGK Đại số 10 nâng cao
Trong mỗi trường hợp cho dưới đây, hãy vẽ đồ thị hàm số của các hàm số trên cùng một hệ trục tọa độ rồi xác định tọa độ giao điểm của chúng.
Bài 41 trang 63 SGK Đại số 10 nâng cao
Dựa vào đồ thị của hàm số y = ax2 + bx + c. Hãy xác định dấu của các hệ số a, b và c trong mỗi trường hợp dưới đây:
Bài 40 trang 63 SGK Đại số 10 nâng cao
Tìm các hàm số chẵn trong các hàm số bậc hai y = ax2 + bx + c.
Bài 39 trang 63 SGK Đại số 10 nâng cao
Với mỗi câu sau đây. Hãy chọn phần kết luận mà em cho là đúng: