Bài 42 trang 63 SGK Đại số 10 nâng cao

Trong mỗi trường hợp cho dưới đây, hãy vẽ đồ thị hàm số của các hàm số trên cùng một hệ trục tọa độ rồi xác định tọa độ giao điểm của chúng.

Lựa chọn câu để xem lời giải nhanh hơn

Trong mỗi trường hợp cho dưới đây, hãy vẽ đồ thị hàm số của các hàm số trên cùng một hệ trục tọa độ rồi xác định tọa độ giao điểm của chúng.

LG a

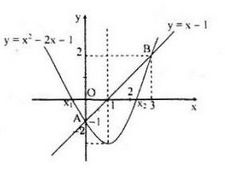
\(y = x - 1\) và \(y = x^2 - 2x - 1\)

Lời giải chi tiết:

Đường thẳng d: \(y = x – 1\) qua \(A(0; -1); B(1; 0)\)

Parabol (P): \(y = x^2– 2x – 1\) có đỉnh \(S(1; -2)\)

Phương trình hoành độ giao điểm của d và (P) là:

\(x^2 – 2x – 1 = x – 1 ⇔ x^2 - 3x = 0\)

\( \Leftrightarrow \left[ \matrix{
x = 0\,\,(y = - 1) \hfill \cr
x = 3\,\,(y = 2) \hfill \cr} \right.\)

Giao điểm của d và (P) là: \(A(0, -1)\) và \(C(3, 2)\)

LG b

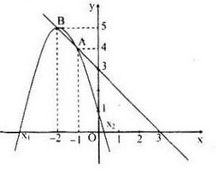
\(y = -x + 3\) và \(y = -x^2 - 4x + 1\)

Lời giải chi tiết:

Đường thẳng d: \(y = -x + 3\) qua \(A(0, 3); B(3, 0)\)

Parabol (P): \(y = -x^2 – 4x + 1\) có đỉnh \(S(-2, 5)\)

Phương trình hoành độ giao điểm của và (P) là:

\(\eqalign{
& - {x^2} - 4x + 1 = - x + 3 \cr
& \Leftrightarrow {x^2} + 3x + 2 = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = - 1\,\,\,\,(y = 4) \hfill \cr
x = - 2\,\,\,\,(y = 5) \hfill \cr} \right. \cr} \)

Giao điểm của d và (P) là \((-1, 4)\) và \((-2, 5)\)

LG c

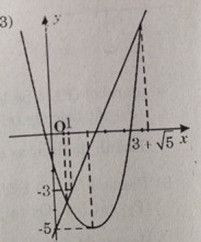
\(y = 2x - 5\) và \(y = x^2 - 4x - 1\)

Lời giải chi tiết:

Đường thẳng d: \(y = 2x – 5\) đi qua \(A(0, -5); B(1, -3)\)

Parabol (P): \(y = x^2 – 4x - 1\) có đỉnh \(S(2, -5)\)

Phương trình hoành độ giao điểm của và (P) là:

\(\eqalign{
& {x^2} - 4x - 1 = 2x - 5 \cr&\Leftrightarrow {x^2} - 6x + 4 = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = 3 - \sqrt 5 \,\,\,\,\,\,\,\,(y = 1 - 2\sqrt 5 ) \hfill \cr
x = 3 + \sqrt 5 \,\,\,\,\,\,\,\,\,(y = 1 + 2\sqrt 5 ) \hfill \cr} \right. \cr} \)

Giao điểm của (P) và d là: \((3 - \sqrt 5 ,\,1 - 2\sqrt 5 );\,(3 + \sqrt 5 ,\,1 + 2\sqrt 5 )\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 13 phiếu

Bài tiếp theo

Bài 43 trang 63 SGK Đại số 10 nâng cao
Lập bảng biến thiên và vẽ đồ thị của hàm số.
Bài 44 trang 64 SGK Đại số 10 nâng cao
Vẽ đồ thị của các hàm số sau rồi lập bảng biến thiên của nó
Bài 45 trang 64 SGK Đại số 10 nâng cao
Hãy nêu biểu thức xác định hàm số S(x).
Bài 46 trang 64 SGK Đại số 10 nâng cao
Theo lịch trình, để đến được Mặt Trăng, con tàu phải đi qua điểm (100; V) với y = 294 ± 1,5. Hỏi điều kiện đó có được thỏa mãn hay không?
Bài 41 trang 63 SGK Đại số 10 nâng cao
Dựa vào đồ thị của hàm số y = ax2 + bx + c. Hãy xác định dấu của các hệ số a, b và c trong mỗi trường hợp dưới đây:
Bài 40 trang 63 SGK Đại số 10 nâng cao
Tìm các hàm số chẵn trong các hàm số bậc hai y = ax2 + bx + c.
Bài 39 trang 63 SGK Đại số 10 nâng cao
Với mỗi câu sau đây. Hãy chọn phần kết luận mà em cho là đúng: