Bài 33 trang 103 SGK Hình học 10 Nâng cao
Tính độ dài dây cung của (E) đi qua một tiêu điểm và vuông góc với trục tiêu
Cho elip \((E):{{{x^2}} \over 9} + {{{y^2}} \over 1} = 1.\)
LG a
Tính độ dài dây cung của (E) đi qua một tiêu điểm và vuông góc với trục tiêu (đoạn thẳng nối hai điểm của elip gọi là dây cung của elip, trục chứa các tiêu điểm gọi là trục tiêu của elip).
Lời giải chi tiết:
+ Ta có: \({a^2} = 9,{b^2} = 1 \) \(\Rightarrow {c^2} = {a^2} - {b^2} = 9 - 1 = 8 \)
\(\Rightarrow c = 2\sqrt 2 \)
\(\Rightarrow {F_1}\left( { - 2\sqrt 2 ;0} \right);\,{F_2}\left( {2\sqrt 2 ;0} \right)\)
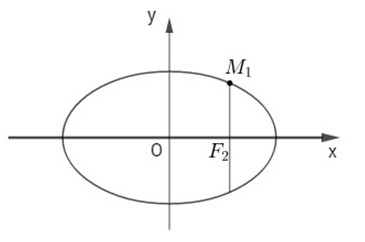
Đường thẳng đi qua tiêu điểm \(F_2\) và vuông góc trục tiêu có phương trình \(x = 2\sqrt 2 \)
Tọa độ giao điểm của đường thẳng với (E) thỏa mãn hệ phương trình:
\( \left\{ \begin{array}{l}
x = 2\sqrt 2 \,\,\,\,\,\,\,\,\left( 1 \right)\\
\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\,\,\left( 2 \right)
\end{array} \right.\)
Thay (1) và (2) ta được:
\({8 \over 9} + {{{y^2}} \over 1} = 1 \Leftrightarrow {y^2} = {1 \over 9} \Leftrightarrow y = \pm {1 \over 3}.\)
Vậy \({M_1}\left( {2\sqrt 2 ;{1 \over 3}} \right);{M_2}\left( {2\sqrt 2 ; - {1 \over 3}} \right)\) và độ dài dây cung cần tìm là:
\({M_1}{M_2} \) \(= \sqrt {{{\left( {2\sqrt 2 - 2\sqrt 2 } \right)}^2} + {{\left( { - \frac{1}{3} - \frac{1}{3}} \right)}^2}} \) \( = \sqrt {0 + \frac{4}{3}} = \frac{2}{3}\)
LG b
Tìm trên (E) điểm M sao cho \(M{F_1} = 2M{F_2}\) , trong đó \({F_1},{F_2}\) lần lượt là các tiêu điểm của (E) nằm bên trái và bên phải trục tung.
Phương pháp giải:
Sử sụng công thức tính bán kính qua tiêu: \(M{F_1} = a + \frac{c}{a}x,M{F_2} = a - \frac{c}{a}x\)
Lời giải chi tiết:
Ta có:
\(\eqalign{
& M{F_1} = a + {c \over a}x = 3 + {{2\sqrt 2 } \over 3}x \cr
& M{F_2} = a - {c \over a}x = 3 - {{2\sqrt 2 } \over 3}x \cr
& M{F_1} = 2M{F_2}\cr & \Leftrightarrow 3 + {{2\sqrt 2 } \over 3}x = 6 - {{4\sqrt 2 } \over 3}x \cr&\Leftrightarrow 2\sqrt 2 x = 3 \Leftrightarrow x = {{3\sqrt 2 } \over 4}. \cr} \)
Thay \(x = {{3\sqrt 2 } \over 4}\) vào phương trình elip ta được:
\({2 \over {16}} + {y^2} = 1 \Leftrightarrow {y^2} = {7 \over 8} \Leftrightarrow y = \pm {{\sqrt {14} } \over 4}.\)
Vậy \({M_1}\left( {{{3\sqrt 2 } \over 4};{{\sqrt {14} } \over 4}} \right);{M_2}\left( {{{3\sqrt 2 } \over 4}; - {{\sqrt {14} } \over 4}} \right).\)
Loigiaihay.com













Danh sách bình luận