Bài 27 trang 24 SGK Hình học 10 Nâng cao

Đề bài

Cho lục giác ABCDEF. Gọi P, Q, R, S, T, U lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác PRT và QSU có trọng tâm trùng nhau.

Lời giải chi tiết

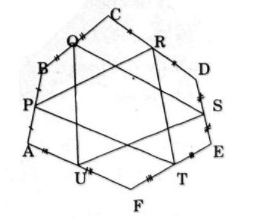
Lấy $O$ bất kì và gọi $K, G$ lần lượt là trọng tâm tam giác $PRT$ và $QSU$, ta có

$\eqalign{ & 3\overrightarrow {OG} \cr&= \overrightarrow {OP} + \overrightarrow {OR} + \overrightarrow {OT} \cr&= {1 \over 2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + {1 \over 2}\left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) + {1 \over 2}\left( {\overrightarrow {OE} + \overrightarrow {OF} } \right) \cr  & = {1 \over 2}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} + \overrightarrow {OF} } \right)\,\,\,(1) \cr  & 3\overrightarrow {OK} \cr&= \overrightarrow {OQ} + \overrightarrow {OS} + \overrightarrow {OU}\cr&  = {1 \over 2}\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right) + {1 \over 2}\left( {\overrightarrow {OD} + \overrightarrow {OE} } \right) + {1 \over 2}\left( {\overrightarrow {OA} + \overrightarrow {OF} } \right) \cr  & = {1 \over 2}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} + \overrightarrow {OF} } \right)\,\,\,\,(2) \cr}$

Từ (1) và (2) suy ra  $\overrightarrow {OG}  = \overrightarrow {OK}$ hay $G \equiv K.$

Vậy hai tam giác $PRT$ và $QSU$ có trọng tâm trùng nhau.

Cách khác:

Sử dụng kết quả bài 26, để chứng minh hai tam giác PRT và QSU có cùng trọng tâm, ta chứng minh $\overrightarrow {PQ}  + \overrightarrow {RS}  + \overrightarrow {TU}  = \overrightarrow 0$

Do Q là trung điểm BC nên:

$\begin{array}{l} \overrightarrow {PQ} = \dfrac{1}{2}\left( {\overrightarrow {PB} + \overrightarrow {PC} } \right) \\= \dfrac{1}{2}\left( { - \overrightarrow {PA} + \overrightarrow {PC} } \right)\\ = \dfrac{1}{2}\left( {\overrightarrow {PC} - \overrightarrow {PA} } \right) = \dfrac{1}{2}\overrightarrow {AC} \end{array}$

Do S là trung điểm DE nên:

$\begin{array}{l} \overrightarrow {RS} = \dfrac{1}{2}\left( {\overrightarrow {RD} + \overrightarrow {RE} } \right)\\ = \dfrac{1}{2}\left( { - \overrightarrow {RC} + \overrightarrow {RE} } \right)\\ = \dfrac{1}{2}\left( {\overrightarrow {RE} - \overrightarrow {RC} } \right) = \dfrac{1}{2}\overrightarrow {CE} \end{array}$

Do U là trung điểm FA nên:

$\begin{array}{l} \overrightarrow {TU} = \dfrac{1}{2}\left( {\overrightarrow {TF} + \overrightarrow {TA} } \right) \\= \dfrac{1}{2}\left( { - \overrightarrow {TE} + \overrightarrow {TA} } \right)\\ = \dfrac{1}{2}\left( {\overrightarrow {TA} - \overrightarrow {TE} } \right) = \dfrac{1}{2}\overrightarrow {EA} \end{array}$

Do đó,

$\begin{array}{l} \overrightarrow {PQ} + \overrightarrow {RS} + \overrightarrow {TU} \\ = \dfrac{1}{2}\overrightarrow {AC} + \dfrac{1}{2}\overrightarrow {CE} + \dfrac{1}{2}\overrightarrow {EA} \\ = \dfrac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} } \right)\\ = \dfrac{1}{2}\left( {\overrightarrow {AE} + \overrightarrow {EA} } \right)\\ = \dfrac{1}{2}\overrightarrow {AA} \\ = \overrightarrow 0 \end{array}$

Vậy hai tam giác có cùng trọng tâm.

Loigiaihay.com