Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học Bài 4. Tích của một vectơ với một số

Bài 25 trang 24 Sách giáo khoa (SGK) Hình học 10 Nâng cao


Gọi G là trọng tâm tam giác ABC.

Đề bài

Gọi \(G\) là trọng tâm tam giác \(ABC\). Đặt \(\overrightarrow a  = \overrightarrow {GA} \) và \(\overrightarrow b  = \overrightarrow {GB} \). Hãy biểu thị mỗi vec tơ \(\overrightarrow {AB} ,\overrightarrow {GC} ,\overrightarrow {BC} ,\overrightarrow {CA} \) qua các vec tơ \(\overrightarrow a \) và \(\overrightarrow b \).

Lời giải chi tiết

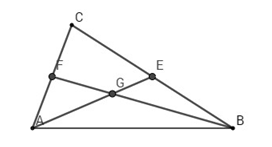
Vì \(G\) là trọng tâm tam giác \(ABC\) nên \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Ta có

\(\eqalign{
& \overrightarrow {AB} = \overrightarrow {GB} - \overrightarrow {GA} = \overrightarrow b - \overrightarrow a \cr 
& \overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0\cr&=>\overrightarrow {GC} = - \overrightarrow {GB} - \overrightarrow {GA} = - \overrightarrow b - \overrightarrow a \cr 
& \overrightarrow {BC} = \overrightarrow {GC} - \overrightarrow {GB} = - \overrightarrow b - \overrightarrow a - \overrightarrow b \cr&= - 2\overrightarrow b - \overrightarrow a \cr 
& \overrightarrow {CA} = \overrightarrow {GA} - \overrightarrow {GC} \cr&= \overrightarrow a - \left( { - \overrightarrow b - \overrightarrow a } \right) \cr&= 2\overrightarrow a + \overrightarrow b \cr} \)

Loigiaihay.com


Bình chọn:
3.2 trên 13 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store