Bài 13 trang 15 Sách giáo khoa (SGK) Hình học 10 Nâng cao

Cho hai lực ...

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

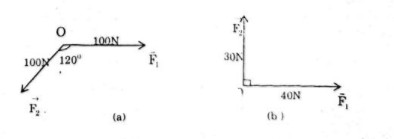
Cho hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) cùng có điểm đặt tại \(O\) (h.17). Tìm cường độ lực tổng hợp của chúng trong các trường hợp sau

LG a

\(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đều có cường độ là \(100N\), góc hợp bởi \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng \({120^0}\) (h.17a)

Phương pháp giải:

- Sử dụng quy tắc hình bình hành dựng véc tơ tổng hợp lực.

- Sử dụng kiến thức hình học phẳng tính độ dài đoạn thẳng.

Lời giải chi tiết:

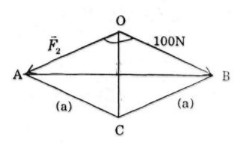
Ta lấy \(\overrightarrow {{F_2}} = \overrightarrow {OA} ,\,\overrightarrow {{F_1}} = \overrightarrow {OB} \).

Theo quy tắc hình bình hành, ta vẽ hình bình hành \(OACB\).

Hình bình hành \(OACB\) có \(OA = OB\) nên \(OACB\) là hình thoi.

Ta có \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \), \(OC\) là phân giác góc \(\widehat {AOB}\) nên \(\widehat {AOC} = {60^0}\).

Mà \(OACB\) là hình thoi nên OA=AC hay tam giác \(AOC\) đều.

Suy ra \(OA = OC\).

Vậy cường độ lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là \(100N\).

LG b

Cường độ của \(\overrightarrow {{F_1}} \) là \(40N\), của \(\overrightarrow {{F_2}} \) là \(30N\) và góc giữa \(\overrightarrow {{F_1}} \) và \( \overrightarrow {{F_2}} \) bằng \(90^0\)(h.17b)

Lời giải chi tiết:

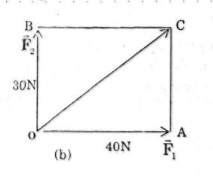
Đặt \(\overrightarrow {OA} = \overrightarrow {{F_1}} ,\overrightarrow {OB} = \overrightarrow {{F_2}} \). \(C\) là đỉnh thứ tư của hình bình hành \(OACB\).

Do góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng \({90^0}\) suy ra tứ giác \(OACB\) là hình chữ nhật.

Ta có: \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)

Theo pitago trong tam giác OAC có:

\(OC = \sqrt {O{A^2} + A{C^2}} = \sqrt {O{A^2} + O{B^2}}\)

\( = \sqrt {{{40}^2} + {{30}^2}} \) \( = 50N\)

Vậy cường độ tổng hợp lực của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là \(50N.\)

Loigiaihay.com