 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 Bài 2. Tổng của hai vectơ
Bài 2. Tổng của hai vectơ
Bài 11 trang 14 sách giáo khoa (SGK) Hình học 10 Nâng cao
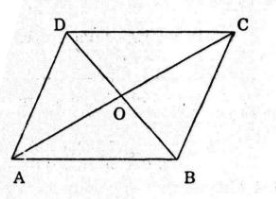
Cho hình bình hành ABCD với tâm O. Mỗi khẳng định sau đây đúng hay sai ?
Cho hình bình hành \(ABCD\) với tâm \(O\). Mỗi khẳng định sau đây đúng hay sai ?
LG a
\(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {BD} } \right|\);
Phương pháp giải:
Sử dụng quy tắc ba điểm, quy tắc hình bình hành:
Với ba điểm M, N, P bất kì ta có: \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \)
Nếu OABC là hình bình hành thì ta có:
\(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} \)
Lời giải chi tiết:
Sai vì \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right|\) thì chưa chắc \(AC, BD\) đã bằng nhau do \(ABCD\) là hình bình hành.
LG b
\(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {BC} \)
Lời giải chi tiết:
Đúng vì \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {BC} \)
LG c
\(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \)
Lời giải chi tiết:
Sai vì:
\(\overrightarrow {OA} + \overrightarrow {OB} \)
\(= \left( {\overrightarrow {OC} + \overrightarrow {CA} } \right) + \left( {\overrightarrow {OD} + \overrightarrow {DB} } \right) \)
\(= \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {CA} + \overrightarrow {DB} } \right)\)
\(\ne \overrightarrow {OC} + \overrightarrow {OD} \)
LG d
\(\overrightarrow {BD} + \overrightarrow {AC} = \overrightarrow {AD} + \overrightarrow {BC} \).
Lời giải chi tiết:
Đúng vì \(\overrightarrow {BD} + \overrightarrow {AC} \)
\(= \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {DC} } \right) \)
\(= \left( {\overrightarrow {DC} + \overrightarrow {CD} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {AD} } \right) \)
\( = \overrightarrow {DD} + \left( {\overrightarrow {BC} + \overrightarrow {AD} } \right)\)
\(= \overrightarrow {AD} + \overrightarrow {BC} \)
Loigiaihay.com












Danh sách bình luận