Bài 1 trang 63 SGK Hình học 12 Nâng cao

Cho mp(P) và điểm A không thuộc (P). Chứng minh rằng mọi mặt cầu đi qua A và có tâm nằm trên (P) luôn luôn đi qua hai điểm cố định.

Đề bài

Cho mp \((P)\) và điểm \(A\) không thuộc \((P)\). Chứng minh rằng mọi mặt cầu đi qua \(A\) và có tâm nằm trên \((P)\) luôn luôn đi qua hai điểm cố định.

Lời giải chi tiết

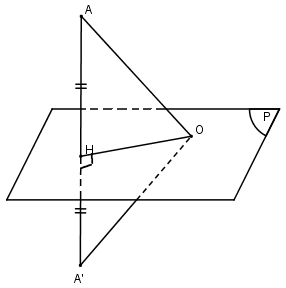
Lấy điểm \(O\) nằm trên mp \((P)\). Gọi \((S)\) là mặt cầu đi qua \(A\) có tâm \(O\).

Gọi \(A’\) là điểm đối xứng của \(A\) qua mp \((P)\) ta có \(OA’ = OA = R\) nên \((S)\) đi qua \(A’\). Vậy mặt cầu \((S)\) luôn đi qua hai điểm cố định \(A\) và \(A’\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4 trên 7 phiếu

Bài tiếp theo

Bài 2 trang 63 SGK Hình học 12 Nâng cao
Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp S.ABC
Bài 3 trang 63 SGK Hình học 12 Nâng cao
Cho hai đường tròn (O; r) và (O’; r’) cắt nhau tại hai điểm A, B và lần lượt nằm trên hai mặt phẳng phân biệt (P) và (P’).
Bài 4 trang 63 SGK Hình học 12 Nâng cao
Cho hình nón (N) sinh bởi tam giác đều cạnh a khi quay quanh một đường cao của tam giác đó. a) Một mặt cầu có diện tích bằng diện tích toàn phần của hình nón (N) thì có bán kính bằng bao nhiêu? b) Một khối cầu có thể tích của khối nón (N) thì có bán kính bằng bao nhiêu?
Bài 5 trang 63 Hình học 12 Nâng cao
Cho tam giác ABC vuông tại A, . Gọi là thể tích các khối tròn xoay sinh bởi tam giác đó (kê cả các điểm trong) khi lần lượt quay quanh AB, AC, BC.
Bài 6 trang 63 Hình học 12 Nâng cao
Một hình thang cân ABCD có các cạnh đáy AB = 2a, BD = 4a, cạnh bên AD = BC = 3a. Hãy tính thể tích và diện tích toàn phần của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của nó.
Câu hỏi 2 trang 62 SGK Hình Học 12 nâng cao
Trả lời câu hỏi 2 trang 62 sách giáo khoa Hình Học 12 nâng cao. Trong các mệnh đề sau đây, mệnh đề nào đúng?
Câu hỏi 1 trang 62 SGK Hình Học 12 nâng cao
Trả lời câu hỏi 1 trang 62 sách giáo khoa Hình Học 12 nâng cao. Trong các mệnh đề sau đây, mệnh đề nào đúng? a) Mặt cầu, khối cầu đều có vô số mặt phẳng đối xứng. b) Mọi tứ diện luôn có cạnh bên bằng nhau đều có mặt cầu ngoại tiếp.