Bài tập trắc nghiệm Toán 6 - Chân trời sáng tạo có đáp án Bài tập trắc nghiệm Chương 9. Một số yếu tố xác suất

Trắc nghiệm Bài tập ôn tập chương 9: Một số yếu tố thống kê Toán 6 Chân trời sáng tạo

Làm bài tập

Đề bài

Câu 1 :

Trong hộp có 10 lá thư có bì thư giống nhau, bên trong mỗi bì thư có 1 lá thư và được đánh số từ 1 đến 10. Mỗi bạn lấy ngẫu nhiên một bì thư, xem số ghi trên lá thư rồi trả lại vào bì và cho vào hộp. Sự kiện có thể xảy ra là

A.

Số ghi trên lá thư là số 11
B.

Số ghi trên lá thư là số 5
C.

Số ghi trên lá thư là số nhỏ hơn 1
D.

Số ghi trên lá thư là số lớn hơn 13

Câu 2 :

Trong một hộp có 1 quả bóng xanh và 9 bóng vàng có kích thước giống nhau. An lấy ra đồng thời 2 bóng từ hộp. Có các sự kiện sau:

1- An lấy được 2 bóng màu xanh

2- An lấy được ít nhất một bóng màu vàng

3- An lấy được 2 bóng màu vàng.

Sự kiện chắc chắn, không thể và có thể xảy ra lần lượt là

A.

1-2-3
B.

2-3-1
C.

3-2-1
D.

2-1-3

Câu 3 :

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.

Số xuất hiện trên thẻ được rút có phải là phần tử của tập hợp {1;2;3;4;5} hay không?

Không

Có

Câu 4 :

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.

Viết tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

A.

M={1;2;3;4}
B.

M={1,2,3,4,5}
C.

M={1,2,3,4}
D.

M={1;2;3;4;5}

Câu 5 :

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.

Hai điều cần chú ý trong mô hình xác suất của trò chơi trên là

1. Rút ngẫu nhiên

$?$

thẻ;

2. Tập hợp các kết quả có thể xảy ra đối với

$?$

xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1, 2, 3, 4, 5 là các số xuất hiện trên thẻ.

Câu 6 :

Cho phép thử nghiệm gieo con xúc xắc 6 mặt. Sự kiện nào trong các sự kiện sau có thể xảy ra:

A.

“Số chấm nhỏ hơn 5”
B.

“Số chấm lớn hơn 6”
C.

“Số chấm bằng 0”
D.

“Số chấm bằng 7”

Câu 7 :

Phép thử nghiệm: Bạn Ngô chọn một ngày trong tuần để đá bóng. Có tất cả bao nhiêu kết quả có thể xảy ra của phép thử nghiệm này.

A.

5
B.

6
C.

7
D.

4

Câu 8 :

Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:

Mặt	1 chấm	2 chấm	3 chấm	4 chấm	5 chấm	6 chấm
Số lần	8	7	3	12	10	10

Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.

A.

0,21
B.

0,44
C.

0,42
D.

0,18

Hằng ngày Sơn đều đi xe buýt đến trường. Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:

Câu 9

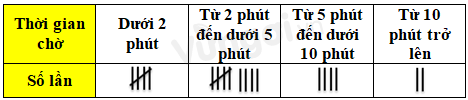
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút”

A.

0,2
B.

5
C.

0,5
D.

0,25

Câu 10

Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên”

A.

0,3
B.

6
C.

0,6
D.

0,2

Câu 11

Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút”

A.

0,1
B.

0,2
C.

0,9
D.

0,5

Trong hộp có một số bút xanh, một số bút vàng và một số bút đỏ. lấy ngẫu nhiên 1 bút từ hộp, xem màu gì rồi trả lại. Lặp lại hoạt động trên 40 lần ta được kết quả như sau:

Màu bút	Bút xanh	Bút vàng	Bút đỏ
Số lần	14	10	16

Câu 12

Tính xác suất thực nghiệm của sự kiện lấy được màu đỏ

A.

0,16
B.

0,6
C.

0,4
D.

0,45

Câu 13

Tính xác suất thực nghiệm của sự kiện không lấy được màu vàng

A.

0,25
B.

0,75
C.

0,1
D.

0,9

Tung đồng xu 15 lần liên tiếp và kết quả thu được ghi lại trong bảng sau:

Lần tung	Kết quả	Lần tung	Kết quả	Lần tung	Kết quả
1	S	6	N	11	N
2	S	7	S	12	S
3	N	8	S	13	N
4	S	9	N	14	N
5	N	10	N	15	N

N: Ngửa

S: Sấp

Câu 14

Số lần xuất hiện mặt ngửa (N) là

A.

6
B.

7
C.

8
D.

9

Câu 15

Xác suất thực nghiệm xuất hiện mặt ngửa là

A.

0,9
B.

0,6
C.

0,4
D.

0,7

Câu 16

Xác suất thực nghiệm xuất hiện mặt S là

A.

0,9
B.

0,6
C.

0,4
D.

0,7

Tổng hợp kết quả xét nghiệm bệnh viêm gan ở một phòng khám trong một năm ta được bảng sau:

Quý	Số ca xét nghiệm	Số ca dương tính
I	210	21
II	150	15
III	180	9
IV	240	48

Câu 17

Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là

A.

$0,05$
B.

$0,15$
C.

$\dfrac{1}{{12}}$
D.

$\dfrac{1}{{15}}$

Câu 18

Có bao nhiêu quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1?

A.

1
B.

2
C.

3
D.

0

Câu 19

Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là

A.

0,1
B.

0,25
C.

0,15
D.

0,125

Câu 20 :

Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?

A.

$\dfrac{7}{{11}}$
B.

$\dfrac{4}{{11}}$
C.

$\dfrac{4}{7}$
D.

$\dfrac{3}{7}$

Lời giải và đáp án

Câu 1 :

A.

Số ghi trên lá thư là số 11
B.

Số ghi trên lá thư là số 5
C.

Số ghi trên lá thư là số nhỏ hơn 1
D.

Số ghi trên lá thư là số lớn hơn 13

Đáp án : B

Phương pháp giải :

Tìm tất cả các kết quả có thể xảy ra khi lấy ngẫu nhiên.

Kiểm tra các sự kiện có thể xuất hiện trong tất cả các kết quả trên hay không

Lời giải chi tiết :

Các số có thể ghi trên lá thư là 1;2;3;4;5;6;7;8;9;10.

Trong 10 khả năng trên có số 5 nên số 5 có thể xuất hiện trên lá thư.

Vậy sự kiện “Số ghi trên lá thư là số 5” là sự kiện có thể xảy ra.

Câu 2 :

Trong một hộp có 1 quả bóng xanh và 9 bóng vàng có kích thước giống nhau. An lấy ra đồng thời 2 bóng từ hộp. Có các sự kiện sau:

1- An lấy được 2 bóng màu xanh

2- An lấy được ít nhất một bóng màu vàng

3- An lấy được 2 bóng màu vàng.

Sự kiện chắc chắn, không thể và có thể xảy ra lần lượt là

A.

1-2-3
B.

2-3-1
C.

3-2-1
D.

2-1-3

Đáp án : D

Phương pháp giải :

Tìm tất cả các kết quả có thể xảy ra trong mỗi lần lấy bóng.

Sự kiện chắc chắn xảy ra: Luôn xảy ra.

Sự kiện không thể xảy ra: Không bao giờ xảy ra

Sự kiện có thể xảy ra: Lúc xảy ra, lúc không xảy ra.

Lời giải chi tiết :

Các kết quả có thể xảy ra là: (1 xanh + 1 vàng) ; (2 vàng).

Cả hai kết quả này luôn có xuất hiện quả màu vàng nên sự kiện 2 chắc chắn xảy ra.

Ta không bao giờ có thể lấy được 2 quả bóng màu xanh cùng một lúc được vì tổng số bóng xanh chỉ có 1 quả. Sự kiện 1 là sự kiện không thể xảy ra.

Trong hai kết quả trên có một kết quả là 2 vàng nên sự kiện 3 có thể xảy ra.

Vậy sự kiện chắc chắn, không thể và có thể xảy ra lần lượt là 2-1-3.

Câu 3 :

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.

Số xuất hiện trên thẻ được rút có phải là phần tử của tập hợp {1;2;3;4;5} hay không?

Không

Có

Đáp án

Có

Phương pháp giải :

- Tìm các kết quả có thể xảy ra.

- Số có trong tập hợp là phần tử của tập hợp.

Lời giải chi tiết :

Số có thể xuất hiện trên thẻ là một trong năm số: 1;2;3;4;5.

Các số này đều là phần tử của tập hợp {1;2;3;4;5}.

Câu 4 :

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.

Viết tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

A.

M={1;2;3;4}
B.

M={1,2,3,4,5}
C.

M={1,2,3,4}
D.

M={1;2;3;4;5}

Đáp án : D

Phương pháp giải :

- Tìm các kết quả có thể xảy ra.

- Viết tập hợp: Viết các số trong dấu ngoặc kép { }.

Lời giải chi tiết :

Số có thể xuất hiện trên thẻ là một trong năm số: 1;2;3;4;5.

Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ là

M={1;2;3;4;5}.

Câu 5 :

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ.

Hai điều cần chú ý trong mô hình xác suất của trò chơi trên là

1. Rút ngẫu nhiên

$?$

thẻ;

2. Tập hợp các kết quả có thể xảy ra đối với

$?$

xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1, 2, 3, 4, 5 là các số xuất hiện trên thẻ.

Đáp án

1. Rút ngẫu nhiên

$1||một$

thẻ;

2. Tập hợp các kết quả có thể xảy ra đối với

$số$

xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1, 2, 3, 4, 5 là các số xuất hiện trên thẻ.

Lời giải chi tiết :

Hai điều cần chú ý trong mô hình xác suất của trò chơi trên là

1. Rút ngẫu nhiên 1 thẻ;

2. Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ là {1,2,3,4,5}. Ở đây, 1,2,3,4,5 là các số xuất hiện trên thẻ.

Câu 6 :

Cho phép thử nghiệm gieo con xúc xắc 6 mặt. Sự kiện nào trong các sự kiện sau có thể xảy ra:

A.

“Số chấm nhỏ hơn 5”
B.

“Số chấm lớn hơn 6”
C.

“Số chấm bằng 0”
D.

“Số chấm bằng 7”

Đáp án : A

Phương pháp giải :

Tìm tất các kết quả có thể xảy ra khi gieo xúc xắc.

Kiểm tra sự kiện có thể nằm trong các kết quả đó không.

Lời giải chi tiết :

Các kết quả có thể xảy ra khi gieo một con xúc xắc 6 mặt là: 1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm.

Khi đó số chấm nhỏ hơn 5 có thể xảy ra. Đáp án A đúng.

Số chấm tối đa là 6 nên B sai.

Không có số chấm bằng 0 trong các kết quả có thể xảy ra nên C sai.

Không có số chấm bằng 7 trong các kết quả có thể xảy ra nên D sai.

Câu 7 :

Phép thử nghiệm: Bạn Ngô chọn một ngày trong tuần để đá bóng. Có tất cả bao nhiêu kết quả có thể xảy ra của phép thử nghiệm này.

A.

5
B.

6
C.

7
D.

4

Đáp án : C

Phương pháp giải :

Liệt kê các ngày trong tuần mà Ngô có thể chọn.

Đếm số ngày.

Lời giải chi tiết :

Một tuần có 7 ngày nên Ngô có thể chọn một trong 7 ngày đó để đi đá bóng. Hay số kết quả có thể xảy ra là 7.

Câu 8 :

Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:

Mặt	1 chấm	2 chấm	3 chấm	4 chấm	5 chấm	6 chấm
Số lần	8	7	3	12	10	10

Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.

A.

0,21
B.

0,44
C.

0,42
D.

0,18

Đáp án : C

Phương pháp giải :

- Xác định các mặt có số lẻ chấm

- Tìm trên bảng số lần xuất hiện của các mặt đó.

- Tính xác suất thực nghiệm:

Lời giải chi tiết :

Tổng số lần gieo là 50.

Các mặt có số lẻ chấm của con xúc xắc là mặt 1, 3 và 5.

Số lần được mặt 1 chấm là 8 lần, mặt 3 chấm là 3 lần, mặt 5 chấm là 10 lần.

Số lần được mặt có số lẻ chấm là 8+3+10=21 lần

Xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần là:

$\dfrac{{21}}{{50}} = 0,42$

Hằng ngày Sơn đều đi xe buýt đến trường. Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:

Câu 9

Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút”

A.

0,2
B.

5
C.

0,5
D.

0,25

Đáp án: D

Phương pháp giải :

- Một gạch là 1 lần (Tính cả gạch chéo).

- Xác định số lần Sơn phải chờ xe dưới 2 phút.

- Tính xác suất:

Lời giải chi tiết :

Tổng số lần Sơn chờ xe là 20 lần.

Số lần Sơn phải chờ xe dưới 2 phút là 5 lần.

Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 2 phút” là:

$\dfrac{5}{{20}} = 0,25$

Câu 10

Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên”

A.

0,3
B.

6
C.

0,6
D.

0,2

Đáp án: A

Phương pháp giải :

- Xác định số lần Sơn phải chờ xe từ 5 phút trở lên: Từ 5 phút đến dưới 10 phút + Từ 10 phút trở lên.

- Tính xác suất:

Lời giải chi tiết :

Tổng số lần Sơn chờ xe là 20 lần.

Số lần Sơn phải chờ xe từ 5 phút đến dưới 10 phút là: 4 lần

Số lần Sơn phải chờ xe từ 10 phút trở lên là: 2 lần

Số lần Sơn phải chờ xe từ 5 phút trở lên là: 4+2 = 6 lần.

Xác suất của sự kiện “Sơn phải chờ xe từ 5 phút trở lên” là:

$\dfrac{6}{{20}} = 0,3$

Câu 11

Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút”

A.

0,1
B.

0,2
C.

0,9
D.

0,5

Đáp án: C

Phương pháp giải :

- Xác định số lần Sơn phải chờ xe dưới 10 phút: dưới 2 phút + Từ 2 đến dưới 5 phút + Từ 5 phút đến dưới 10 phút .

- Tính xác suất:

Lời giải chi tiết :

Tổng số lần Sơn chờ xe là 20 lần.

Số lần Sơn phải chờ xe dưới 2 phút là 5 lần.

Số lần Sơn phải chờ xe từ 2 phút đến dưới 5 phút là 9 lần.

Số lần Sơn phải chờ xe từ 5 phút đến dưới 10 phút là 4 lần.

Số lần Sơn phải chờ xe dưới 10 phút là 5+9+4=18 lần.

Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút” là:

$\dfrac{{18}}{{20}} = 0,9$

Màu bút	Bút xanh	Bút vàng	Bút đỏ
Số lần	14	10	16

Câu 12

Tính xác suất thực nghiệm của sự kiện lấy được màu đỏ

A.

0,16
B.

0,6
C.

0,4
D.

0,45

Đáp án: C

Phương pháp giải :

- Xác định số lần lấy được màu đỏ.

- Tính xác suất thực nghiệm=Số lần lấy được màu đỏ:40

Lời giải chi tiết :

Tổng số lần lấy là 40.

Số lần lấy được màu đỏ là 16.

Xác suất thực nghiệm của sự kiện lấy được màu đỏ là:

$\dfrac{{16}}{{40}} = 0,4$

Câu 13

Tính xác suất thực nghiệm của sự kiện không lấy được màu vàng

A.

0,25
B.

0,75
C.

0,1
D.

0,9

Đáp án: B

Phương pháp giải :

- Xác định số lần lấy được màu vàng.

- Xác định số lần không lấy được màu vàng.

- Tính xác suất thực nghiệm=Số lần không lấy được màu vàng:40

Lời giải chi tiết :

Tổng số lần lấy bút là 40.

Số lần lấy được màu vàng là 10

Số lần không lấy được màu vàng là 40-10=30.

Xác suất suất thực nghiệm của sự kiện không lấy được màu vàng là:

$\dfrac{{30}}{{40}} = 0,75$

Tung đồng xu 15 lần liên tiếp và kết quả thu được ghi lại trong bảng sau:

Lần tung	Kết quả	Lần tung	Kết quả	Lần tung	Kết quả
1	S	6	N	11	N
2	S	7	S	12	S
3	N	8	S	13	N
4	S	9	N	14	N
5	N	10	N	15	N

N: Ngửa

S: Sấp

Câu 14

Số lần xuất hiện mặt ngửa (N) là

A.

6
B.

7
C.

8
D.

9

Đáp án: D

Phương pháp giải :

Xác suất thực nghiệm trong trò chơi tung đồng xu

Lời giải chi tiết :

Số lần xuất hiện mặt ngửa là 9 lần.

Câu 15

Xác suất thực nghiệm xuất hiện mặt ngửa là

A.

0,9
B.

0,6
C.

0,4
D.

0,7

Đáp án: B

Phương pháp giải :

- Xác định số lần xuất hiện mặt ngửa.

- Xác suất thực nghiệm=Số lần được N: Tổng số lần tung.

Lời giải chi tiết :

Tổng số lần tung là 15 lần

Số lần xuất hiện mặt N là 9 lần.

Xác suất thực nghiệm xuất hiện mặt ngửa là $\dfrac{9}{{15}} = \dfrac{3}{5} = 0,6$

Câu 16

Xác suất thực nghiệm xuất hiện mặt S là

A.

0,9
B.

0,6
C.

0,4
D.

0,7

Đáp án: C

Phương pháp giải :

- Xác định số lần xuất hiện mặt sấp.

- Xác suất thực nghiệm=Số lần được S: Tổng số lần tung.

Lời giải chi tiết :

Tổng số lần tung là 15 lần

Số lần xuất hiện mặt S là 15-9=6 lần.

Xác suất thực nghiệm xuất hiện mặt ngửa là $\dfrac{6}{{15}} = \dfrac{2}{5} = 0,4$

Tổng hợp kết quả xét nghiệm bệnh viêm gan ở một phòng khám trong một năm ta được bảng sau:

Quý	Số ca xét nghiệm	Số ca dương tính
I	210	21
II	150	15
III	180	9
IV	240	48

Câu 17

Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là

A.

$0,05$
B.

$0,15$
C.

$\dfrac{1}{{12}}$
D.

$\dfrac{1}{{15}}$

Đáp án: C

Phương pháp giải :

- Tính số ca xét nghiệm sau quý III tính từ đầu năm.

- Tính số ca dương tính sau quý III tính từ đầu năm.

- Xác suất thực nghiệm=Số ca dương tính: Số ca xét nghiệm.

Lời giải chi tiết :

Số ca xét nghiệm sau quý III tính từ đầu năm là 210+150+180=540.

Số ca dương tính sau quý III tính từ đầu năm là 21+15+9=45.

Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính sau quý III tính từ đầu năm” là $\dfrac{{45}}{{540}} = \dfrac{1}{{12}}$

Câu 18

Có bao nhiêu quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1?

A.

1
B.

2
C.

3
D.

0

Đáp án: A

Phương pháp giải :

Bước 1: Tính xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của từng quý:

- Xác định số ca dương tính quý I, II, III, IV.

- Xác suất thực nghiệm=Số ca dương tính:Số ca xét nghiệm.

Bước 2: So sánh với 0,1.

Lời giải chi tiết :

Bước 1:

Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý I là $\dfrac{{21}}{{210}} = 0,1$

Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý II là $\dfrac{{15}}{{150}} = 0,1$

Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý III là $\dfrac{9}{{180}} = 0,05$

Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” của quý IV là $\dfrac{{48}}{{240}} = 0,2$

Bước 2:

Ta có một số nhỏ hơn 0,1 là 0,05.

Vậy có 1 quý có xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính” dưới 0,1.

Câu 19

Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là

A.

0,1
B.

0,25
C.

0,15
D.

0,125

Đáp án: A

Phương pháp giải :

- Xác định số ca dương tính quý I.

- Xác suất thực nghiệm=Số ca dương tính:Số ca xét nghiệm.

Lời giải chi tiết :

Số ca xét nghiệm quý I là 210.

Số ca dương tính là 21 ca.

Xác suất thực nghiệm của sự kiện “một ca có kết quả dương tính quý I” là

$\dfrac{{21}}{{210}} = 0,1$

Câu 20 :

Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?

A.

$\dfrac{7}{{11}}$
B.

$\dfrac{4}{{11}}$
C.

$\dfrac{4}{7}$
D.

$\dfrac{3}{7}$

Đáp án : A

Phương pháp giải :

- Xác định tổng số lần gieo và số lần gieo được mặt N.

- Xác suất thực nghiệm= Số lần được mặt N: Tổng số lần gieo

Lời giải chi tiết :

Tổng số lần gieo là 22.

Số lần gieo được mặt N là 14.

Xác suất thực nghiệm xuất hiện mặt N là: $\dfrac{{14}}{{22}} = \dfrac{7}{{11}}$

Trắc nghiệm Bài 2: Xác suất thực nghiệm Toán 6 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 2: Xác suất thực nghiệm Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 1: Phép thử nghiệm – Sự kiện Toán 6 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 1: Phép thử nghiệm – Sự kiện Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Bài giải mới nhất

Trắc nghiệm Bài tập ôn tập chương 9: Một số yếu tố thống kê Toán 6 Chân trời sáng tạo

Báo lỗi góp ý