-
Chương 1: Số tự nhiên
- Bài 1: Tập hợp. Phần tử của tập hợp
- Các dạng toán về tập hợp, phần tử của tập hợp
- Bài 2: Tập hợp số tự nhiên. Ghi số tự nhiên
- Các dạng toán về tập hợp số tự nhiên, ghi số tự nhiên
- Bài 3. Phép cộng và phép nhân
- Các dạng toán về phép cộng và phép nhân
- Các dạng toán về phép cộng và phép nhân (tiếp)
- Bài 3: Phép trừ và phép chia
- Các dạng toán về phép trừ và phép chia
- Bài 4: Lũy thừa với số mũ tự nhiên
- Các dạng toán về lũy thừa với số mũ tự nhiên
- Bài 5: Thứ tự thực hiện các phép tính
- Các dạng toán về thứ tự thực hiện các phép tính
- Bài 6: Chia hết và chia có dư. Tính chất chia hết của một tổng
- Các dạng toán về chia hết và chia có dư, tính chất chia hết của một tổng
- Bài 7: Dấu hiệu chia hết cho 2, cho 5
- Các dạng toán về dấu hiệu chia hết cho 2, cho 5
- Bài 8: Dấu hiệu chia hết cho 3, cho 9
- Các dạng toán về dấu hiệu chia hết cho 3, cho 9
- Bài 9: Ước và bội
- Các dạng toán về ước và bội
- Bài 10: Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố
- Các dạng toán về số nguyên tố, hợp số, phân tích một số ra thừa số nguyên tố
- Bài 12: Ước chung. Ước chung lớn nhất
- Các dạng toán về ước chung, ước chung lớn nhất
- Bài 13: Bội chung. Bội chung nhỏ nhất
- Các dạng toán về bội chung, bội chung nhỏ nhất
- Bài tập ôn tập chương 1: Số tự nhiên
-
Chương 2. Số nguyên
- Bài 1: Số nguyên âm và tập hợp các số nguyên
- Các dạng toán về số nguyên âm và tập hợp các số nguyên
- Bài 2: Thứ tự trong tập hợp số nguyên
- Các dạng toán về thứ tự trong tập hợp số nguyên
- Bai 3: Phép cộng hai số nguyên và tính chất phép cộng hai số nguyên
- Bài 3 (tiếp) Phép trừ hai số nguyên và quy tắc dấu ngoặc
- Các dạng toán về phép cộng và phép trừ hai số nguyên
- Các dạng toán về phép cộng trừ hai số nguyên (tiếp)
- Bài 4: Phép nhân hai số nguyên
- Bài 4 (tiếp) Phép chia hết, bội và ước của một số nguyên
- Các dạng toán về phép nhân và phép chia hai số nguyên
- Các dạng toán về phép nhân và phép chia hết hai số nguyên (tiếp)
- Bài tập ôn tập chương 2: Số nguyên
-
Chương 3. Hình học trực quan. Các hình phẳng trong thực tiễn
-
Chương 4. Một số yếu tố thống kê
-
Chương 5. Phân số
- Bài 1: Phân số với tử số và mẫu số là số nguyên
- Các dạng toán về phân số với tử số và mẫu số là số nguyên
- Bài 2: Tính chất cơ bản của phân số
- Các dạng toán về tính chất cơ bản của phân số
- Bài 3: So sánh phân số
- Bài 4: Phép cộng và phép trừ phân số
- Các dạng toán về phép cộng và phép trừ phân số
- Bài 5: Phép nhân và phép chia phân số
- Các dạng toán về phép nhân và phép chia phân số
- Bài 6: Giá trị phân số của một số
- Bài 7: Hỗn số
- Bài tập ôn tập chương 5: Phân số
-
Chương 6. Số thập phân
-
Chương 7. Hình học trực quan. Tính đối xứng của hình phẳng trong thế giới tự nhiên
-
Chương 8. Hình học phẳng. Các hình hình học cơ bản
- Bài 1: Điểm. Đường thẳng
- Bài 2: Ba điểm thẳng hàng. Ba điểm không thẳng hàng
- Bài 3: Hai đường thẳng cắt nhau, song song. Tia
- Bài 4: Đoạn thẳng. Độ dài đoạn thẳng
- Bài 5: Trung điểm của đoạn thẳng
- Bài 6: Góc
- Bài 7: Số đo góc. Các góc đặc biệt
- Bài tập ôn tập chương 8: Hình học phẳng. Các hình hình học cơ bản
-
Chương 9. Một số yếu tố xác suất
Trắc nghiệm Bài 3: Phép trừ và phép chia Toán 6 Chân trời sáng tạo
Đề bài
Phép tính \(x - 5\) thực hiện được khi
-
A.
\(x < 5\)
-
B.
\(x \ge 5\)
-
C.
\(x < 4\)
-
D.
\(x = 3\)
Cho phép tính \(231 - 87\). Chọn câu đúng.
-
A.
\(231\) là số trừ
-
B.
\(87\) là số bị trừ
-
C.
\(231\) là số bị trừ
-
D.
\(87\) là hiệu
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
-
A.
\(x\)
-
B.
\(6\)
-
C.
\(3\)
-
D.
\(18\)
Tính 1 454-997
-
A.
575
-
B.
567
-
C.
457
-
D.
754
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho:
\(a = b.q + r\)
Khẳng định nào sau đây đúng?
-
A.
\(r \ge b\)
-
B.
\(0 < b < r\)
-
C.
\(0 < r < b\)
-
D.
\(0 \le r < b\)
Biểu diễn phép chia \(445:13\) dưới dạng \(a = b.q + r\) trong đó \(0 \le r < b\)
-
A.
\(445 = 13.34 + 3\)
-
B.
\(445 = 13.3 + 34\)
-
C.
\(445 = 34.3 + 13\)
-
D.
\(445 = 13.34\)
-
A.
1
-
B.
2
-
C.
3
-
D.
4
-
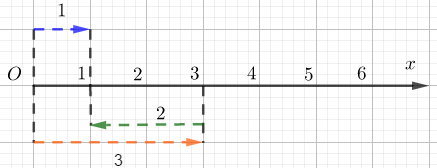
A.
Phép cộng của 1 và 2
-
B.
Phép trừ của 3 và 2
-
C.
Phép cộng của 1 và 3
-
D.
Phép trừ của 3 và 1
Dạng tổng quát của số tự nhiên chia hết cho \(3\) là:
-
A.
\(3k\,\left( {k \in N} \right)\)
-
B.
\(5k + 3\,\left( {k \in N} \right)\)
-
C.
\(3k + 1\,\left( {k \in N} \right)\)
-
D.
\(3k + 2\,\left( {k \in N} \right)\)
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là
-
A.
\(2k + 5\,\left( {k \in N} \right)\)
-
B.
\(5k + 2\,\left( {k \in N} \right)\)
-
C.
\(2k\,\left( {k \in N} \right)\)
-
D.
\(5k + 4\,\left( {k \in N} \right)\)
Tình nhanh \(49.15 - 49.5\) ta được kết quả là
-
A.
\(490\)
-
B.
\(49\)
-
C.
\(59\)
-
D.
\(4900\)
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Lời giải và đáp án
Phép tính \(x - 5\) thực hiện được khi
-
A.
\(x < 5\)
-
B.
\(x \ge 5\)
-
C.
\(x < 4\)
-
D.
\(x = 3\)
Đáp án : B
Phép tính \(a - b\) thực hiện được khi \(a \ge b.\)
Phép tính \(x - 5\) thực hiện được khi \(x \ge 5.\)
Cho phép tính \(231 - 87\). Chọn câu đúng.
-
A.
\(231\) là số trừ
-
B.
\(87\) là số bị trừ
-
C.
\(231\) là số bị trừ
-
D.
\(87\) là hiệu
Đáp án : C
Trong phép trừ $a - b = x$ thì \(a\) là số bị trừ; \(b\) là số trừ và \(x\) là hiệu.
Trong phép trừ \(231 - 87\) thì \(231\) là số bị trừ và \(87\) là số trừ nên C đúng.
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
-
A.
\(x\)
-
B.
\(6\)
-
C.
\(3\)
-
D.
\(18\)
Đáp án : B
Ta sử dụng (số bị chia) : (số chia) = (thương) để xác định thương của phép chia
Phép chia \(x:3 = 6\) có \(x\) là số bị chia; \(3\) là số chia và \(6\) là thương.
Nên thương của phép chia là \(6.\)
Tính 1 454-997
-
A.
575
-
B.
567
-
C.
457
-
D.
754
Đáp án : C
- Thêm vào số bị trừ và số trừ cùng một số sao cho số trừ mới là số tròn chục, tròn trăm, tròn nghìn.
- Tính: (số bị trừ mới) – (số trừ mới).
1 454-997 = (1 454+3)-(997+3)
= 1 457-1 000=457
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho:
\(a = b.q + r\)
Khẳng định nào sau đây đúng?
-
A.
\(r \ge b\)
-
B.
\(0 < b < r\)
-
C.
\(0 < r < b\)
-
D.
\(0 \le r < b\)
Đáp án : C
Định nghĩa về phép chia hết và phép chia có dư.
Khi chia a cho b, trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho:
\(a = b.q + r\) trong đó \(0 \le r < b\)
Phép chia a cho b là phép chia có dư nên \(r \ne 0\)
Vậy \(0 < r < b\).
Biểu diễn phép chia \(445:13\) dưới dạng \(a = b.q + r\) trong đó \(0 \le r < b\)
-
A.
\(445 = 13.34 + 3\)
-
B.
\(445 = 13.3 + 34\)
-
C.
\(445 = 34.3 + 13\)
-
D.
\(445 = 13.34\)
Đáp án : A
Đặt tính rồi tính.
Xác định a,b,q,r trong phép chia vừa nhận được.
Số bị chia là \(b = 445\), số chia là \(b = 13\) thương \(q = 34\), số dư là \(r = 3\). Ta biểu diễn phép chia như sau: \(445 = 13.34 + 3\)
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : C
Đặt tính rồi tính.
Đếm số các phép chia có dư.
Vậy có 3 phép chia có dư
-
A.
Phép cộng của 1 và 2
-
B.
Phép trừ của 3 và 2
-
C.
Phép cộng của 1 và 3
-
D.
Phép trừ của 3 và 1
Đáp án : B
Số 3 và số 1 cùng chiều từ trái sang phải, số 2 ngược chiều với hai số này. Mà ta có 3-2=1 nên hình ảnh trên minh họa cho phép trừ 3-2.
Dạng tổng quát của số tự nhiên chia hết cho \(3\) là:
-
A.
\(3k\,\left( {k \in N} \right)\)
-
B.
\(5k + 3\,\left( {k \in N} \right)\)
-
C.
\(3k + 1\,\left( {k \in N} \right)\)
-
D.
\(3k + 2\,\left( {k \in N} \right)\)
Đáp án : A
Sử dụng các số hạng chia hết cho \(a\) có dạng $x = a.k\,\left( {k \in N} \right)$
Các số hạng chia hết cho \(3\) có dạng tổng quát là \(x = 3k\,\left( {k \in N} \right)\)
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là
-
A.
\(2k + 5\,\left( {k \in N} \right)\)
-
B.
\(5k + 2\,\left( {k \in N} \right)\)
-
C.
\(2k\,\left( {k \in N} \right)\)
-
D.
\(5k + 4\,\left( {k \in N} \right)\)
Đáp án : B
Số tự nhiên \(a\) chia cho \(b\) được thương \(q\) và dư $r$ có dạng \(a = b.q + r.\)
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là \(a = 5k + 2\,\left( {k \in N} \right).\)
Tình nhanh \(49.15 - 49.5\) ta được kết quả là
-
A.
\(490\)
-
B.
\(49\)
-
C.
\(59\)
-
D.
\(4900\)
Đáp án : A
Sử dụng tính chất phân phối của phép nhân với phép trừ \(ab - ac = a\left( {b - c} \right).\)
Ta có \(49.15 - 49.5\)\( = 49.\left( {15 - 5} \right) = 49.10 = 490.\)
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Đáp án : D
Sử dụng tính chất phân phối của phép nhân với phép cộng; phép trừ \(ab + ac - ad = a\left( {b + d - c} \right).\)
Ta có $12.100 + 100.36 - 100.19$\( = 100.\left( {12 + 36 - 19} \right) = 100.29 = 2900.\)
Luyện tập và củng cố kiến thức Các dạng toán về phép trừ và phép chia Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Lũy thừa với số mũ tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về lũy thừa với số mũ tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Thứ tự thực hiện các phép tính Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về thứ tự thực hiện các phép tính Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 6: Chia hết và chia có dư. Tính chất chia hết của một tổng Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về chia hết và chia có dư, tính chất chia hết của một tổng Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 7: Dấu hiệu chia hết cho 2, cho 5 Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về dấu hiệu chia hết cho 2, cho 5 Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 8: Dấu hiệu chia hết cho 3, cho 9 Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về dấu hiệu chia hết cho 3, cho 9 Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 9: Ước và bội Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về ước và bội Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 10: Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về số nguyên tố, hợp số, phân tích một số ra thừa số nguyên tố Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 12: Ước chung. Ước chung lớn nhất Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về ước chung, ước chung lớn nhất Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 13: Bội chung. Bội chung nhỏ nhất Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về bội chung, bội chung nhỏ nhất Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 1: Số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép cộng và phép nhân (tiếp) Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép cộng và phép nhân Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3. Phép cộng và phép nhân Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về tập hợp số tự nhiên, ghi số tự nhiên Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Tập hợp số tự nhiên. Ghi số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về tập hợp, phần tử của tập hợp Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Tập hợp. Phần tử của tập hợp Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài tập ôn tập chương 9: Một số yếu tố thống kê Toán 6 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Xác suất thực nghiệm Toán 6 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Phép thử nghiệm – Sự kiện Toán 6 Chân trời sáng tạo
- Trắc nghiệm Bài tập ôn tập chương 8: Hình học phẳng. Các hình hình học cơ bản Toán 6 Chân trời sáng tạo
- Trắc nghiệm Bài 7: Số đo góc. Các góc đặc biệt Toán 6 Chân trời sáng tạo
