 Toán 7, giải toán lớp 7 kết nối tri thức với cuộc sống
Toán 7, giải toán lớp 7 kết nối tri thức với cuộc sống
 Bài 9. Hai đường thẳng song song và dấu hiệu nhận biết ..
Bài 9. Hai đường thẳng song song và dấu hiệu nhận biết ..
Giải mục 1 trang 46, 47 SGK Toán 7 tập 1 - Kết nối tri thức
Cho đường thẳng mn cắt đường thẳng xy và uv lần lượt tại hai điểm P và Q (H.3.17).Em hãy kể tên:.. Trên Hình 3.18, cho biết hai góc so le trong
Câu hỏi 1
Cho đường thẳng mn cắt đường thẳng xy và uv lần lượt tại hai điểm P và Q (H.3.17).Em hãy kể tên:
a) Hai cặp góc so le trong
b) Bốn cặp góc đồng vị.
Phương pháp giải:
Vẽ hình, nhận diện các cặp góc so le trong, đồng vị.
Lời giải chi tiết:
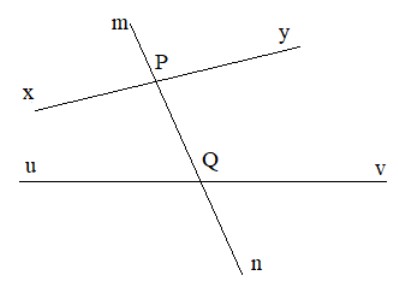
a) Hai cặp góc so le trong là: góc xPn và góc mQv; góc yPn và góc uQm
b) Bốn cặp góc đồng vị là: góc mPy và góc mQv; góc yPn và góc vQn; góc mPx và góc mQu; góc xPn và góc uQn.
HĐ 1
Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng \(60^\circ \).
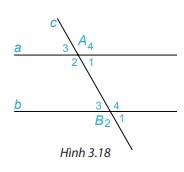
Hãy tính và so sánh hai góc so le trong còn lại A2 và B4.
Phương pháp giải:
Sử dụng tính chất 2 góc kề bù: Tổng 2 góc kề bù bằng 180 độ
Lời giải chi tiết:
+) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l}60^\circ + \widehat {{A_2}} = 180^\circ \\ \text{suy ra } \widehat {{A_2}} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
+) Vì \(\widehat {{B_3}} + \widehat {{B_4}} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l}60^\circ + \widehat {{B_4}} = 180^\circ \\ \text{suy ra } \widehat {{B_4}} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Vậy hai góc so le trong còn lại A2 và B4 bằng nhau và bằng \(120^\circ \).
HĐ 2
Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng \(60^\circ \).
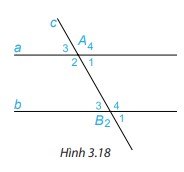
Chọn hai góc đồng vị rồi tính và so sánh hai góc đó.
Phương pháp giải:
Sử dụng tính chất: Tổng 2 góc kề bù bằng 180 độ hoặc 2 góc đối đỉnh thì bằng nhau
Lời giải chi tiết:
Chọn cặp góc đồng vị: góc A1 và góc B1
Ta có: \(\widehat {{A_1}} = 60^\circ ;\widehat {{B_3}} = 60^\circ \)
\(\widehat {{B_1}} = \widehat {{B_3}}\) (2 góc đối đỉnh)
suy ra \(\widehat {{B_1}} = 60^\circ \)
Vậy hai góc A1 và góc B1 đồng vị bằng nhau và bằng \(60^0\)
Luyện tập 1
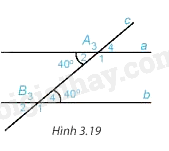
Quan sát Hình 3.19.
a) Biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).
Phương pháp giải:
Sử dụng tính chất: Tổng 2 góc kề bù bằng 180 độ hoặc 2 góc đối đỉnh thì bằng nhau
Đường thẳng c cắt 2 đường thẳng, tạo thành 1 cặp góc so le trong bằng nhau.
Lời giải chi tiết:
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\(\widehat {{A_1}} + 40^\circ = 180^\circ \)
suy ra \(\widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{A_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong nên a // b
Suy ra 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)
- Giải mục 2 trang 47, 48, 49 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 3.6 trang 49 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 3.7 trang 49 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 3.8 trang 49 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 3.9 trang 49 SGK Toán 7 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết quan hệ giữa ba cạnh của một tam giác Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác Toán 7 Kết nối tri thức
- Giải câu hỏi trang 108, 109 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Giải mục 2 trang 104 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Lý thuyết quan hệ giữa ba cạnh của một tam giác Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác Toán 7 Kết nối tri thức
- Giải câu hỏi trang 108, 109 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Giải mục 2 trang 104 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2












Danh sách bình luận