Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức

Khái niệm về đường vuông góc, đường xiên và hình chiếu của đường xiên

1. Khái niệm về đường vuông góc, đường xiên và hình chiếu của đường xiên

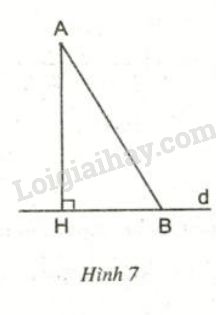
Từ \(A\) không nằm trên \(d\), kẻ một đường thẳng vuông góc với \(d\) tại \(H\). Trên \(d\) lấy điểm \(B\) không trùng với \(H\). Khi đó:

+ Đoạn \(AH\) gọi là đoạn vuông góc hay đường vuông góc kẻ từ \(A\) đến \(d\).

+ Đoạn \(AB\) gọi là đường xiên kẻ từ \(A\) đến \(d\)

+ Đoạn \(HB\) gọi là hình chiếu của đường xiên \(AB\) lên đường thẳng \(d\).

2. Quan hệ giữa đường vuông góc và đường xiên

Định lý 1: Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.

3. Quan hệ giữa các đường xiên và hình chiếu của chúng

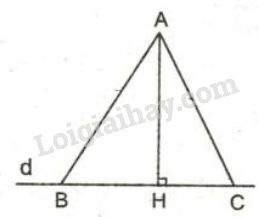
Định lý 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó;

a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn

b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn

c) Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.

4. Các dạng toán thường gặp

Dạng 1: Chỉ ra hai đường xiên bằng nhau hoặc hai hình chiếu bằng nhau

Phương pháp:

Ta sử dụng: “Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.”

Dạng 2: So sánh hai đường xiên hoặc hai hình chiếu

Phương pháp:

Ta sử dụng định lý:

Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:

+ Đường xiên nào có hình chiếu lớn hơn thì lớn hơn

+ Đường xiên nào lớn hơn thì có hình chiếu lớn hơn

+ Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.

Dạng 3: Quan hệ giữa đường vuông góc và đường xiên

Phương pháp:

Ta sử dụng định lý:

Trong các đường vuông góc và đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, đường vuông góc ngắn hơn mọi đường xiên.

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 11 phiếu

Bài tiếp theo

Giải bài 9.9 trang 65 SGK Toán 7 tập 2 - Kết nối tri thức
Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC ( M,N không phải là đỉnh của tam giác) (H. 9.13) . Chứng minh rằng MN < BC.
Giải bài 9.8 trang 65 SGK Toán 7 tập 2 - Kết nối tri thức
Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C. ( H. 9.12) a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất. b) Chứng minh rằng với mọi điểm M thì AM < AB
Giải bài 9.7 trang 65 SGK Toán 7 tập 2 - Kết nối tri thức
Cho hình vuông ABCD. Hỏi trong bốn đỉnh của hình vuông a) Đỉnh nào cách đều hai điểm A và C? b) Đỉnh nào cách đều hai đường thẳng AB và AD?
Giải bài 9.6 trang 65 SGK Toán 7 tập 2 - Kết nối tri thức
Chiều cao của tam giác ứng với một cạnh của nó có phải là khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó không?
Giải câu hỏi trang 63,64 SGK Toán 7 tập 2 - Kết nối tri thức
Cho điểm A không nằm trên đường thẳng d. a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d. b) Em hãy giải thích vì sao AH < AM
Lý thuyết quan hệ giữa đường vuông góc và đường xiên Toán 7 Kết nối tri thức
Khái niệm về đường vuông góc và đường xiên