-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Bài 5: Khoảng cách
Câu 35 trang 118 SGK Hình học 11 Nâng cao
Cho tứ diện ABCD. Chứng minh rằng nếu AC = BD, AD = BC thì đường vuông góc chung của AB và CD là đường thẳng nối trung điểm của AB và CD. Điều ngược lại có đúng không ?
Đề bài
Cho tứ diện ABCD. Chứng minh rằng nếu AC = BD, AD = BC thì đường vuông góc chung của AB và CD là đường thẳng nối trung điểm của AB và CD. Điều ngược lại có đúng không ?
Lời giải chi tiết
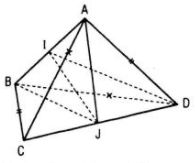
a. Vì AC = BD, AD = BC nên tam giác ACD bằng tam giác BDC, từ đó hai trung tuyến tương ứng AJ và BJ bằng nhau (ở đó J là trung điểm của CD). Gọi I là trung điểm của AB thì ta có JI ⊥ AB.
Tương tự như trên ta cũng có JI ⊥ CD. Vậy JI là đường vuông góc chung của AB và CD.
b. Điều ngược lại của kết luận nêu ra trong bài toán cũng đúng, tức là nếu IJ ⊥ AB, IJ ⊥ CD, I, J lần lượt là trung điểm của AB và CD thì AC = BD; AD = BC.
Thật vậy, vì IJ ⊥ AB, I là trung điểm của AB nên AJ = BJ. Mặt khác :
\(\eqalign{ & A{C^2} + A{D^2} = 2A{J^2} + {{C{D^2}} \over 2} \cr & B{C^2} + B{D^2} = 2B{J^2} + {{C{D^2}} \over 2} \cr} \)
Từ đó ta có : \(A{C^2} + A{D^2} = B{C^2} + B{D^2}\) (1)
Tương tự như trên ta cũng có :
\(C{B^2} + C{A^2} = D{B^2} + D{A^2}\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta suy ra \(A{D^2} - B{C^2} = B{C^2} - D{A^2},\) tức là DA = BC và từ (1) ta cũng có AC = BD.
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 34 trang 118 SGK Hình học 11 Nâng cao
- Câu 33 trang 118 SGK Hình học 11 Nâng cao
- Câu 32 trang 117 SGK Hình học 11 Nâng cao
- Câu 31 trang 117 SGK Hình học 11 Nâng cao
- Câu 30 trang 117 SGK Hình học 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
