Câu 3.33 trang 63 SBT Đại số 10 Nâng cao

Giải bài tập Câu 3.33 trang 63 SBT Đại số 10 Nâng cao

Đề bài

Cho tam giác ABC nhọn có cạnh BC = a, đường cao AH = h. Một hình chữ nhật MNPQ nội tiếp trong tam giác (M ∈ AB; N ∈ AC ; P, Q ∈ BC) có chu vi bằng 2p (p là độ dài cho trước). Hãy tính độ dài cạnh PQ của hình chữ nhật MNPQ, biện luận theo p, a, h.

Lời giải chi tiết

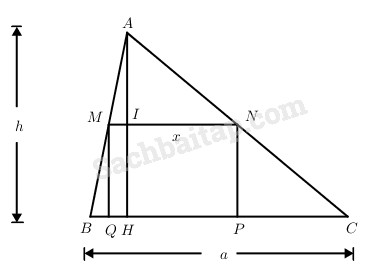
Đặt PQ = MN = x (0 < x < a)

Theo định lí Ta-lét ta có (h.3.1)

\(\begin{array}{l}\dfrac{{MN}}{{BC}} = \dfrac{{AI}}{{AH}}\left( { = \dfrac{{AN}}{{AC}}} \right)\\ \Rightarrow \dfrac{{\rm{x}}}{a} = \dfrac{{h - IH}}{h} \Rightarrow IH = \dfrac{{\left( {{\rm{a}} - x} \right)h}}{a}\end{array}\)

Điều kiện

\(MN + IH = p\) cho ta phương trình \(x + \dfrac{{\left( {{\rm{a}} - x} \right)h}}{a} = p\) hay\(\left( {{\rm{a}} - h} \right)x = a\left( {p - h} \right)\) (1)

- Nếu a = h thì phương trình (1) vô nghiệm khi p ≠ h, nghiệm đúng với mọi x khi p = h. Điều này có nghĩa là :

+ Khi tam giác nhọn ABC có AH = BC và p ≠ AH thì không có hình chữ nhật nào thỏa mãn điều kiện của bài toán.

+ Khi tam giác nhọn ABC có AH = BC và p = AH thì có vô số hình chữ nhật thỏa mãn điều kiện bài toán với cạnh x (0 < x < a tùy ý).

- Nếu a ≠ h thì phương trình (1) có nghiệm duy nhất \(x = \dfrac{{a\left( {p - h} \right)}}{{a - h}}.\) (2)

Xét điều kiện 0 < x < a hay

\(0 < \dfrac{{a\left( {p - h} \right)}}{{a - h}} < a\)

Vì a ≠ h nên có hai trường hợp :

+ Nếu a > h, ta có

\((2) ⇔ 0 < p – h < a – h ⇔ h < p < a\)

+ Nếu a < h, ta có

\((2) ⇔ 0 > p – h > a – h ⇔ a < p < h.\)

Điều này có nghĩa là, giá trị \(x = \dfrac{{a\left( {p - h} \right)}}{{a - h}}\) là nghiệm của bài toán khi và chỉ khi p nằm giữa a và h.