 Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
 Bài 4. Biến cố và xác suất của biến cố
Bài 4. Biến cố và xác suất của biến cố
Câu 28 trang 76 SGK Đại số và Giải tích 11 Nâng cao
Gieo hai con súc sắc cân đối.
Gieo hai con súc sắc cân đối.
LG a
Mô tả không gian mẫu.
Phương pháp giải:
- Liệt kê các phần tử của không gian mẫu.
- Liệt kê các khả năng thuận lời cho từng biến cố A, B, C.
- Tính xác suất theo công thức \(P\left( A \right) = \dfrac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}}\)
Lời giải chi tiết:
Không gian mẫu có 36 phần tử.
LG b
Gọi A là biến cố “Tổng số chấm trên mặt xuất hiện của hai con súc sắc nhỏ hơn hoặc bằng 7”. Liệt kê các kết quả thuận lợi cho A. Tính P(A).
Phương pháp giải:
- Liệt kê các phần tử của không gian mẫu.
- Liệt kê các khả năng thuận lời cho từng biến cố A, B, C.
- Tính xác suất theo công thức \(P\left( A \right) = \dfrac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}}\)
Lời giải chi tiết:
Ta có:
\({\Omega _A} = \left\{ \begin{array}{l}
\left( {1;1} \right),\left( {1;2} \right),\left( {1;3} \right),\left( {1;4} \right),\left( {1;5} \right),\left( {1;6} \right)\\
\left( {2;1} \right),\left( {2;2} \right),\left( {2;3} \right),\left( {2;4} \right),\left( {2;5} \right),\\
\left( {3;1} \right),\left( {3;2} \right),\left( {3;3} \right),\left( {3;4} \right),\left( {4;1} \right),\\
\left( {4;2} \right),\left( {4;3} \right),\left( {5;1} \right),\left( {5;2} \right),\left( {6;1} \right)
\end{array} \right\}\)
Tập \({\Omega _A}\) có \(21\) phần tử.
Vậy \(\displaystyle P\left( A\right) = {{21} \over {36}}= {{7} \over {12}}\).
LG c
Cũng hỏi như trên cho các biến cố B : “Có ít nhất một con súc sắc xuất hiện mặt 6 chấm” và C “Có đúng một con súc sắc xuất hiện mặt 6 chấm”.
Phương pháp giải:
- Liệt kê các phần tử của không gian mẫu.
- Liệt kê các khả năng thuận lời cho từng biến cố A, B, C.
- Tính xác suất theo công thức \(P\left( A \right) = \dfrac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}}\)
Lời giải chi tiết:
\({\Omega _B} = \left\{ \begin{array}{l}\left( {6;1} \right),\left( {6;2} \right),\left( {6;3} \right),\left( {6;4} \right),\\\left( {6;5} \right),\left( {6;6} \right),\left( {1;6} \right),\left( {2;6} \right),\\\left( {3;6} \right),\left( {4;6} \right),\left( {5;6} \right)\end{array} \right\}\)
Tập \({\Omega _B}\) có \(11\) phần tử.
Vậy \(\displaystyle P\left( B\right) = {{11} \over {36}}\).
\({\Omega _C} = \left\{ \begin{array}{l}\left( {6;1} \right),\left( {6;2} \right),\left( {6;3} \right),\left( {6;4} \right),\left( {6;5} \right),\\\left( {1;6} \right),\left( {2;6} \right),\left( {3;6} \right),\left( {4;6} \right),\left( {5;6} \right)\end{array} \right\}\)
Vậy \({\Omega _C}\) có \(10\) phần tử.
Do đó \(\displaystyle P\left( C \right) = {{10} \over {36}} = {5 \over {18}}.\)
Loigiaihay.com




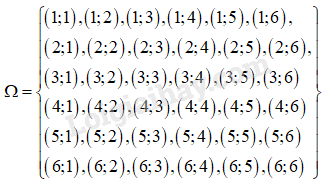








Danh sách bình luận