-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Bài 3: Đường thẳng vuông góc với mặt phẳng
Câu 17 trang 103 SGK Hình học 11 Nâng cao
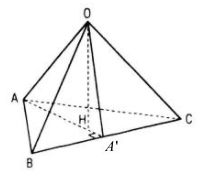
Cho hình tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc.
Cho hình tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc.
LG a
Chứng minh tam giác ABC có ba góc nhọn.
Lời giải chi tiết:
Đặt a = OA, b = OB, c = OC. Ta có:
\(AB = \sqrt {{a^2} + {b^2}} ,BC = \sqrt {{b^2} + {c^2}} ,\) \(AC = \sqrt {{a^2} + {c^2}} \)
Áp dụng định lí cosin trong tam giác ABC ta có :
\(\cos A = {{A{B^2} + A{C^2} - B{C^2}} \over {2AB.AC}} \) \( = {{{a^2} + {b^2} + {a^2} + {c^2} - {b^2} - {c^2}} \over {2AB.AC}} = {{2{a^2}} \over {2AB.AC}} > 0\)
⇒ A nhọn. Tương tự B, C là các góc nhọn.
Vậy ΔABC có ba góc nhọn.
LG b
Chứng minh rằng hình chiếu H của điểm O trên mp(ABC) trùng với trực tâm tam giác ABC.
Lời giải chi tiết:
LG c
Chứng minh rằng \({1 \over {O{H^2}}} = {1 \over {O{A^2}}} + {1 \over {O{B^2}}} + {1 \over {O{C^2}}}\)
Lời giải chi tiết:
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 18 trang 103 SGK Hình học 11 Nâng cao
- Câu 19 trang 103 SGK Hình học 11 Nâng cao
- Câu 20 trang 103 SGK Hình học 11 Nâng cao
- Câu 16 trang 103 SGK Hình học 11 Nâng cao
- Câu 15 trang 102 SGK Hình học 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
