Toán 11 Nâng cao

Bài 3: Đường thẳng vuông góc với mặt phẳng

Câu 15 trang 102 SGK Hình học 11 Nâng cao

Cho tứ diện ABCD. Tìm điểm O cách đều bốn đỉnh của tứ diện.

Đề bài

Cho tứ diện ABCD. Tìm điểm O cách đều bốn đỉnh của tứ diện.

Lời giải chi tiết

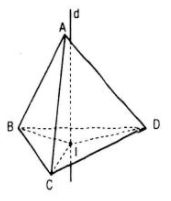
Gọi I là tâm đường tròn ngoại tiếp của ΔBCD

Gọi d là đường thẳng đi qua I và vuông góc với mặt phẳng (BCD)

Theo kết quả bài 14. M ϵ d ⇔ MB = MC = MD

(d gọi là trục của đường tròn ngoại tiếp tam giác BCD)

Gọi O là giao điểm của d với mặt phẳng trung trực của AB.

=> OA = OB ( vì O thuộc mặt phẳng trung trực của AB).

Và OB = OC = OD ( vì O thuộc đường thẳng d).

Suy ra :OA = OB = OC = OD hay O cách đều bốn đỉnh của tứ diện (O gọi là tâm mặt cầu ngoại tiếp tứ diện ABCD).

Loigiaihay.com

Bình luận

Bình chọn:

4.1 trên 7 phiếu

Các bài liên quan: - Bài 3: Đường thẳng vuông góc với mặt phẳng

Báo lỗi - Góp ý

>>Học trực tuyến Lớp 11 trên Tuyensinh247.com, mọi lúc, mọi nơi tất cả các môn. Các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu

Các bài khác cùng chuyên mục