-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Bài 1. Các hàm số lượng giác
Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao
a. Từ đồ thị của hàm số y = cosx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó :
a. Từ đồ thị của hàm số \(y = \cos x\), hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó:
\(y = \cos x + 2\)
\(y = \cos \left( {x - {\pi \over 4}} \right)\)
b. Hỏi mỗi hàm số đó có phải là hàm số tuần hoàn không ?
LG a
Từ đồ thị của hàm số \(y = \cos x\), hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó:
\(y = \cos x + 2\)
\(y = \cos \left( {x - {\pi \over 4}} \right)\)
Phương pháp giải:
Sử dụng lý thuyết tịnh tiến đồ thị:
Cho hàm số y=f(x) có đồ thị (C). Khi đó,
+) Hàm số y=f(x)+p có được do tịnh tiến (C) lên trên p đơn vị (p > 0)
+) Hàm số y=f(x-q) có được do tịnh tiến (C) sang phải q đơn vị (q > 0)
Lời giải chi tiết:
Đồ thị của hàm số \(y = \cos x + 2\) có được do tịnh tiến đồ thị của hàm số \(y = \cos x\) lên trên một đoạn có độ dài bằng \(2\)
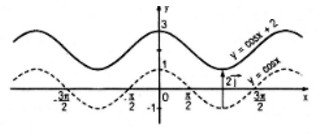
Đồ thị của hàm số \(y = \cos \left( {x - {\pi \over 4}} \right)\) có được do tịnh tiến đồ thị của hàm số y = cosx sang phải một đoạn có độ dài \({\pi \over 4}\)
Quảng cáo
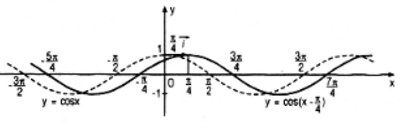
LG b
Hỏi mỗi hàm số đó có phải là hàm số tuần hoàn không ?
Lời giải chi tiết:
Các hàm số trên đều là hàm tuần hoàn vì:
nếu \(f(x) = \cos x + 2\) thì \(f(x + 2π) = \cos(x + 2π) + 2\)
\(= \cos x + 2 = f(x), ∀x \in\mathbb R\)
Và nếu \(g(x) = \cos \left( {x - {\pi \over 4}} \right)\) thì:
\(g(x + 2π) = \cos \left( {x + 2\pi - {\pi \over 4}} \right)\)
\(=\cos \left( {x - {\pi \over 4}} \right) = g\left( x \right)\) , \(∀x \in\mathbb R\)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 13 trang 17 SGK Đại số và Giải tích 11 Nâng cao
- Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao
- Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao
- Câu 9 trang 17 SGK Đại số và Giải tích 11 Nâng cao
- Câu 8 trang 16 SGK Đại số và Giải tích 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
