Bài 80 trang 155 SGK Đại số 10 nâng cao

Với giá trị nào của m, bất phương trình:

Đề bài

Với giá trị nào của m, bất phương trình:

(m²+ 1)x + m(x + 3) + 1 > 0

nghiệm đúng ∀x ∈ [-1; 2] ?

Phương pháp giải - Xem chi tiết

Tìm tập nghiệm S của bpt đã cho.

BPT nghiệm đúng với mọi x thuộc [-1;2] nếu \(\left[ { - 1;2} \right] \subset S\).

Lời giải chi tiết

Ta có:

\(\begin{array}{l}\left( {{m^2} + 1} \right)x + m\left( {x + 3} \right) + 1 > 0\\ \Leftrightarrow \left( {{m^2} + 1} \right)x + mx + 3m + 1 > 0\\ \Leftrightarrow \left( {{m^2} + m + 1} \right)x > - 3m - 1\\ \Leftrightarrow x > \frac{{ - 3m - 1}}{{{m^2} + m + 1}}\end{array}\)

(Vì \({m^2} + m + 1 \) \(= {\left( {m + \frac{1}{2}} \right)^2} + \frac{3}{4} > 0,\forall m\))

Tập nghiệm của bpt là \(S = \left( {\frac{{ - 3m - 1}}{{{m^2} + m + 1}}; + \infty } \right)\)

Để bpt nghiệm đúng với mọi \(x \in \left[ { - 1;2} \right]\) thì

\(\begin{array}{l}\left[ { - 1;2} \right] \subset S\\ \Leftrightarrow \frac{{ - 3m - 1}}{{{m^2} + m + 1}} < - 1\\ \Leftrightarrow - 3m - 1 < - {m^2} - m - 1\\\left( {Do\,{m^2} + m + 1 > 0} \right)\\ \Leftrightarrow {m^2} - 2m < 0\\ \Leftrightarrow 0 < m < 2\end{array}\)

Cách khác:

Ta có: (m² +1)x + m.(x+3)+ 1> 0

⇔ (m² + 1) x +mx + 3m +1 >0

⇔ (m² +1+ m). x+ 3m + 1 > 0

Đặt y = f(x) = (m² + m + 1)x+ 3m + 1

Ta coi y =f(x) là hàm số ẩn x và tham số m.

Đồ thị của hàm số y = f(x) là đường thẳng (Dm ).

Gọi Am và Bm là các điểm trên đường thẳng (Dm) có hoành độ theo thứ tự là -1 và 2.

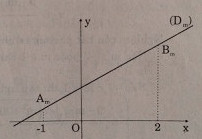
f(x) > 0 với ∀x ∈ [-1; 2] khi và chỉ khi đoạn thẳng A_mB_m nằm phía trên trục hoành. Điều này xảy ra khi và chỉ khi A_m và B_mnằm phía trên trục hoành, tức là:

\(\left\{ \matrix{
f( - 1) > 0 \hfill \cr
f(2) > 0 \hfill \cr} \right.\)

Mà \(f\left( { - 1} \right) = \left( {{m^2} + m + 1} \right).\left( { - 1} \right) + 3m + 1\)\( = - {m^2} + 2m\)

\(f\left( 2 \right) = \left( {{m^2} + m + 1} \right).2 + 3m + 1\)\( = 2{m^2} + 5m + 3\)

Nên \(\left\{ \begin{array}{l} - {m^2} + 2m > 0\\2{m^2} + 5m + 3 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}0 < m < 2\\\left[ \begin{array}{l}m > - 1\\m < - \frac{3}{2}\end{array} \right.\end{array} \right. \Leftrightarrow 0 < m < 2\)

Vậy \(0 < m < 2\).

Loigiaihay.com