Bài 47 trang 135 SGK Đại số 10 nâng cao

Gọi (S) là tập hợp các điểm trong mặt phẳng tọa độ có tọa độ thỏa mãn hệ:

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

Gọi (S) là tập hợp các điểm trong mặt phẳng tọa độ có tọa độ thỏa mãn hệ:

\(\left\{ \matrix{
2x - y \ge 2 \hfill \cr
x - 2y \le 2 \hfill \cr
x + y \le 5 \hfill \cr
x \ge 0 \hfill \cr} \right.\)

LG a

Hãy xác định (S) để thấy rằng đó là một tam giác.

Lời giải chi tiết:

Lần lượt dựng các đường thẳng:

\((d_1):-2x + y = -2;\) \((d_2): x – 2y = 2; \) \((d_3):x + y = 5\) và \((d_4):x = 0\).

Xét điểm M(1;1) ta thấy, M thuộc miền nghiệm của bpt 2, 3, 4 nhưng không thuộc miền nghiệm của 1.

Từ đó ta có miền nghiệm của hệ bất phương trình.

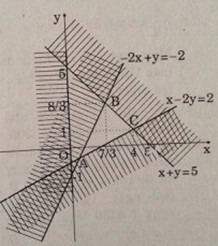
Tập nghiệm S được biểu diễn bằng miền trong của tam giác ABC với:

\(A({2 \over 3};\, - {2 \over 3});\,\,B({7 \over 3};\,{8 \over 3});\,C(4,\,1)\)

Ở đó, A là giao điểm của \((d_1)\) và \((d_2)\).

B là giao điểm của \((d_1)\) và \((d_3)\).

C là giao điểm của \((d_2)\) và \((d_3)\).

LG b

Trong (S) hãy tìm điểm có tọa độ \((x; y)\) làm cho biểu thức \(f(x;y)=y-x\) có giá trị nhỏ nhất, biết rằng \(f(x;y)\) có giá trị nhỏ nhất tại một trong các đỉnh của (S).

Lời giải chi tiết:

Tại \(A({2 \over 3};\, - {2 \over 3}) \Rightarrow F = - \frac{2}{3} - \frac{2}{3}= - {4 \over 3}\)

Tại \(B({7 \over 3};\,{8 \over 3}) \Rightarrow F =\frac{8}{3} - \frac{7}{3}= {1 \over 3}\)

Tại \(C(4; 1)\) thì \(F = 1-4=-3\)

Vậy F đạt giá trị nhỏ nhất bằng -3 tại \(C(4, 1)\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 13 phiếu

Bài tiếp theo

Bài 48 trang 135 SGK Đại số 10 nâng cao
Bài toán vitamin.
Bài 46 trang 135 SGK Đại số 10 nâng cao
Xác định miền nghiệm của các hệ bất phương trình hai ẩn
Bài 45 trang 135 SGK Đại số 10 nâng cao
Xác định miền nghiệm của các hệ bất phương trình hai ẩn
Bài 44 trang 132 SGK Đại số 10 nâng cao
Viết các phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi biểu diễn hình học miền nghiệm (S) của hệ đó.
Bài 43 trang 132 SGK Đại số 10 nâng cao
Xác định tập nghiệm của mỗi hệ bất phương trình hai ẩn
Bài 42 trang 132 SGK Đại số 10 nâng cao
Xác định miền nghiệm của mỗi bất phương trình hai ẩn