Bài 45 trang 135 SGK Đại số 10 nâng cao

Xác định miền nghiệm của các hệ bất phương trình hai ẩn

Lựa chọn câu để xem lời giải nhanh hơn

Xác định miền nghiệm của các hệ bất phương trình hai ẩn

LG a

\(x+ 3+ 2(2y + 5) < 2(1 – x)\)

Phương pháp giải:

- Vẽ đường thẳng (d): ax+by+c=0

- Xét một điểm \(M(x_0;y_0)\) không nằm trên (d).

Nếu tọa độ điểm M thỏa mãn bpt đang xét thì miền nghiệm là nửa mặt phẳng bờ (d) chứa M (biên phụ thuộc vào dấu bất đẳng thức).

Nếu tọa độ điểm M không thỏa mãn bpt đang xét thì miền nghiệm là nửa mặt phẳng bờ (d) không chứa M (biên phụ thuộc vào dấu bất đẳng thức).

Lời giải chi tiết:

Ta có:

\(x + 3+ 2(2y + 5) < 2(1 – x)\)\( \Leftrightarrow x + 3 + 4y + 10 < 2 - 2x\)

\(⇔ 3x + 4y + 11 < 0\)

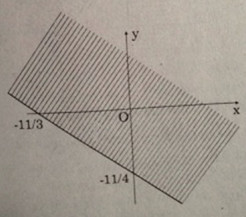
Vẽ đường thẳng (d): 3x + 4y + 11 = 0.

+) Cho x=0 thì y=-11/4 ta được điểm (0;-11/4).

+) Cho y=0 thì x=-11/3 ta được điểm (-11/3;0).

Đường thẳng (d) đi qua hai điểm trên.

Xét điểm O(0;0) ta có: 3.0 + 4.0 + 11 > 0 nên O không thuộc miền nghiệm.

Vậy miền nghiệm là phần mặt phẳng không bị gạch chéo, không kể bờ (d).

LG b

\((1 + \sqrt 3 )x - (1 - \sqrt 3 )y \ge 2\)

Lời giải chi tiết:

Ta có:

\(\eqalign{
& (1 + \sqrt 3 )x - (1 - \sqrt 3 )y \ge 2 \cr
& \Leftrightarrow (1 + \sqrt 3 )x - (1 - \sqrt 3 )y - 2 \ge 0 \cr} \)

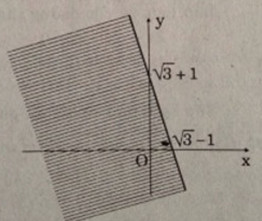
Vẽ đường thẳng (d): \((1 + \sqrt 3 )x - (1 - \sqrt 3 )y - 2 = 0\).

+) Cho x=0 thì \(y = - \frac{2}{{1 - \sqrt 3 }} = 1 + \sqrt 3 \) ta được điểm \(\left( {0;1 + \sqrt 3 } \right)\)

+) Cho y=0 thì \(x = \frac{2}{{1 + \sqrt 3 }} = - 1 + \sqrt 3 \) ta được điểm \((- 1 + \sqrt 3;0)\).

Đường thẳng (d) đi qua hai điểm trên.

Xét điểm O(0;0) có: \((1 + \sqrt 3 ).0 - (1 - \sqrt 3 ).0 - 2 = -2<0\) nên O không thuộc miền nghiệm.

Vậy miền nghiệm là phần mặt phẳng không bị gạch chéo kể cả bờ (d).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 38 phiếu

Bài 46 trang 135 SGK Đại số 10 nâng cao
Xác định miền nghiệm của các hệ bất phương trình hai ẩn
Bài 47 trang 135 SGK Đại số 10 nâng cao
Gọi (S) là tập hợp các điểm trong mặt phẳng tọa độ có tọa độ thỏa mãn hệ:
Bài 48 trang 135 SGK Đại số 10 nâng cao
Bài toán vitamin.
Bài 44 trang 132 SGK Đại số 10 nâng cao
Viết các phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi biểu diễn hình học miền nghiệm (S) của hệ đó.
Bài 43 trang 132 SGK Đại số 10 nâng cao
Xác định tập nghiệm của mỗi hệ bất phương trình hai ẩn
Bài 42 trang 132 SGK Đại số 10 nâng cao
Xác định miền nghiệm của mỗi bất phương trình hai ẩn