Bài 43 trang 132 SGK Đại số 10 nâng cao

Xác định tập nghiệm của mỗi hệ bất phương trình hai ẩn

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

Xác định tập nghiệm của mỗi hệ bất phương trình hai ẩn

LG a

\(\left\{ \matrix{
{x \over 2} + {y \over 3} - 1 > 0 \hfill \cr
2(x - 1) + {y \over 2} < 4 \hfill \cr} \right.\)

Phương pháp giải:

- Xác định miền nghiệm của mỗi bất phương trình trong hệ, gạch bỏ miền còn lại.

- Miền còn lại không bị gạch là miền nghiệm cần tìm.

Lời giải chi tiết:

Hệ đã cho tương đương với hệ:

\(\left\{ \matrix{
3x + 2y - 6 > 0 \hfill \cr
4x + y - 12 < 0 \hfill \cr} \right.\)

Vẽ các đường thẳng 3x + 2y - 6 = 0 và 4x + y - 12 = 0.

Xét điểm O(0;0) không thuộc cả hai đường thẳng trên ta thấy:

\(\left\{ \begin{array}{l}
3.0 + 2.0 - 6 < 0\\
4.0 + 0 - 12 < 0
\end{array} \right.\) nên O thuộc miền nghiệm của bpt thứ hai nhưng không thuộc miền nghiệm của bpt thứ nhất.

Miền nghiệm của hệ là miền không bị gạch chéo (không kể biên) như hình vẽ:

LG b

\(\left\{ \matrix{
4x - 5y + 20 > 0 \hfill \cr
y > 0 \hfill \cr
- y + 5 > {{x - 3} \over 3} \hfill \cr} \right.\)

Phương pháp giải:

- Xác định miền nghiệm của mỗi bất phương trình trong hệ, gạch bỏ miền còn lại.

- Miền còn lại không bị gạch là miền nghiệm cần tìm.

Lời giải chi tiết:

Hệ đã cho tương đương với hệ:

\(\left\{ \matrix{
4x - 5y + 20 > 0 \hfill \cr
y > 0 \hfill \cr
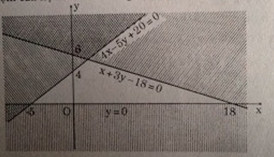
x + 3y - 18 < 0 \hfill \cr} \right.\)

Miền nghiệm của hệ là miền không bị gạch (không kể biên) trên hình.

Loigiaihay.com

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 11 phiếu

Bài tiếp theo

Bài 44 trang 132 SGK Đại số 10 nâng cao
Viết các phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi biểu diễn hình học miền nghiệm (S) của hệ đó.
Bài 45 trang 135 SGK Đại số 10 nâng cao
Xác định miền nghiệm của các hệ bất phương trình hai ẩn
Bài 46 trang 135 SGK Đại số 10 nâng cao
Xác định miền nghiệm của các hệ bất phương trình hai ẩn
Bài 47 trang 135 SGK Đại số 10 nâng cao
Gọi (S) là tập hợp các điểm trong mặt phẳng tọa độ có tọa độ thỏa mãn hệ:
Bài 48 trang 135 SGK Đại số 10 nâng cao
Bài toán vitamin.
Bài 42 trang 132 SGK Đại số 10 nâng cao
Xác định miền nghiệm của mỗi bất phương trình hai ẩn